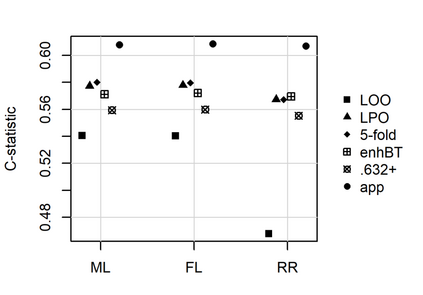
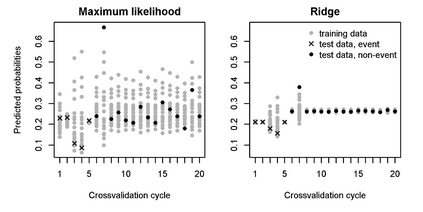
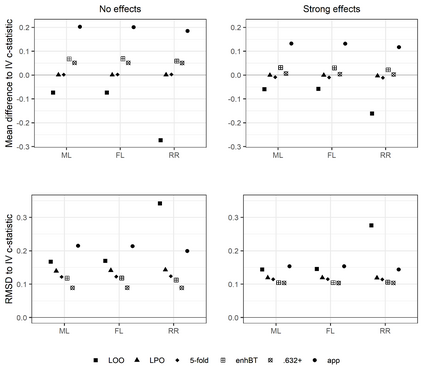
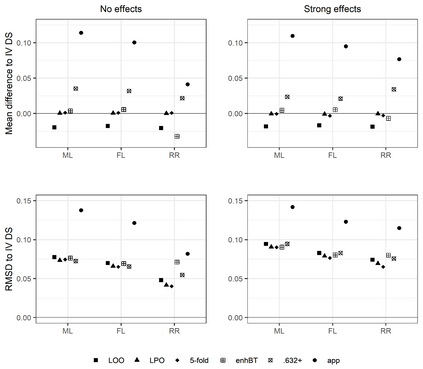
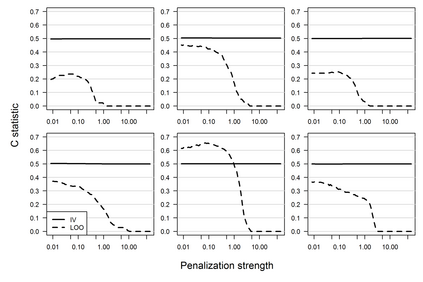
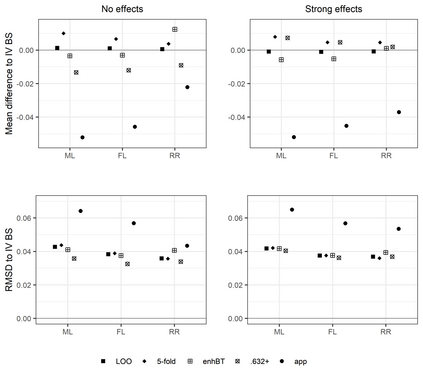
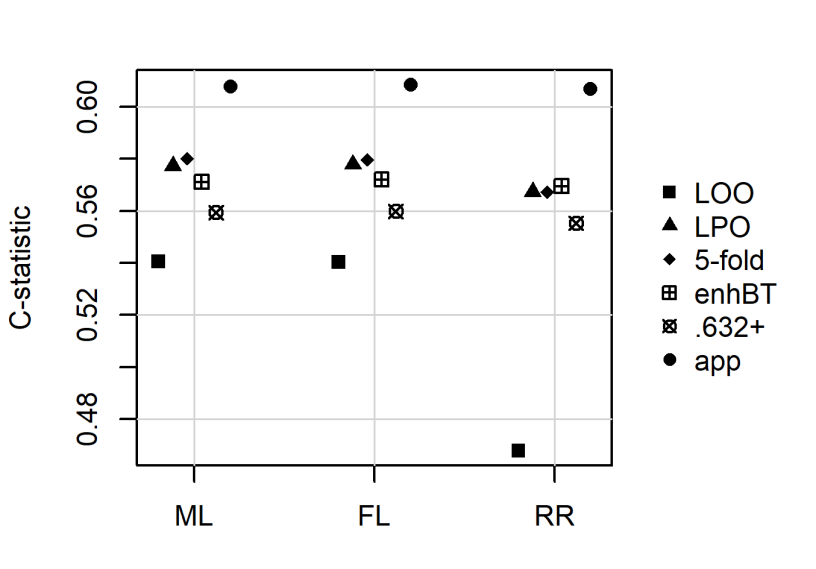
Penalized logistic regression methods are frequently used to investigate the relationship between a binary outcome and a set of explanatory variables. The model performance can be assessed by measures such as the concordance statistic (c-statistic), the discrimination slope and the Brier score. Often, data resampling techniques, e.g. crossvalidation, are employed to correct for optimism in these model performance criteria. Especially with small samples or a rare binary outcome variable, leave-one-out crossvalidation is a popular choice. Using simulations and a real data example, we compared the effect of different resampling techniques on the estimation of c-statistics, discrimination slopes and Brier scores for three estimators of logistic regression models, including the maximum likelihood and two maximum penalized-likelihood estimators. Our simulation study confirms earlier studies reporting that leave-one-out crossvalidated c-statistics can be strongly biased towards zero. In addition, our study reveals that this bias is more pronounced for estimators shrinking predicted probabilities towards the observed event rate, such as ridge regression. Leave-one-out crossvalidation also provided pessimistic estimates of the discrimination slope but nearly unbiased estimates of the Brier score. We recommend to use leave-pair-out crossvalidation, five-fold crossvalidation with repetition, the enhanced or the .632+ bootstrap to estimate c-statistics and leave-pair-out or five-fold crossvalidation to estimate discrimination slopes.
翻译:经常使用惩罚性后勤回归方法来调查二进制结果与一组解释性变量之间的关系。模型性能可以通过协调性统计(c-统计性)、差别斜坡和布里尔分数等措施进行评估。通常,数据再抽样技术(例如交叉校准)被用来纠正这些模型性能标准的乐观性。特别是用少量样本或罕见的二进制结果变量,请假一次交叉校验是一种流行的选择。使用模拟和真实数据实例,我们比较了不同再抽样技术对三进制统计统计、歧视斜度和布里尔分数估算的影响,包括最高可能性和两种最高惩罚性类似性估量。我们的模拟研究证实了先前的研究表明,请假一次一次交叉校验的C-S-S-S-xxxxx结果可能会严重偏向零倾斜。此外,我们的研究显示,这种偏差更明显地表现于预测性递减观察到的事件率,例如峰值后回归、一次歧视斜度和五年级递增性递增性递增性压性压性压性估算。