Maximum Likelihood Estimation for a Markov-Modulated Jump-Diffusion Model

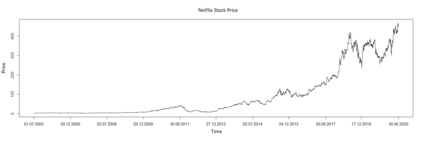
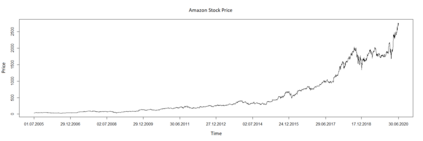
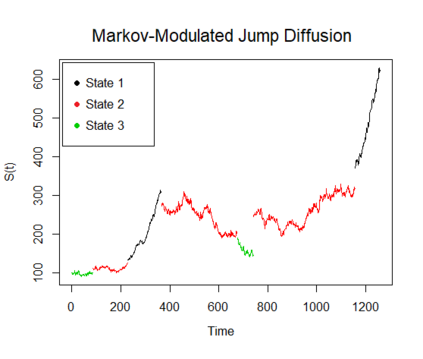
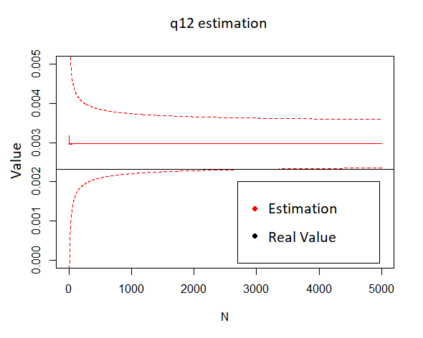
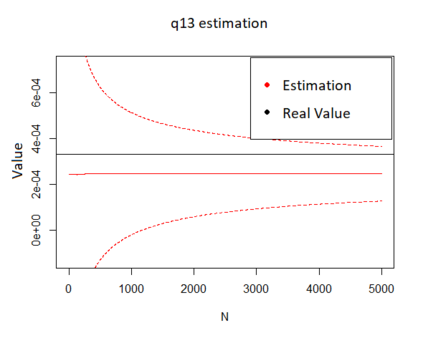
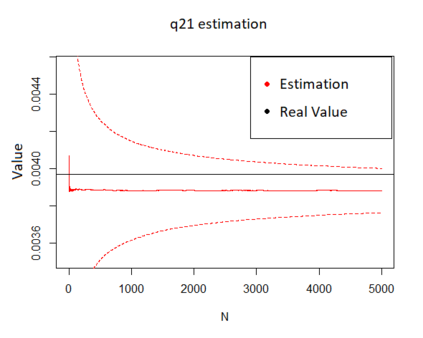
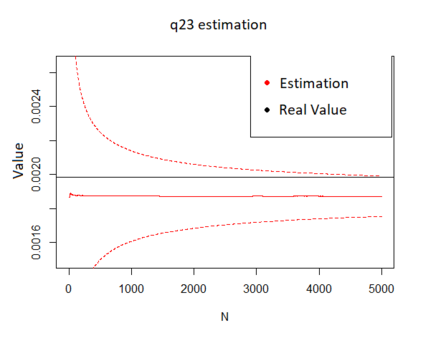
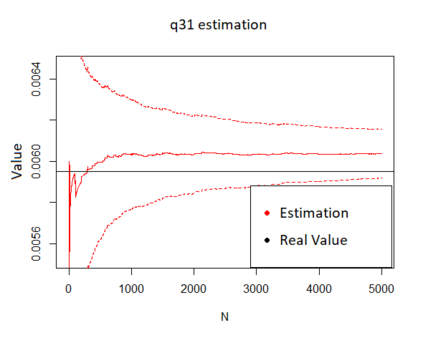
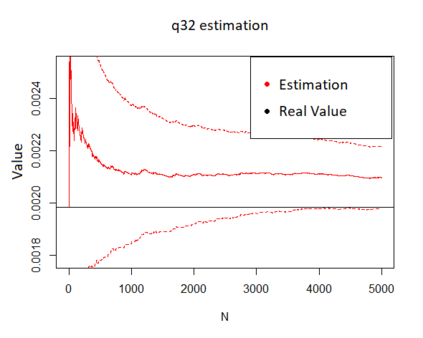
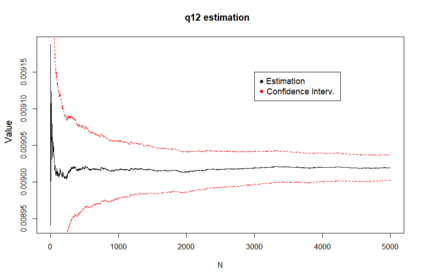
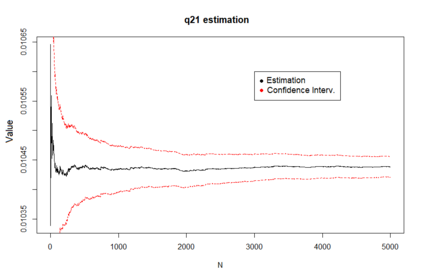
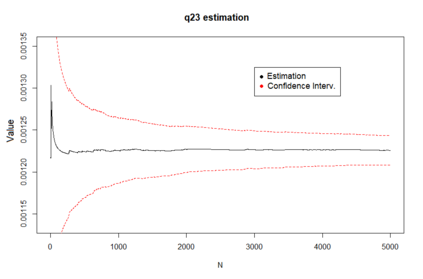
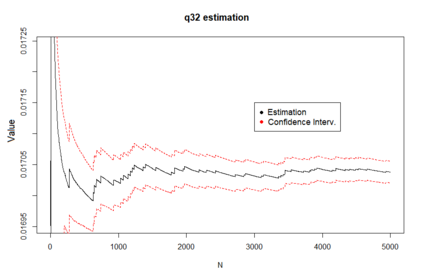
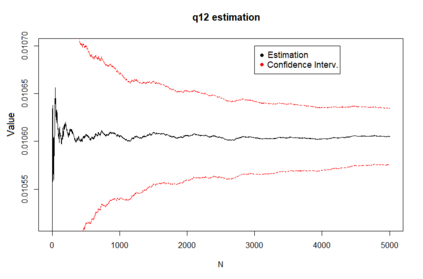
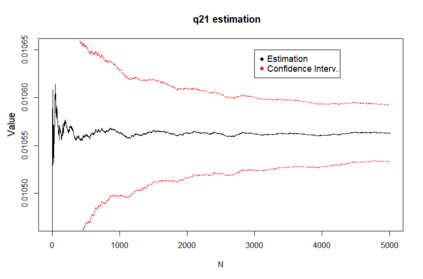
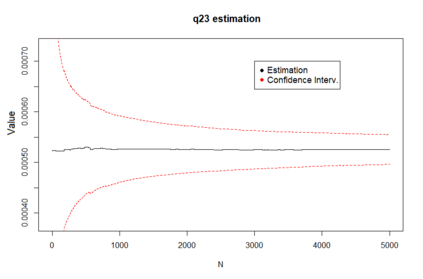
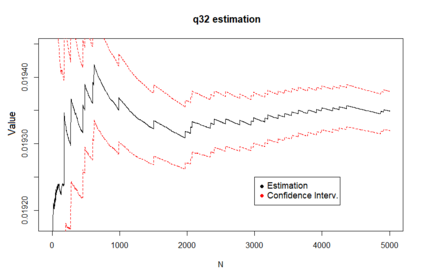
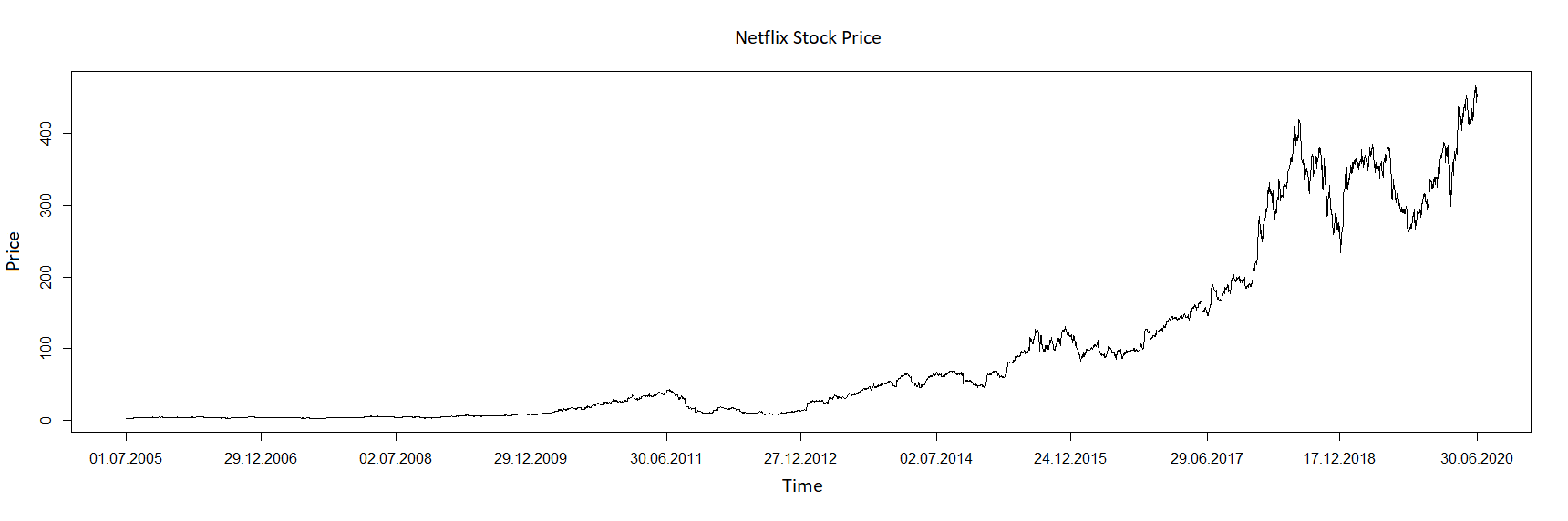
We propose a method for obtaining maximum likelihood estimates (MLEs) of a Markov-Modulated Jump-Diffusion Model (MMJDM) when the data is a discrete time sample of the diffusion process, the jumps follow a Laplace distribution, and the parameters of the diffusion are controlled by a Markov Jump Process (MJP). The data can be viewed as incomplete observation of a model with a tractable likelihood function. Therefore we use the EM-algorithm to obtain MLEs of the parameters. We validate our method with simulated data. The motivation for obtaining estimates of this model is that stock prices have distinct drift and volatility at distinct periods of time. The assumption is that these phases are modulated by macroeconomic environments whose changes are given by discontinuities or jumps in prices. This model improves on the stock prices representation of classical models such as the model of Black and Scholes or Merton's Jump-Diffusion Model (JDM). We fit the model to the stock prices of Amazon and Netflix during a 15-years period and use our method to estimate the MLEs.