On the Optimality of Treating Inter-Cell Interference as Noise in Uplink Cellular Networks

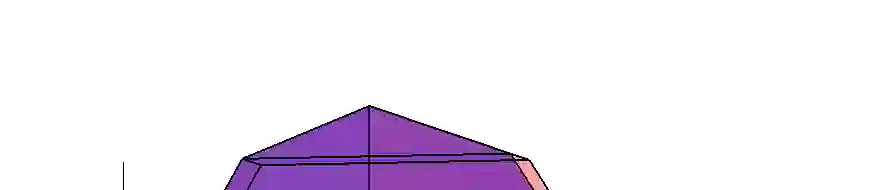
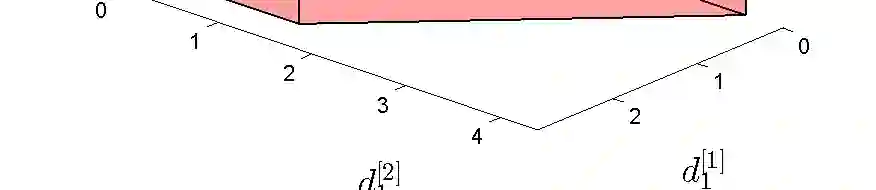
In this paper, we explore the optimality of treating interference as noise (TIN) in cellular networks. We focus on uplink scenarios modeled by the Gaussian interfering multiple access channel (IMAC), comprising $K$ mutually interfering multiple access channels (MACs), each formed by an arbitrary number of transmitters communicating independent messages to one receiver. We define TIN for this setting as a scheme in which each MAC (or cell) performs a power-controlled version of its capacity-achieving strategy, with Gaussian codebooks and successive decoding, while treating interference from all other MACs (i.e. inter-cell interference) as noise. We characterize the generalized degrees-of-freedom (GDoF) region achieved through the proposed TIN scheme, and then identify conditions under which this achievable region is a polyhedron (and hence convex) without the need for time-sharing. We then tighten these polyhedrality conditions and identify a regime in which the proposed TIN scheme achieves the entire GDoF region of the IMAC and is within a constant gap of the entire capacity region.