通过代码学Sutton强化学习第四章动态规划
经典教材Reinforcement Learning: An Introduction 第二版由强化领域权威Richard S. Sutton 和 Andrew G. Barto 完成编写,内容深入浅出,非常适合初学者。本篇详细讲解第四章动态规划算法,我们会通过Grid World示例来结合强化学习核心概念,用python代码实现在OpenAI Gym的模拟环境中第四章基于动态规划的算法:策略评价(Policy Evaluation)、策略提升(Policy Improvment)、策略迭代(Policy Iteration)、值迭代(Value Iteration)和异步迭代方法(Asynchronous DP)。
Grid World 问题
Finite MDP 模型
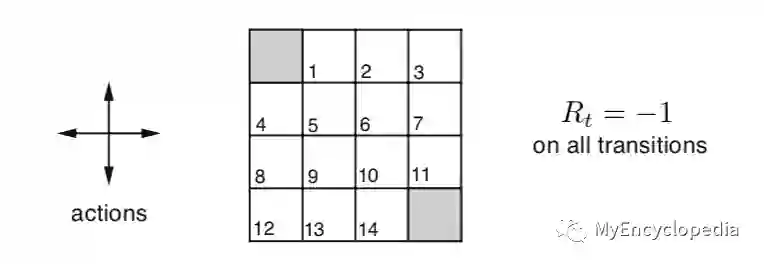
先来回顾一下强化学习的建模基础:有限马尔可夫决策过程(Finite Markov Decision Process, Finite MDP)。如下图,强化学习模型将世界抽象成两个实体,强化学习解决目标的主体Agent和其他外部环境。它们之间的交互过程遵从有限马尔可夫决策过程:若Agent在t时间步骤时处于状态 ,采取动作 ,然后环境根据自身机制,产生Reward 并将Agent状态变为 。
数学上dynamics可以如下表示
满足
以Grid World为例,当Agent处于编号1的网格时,可以往四个方向走,往任意方向走都只产生一种 S, R,因为这个简单的游戏是确定性的,不存在某一动作导致stochastic状态。例如,在1号网格往左就到了终点网格(编号0),得到Reward -1这个规则可以如下表示
因此,状态s=1的所有dynamics概率映射为
强化学习的目的
在给定了问题以及定义了强化学习的模型之后,强化学习的目的当然是通过学习让Agent能够学到最佳策略 ,也就是在某个状态下的行动分布,记成 。对应在数值上的优化目标是Agent在一系列过程中采取某种策略的reward总和的期望(Expected Return)。下面公式定义了t步往后的reward总和,其中 为discount factor,用于权衡短期和长期reward对于当前Agent的效用影响。等式最后一步的意义是t步后的reward总和等价于t步所获的立即reward ,加上t+1步后的reward总和 。
下面公式推导了 数值上和相关状态 的关系:
注意到如果将 看成未知数,上式即形成 个未知变量的方程组,可以在数值上解得各个 。
书中用Backup Diagram来表示递推关系,下图是 的backup diagram。
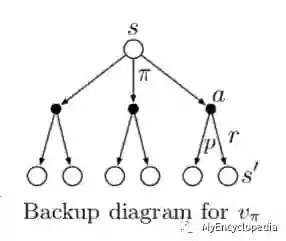
尽管v值可以来衡量策略,但由于 是Agent在策略 的Expected Return,将不同的action拆出来单独计算Expected Return,这样的做法有时更为直接,这就是著名的Q Learning中的q 值,记成 。
下面是 的递推 backup diagram。
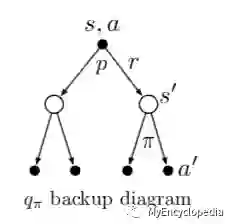
Bellman 最佳原则
对于所有状态集合 ,策略 的评价指标 是一个向量,本质上是无法相互比较的。但由于存在Bellman 最佳原则(Bellman's principle of optimality):在有限状态情况下,一定存在一个或者多个最好的策略 ,它在所有状态下的v值都是最好的,即 。
因此,最佳v值定义为最佳策略 对应的 v 值
同理,也存在最佳q值,记为
将 改写成递推形式,称为 Bellman Optimality Equation,推导如下
直觉上可以理解为状态 s 对应的最佳v值是只采取此状态下的最佳动作后的Expected Return。
最佳q值递归形式的意义为最佳策略下状态s时采取行动 a 的Expected Return,等于所有可能后续状态 s' 下采取最优行动的Expected Return的均值。推导如下:
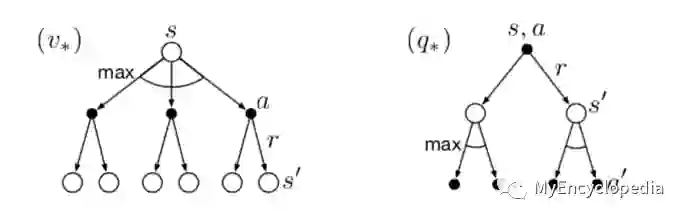
的backup diagram 如下图
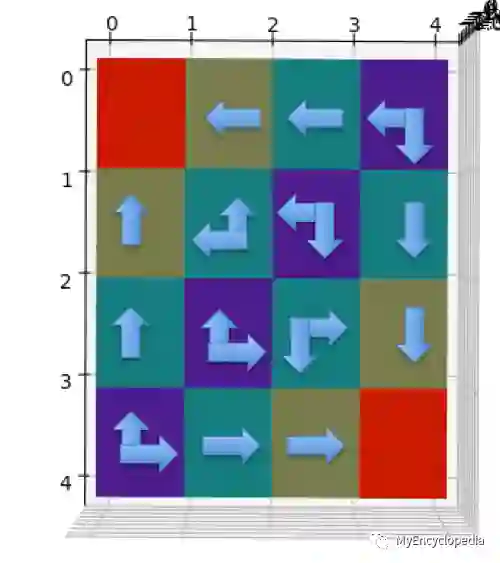
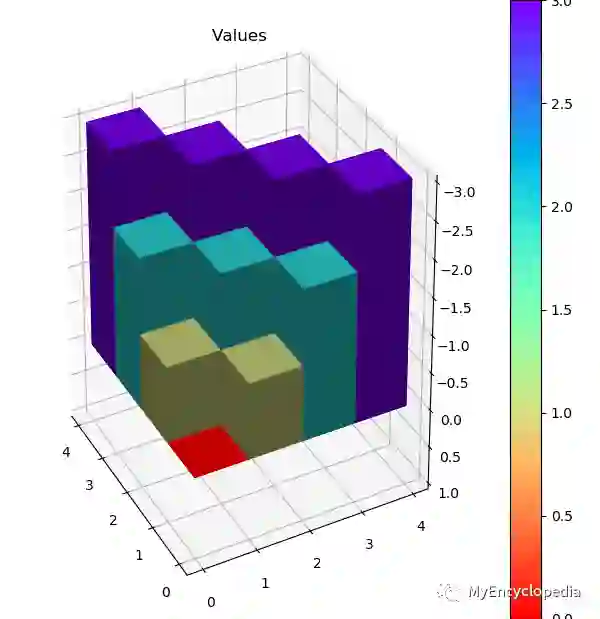
Grid World 最佳策略和V值
Grid World 的最佳策略如下:尽可能快的走出去
Grid World OpenAI Gym 环境
下面是OpenAI Gym框架下Grid World环境的代码实现。本质是在GridWorldEnv构造函数中构建MDP,类型定义如下
MDP = Dict[State, Dict[Action, List[Tuple[Prob, State, Reward, bool]]]]
# P[state][action] = [
# (prob1, next_state1, reward1, is_done),
# (prob2, next_state2, reward2, is_done), ...]
class Action(Enum):
UP = 0
DOWN = 1
LEFT = 2
RIGHT = 3
State = int
Reward = float
Prob = float
Policy = Dict[State, Dict[Action, Prob]]
Value = List[float]
StateSet = Set[int]
NonTerminalStateSet = Set[int]
MDP = Dict[State, Dict[Action, List[Tuple[Prob, State, Reward, bool]]]]
# P[s][a] = [(prob, next_state, reward, is_done), ...]
class GridWorldEnv(discrete.DiscreteEnv):
"""
Grid World environment described in Sutton and Barto Reinforcement Learning 2nd, chapter 4.
"""
def __init__(self, shape=[4,4]):
self.shape = shape
nS = np.prod(shape)
nA = len(list(Action))
MAX_R = shape[0]
MAX_C = shape[1]
self.grid = np.arange(nS).reshape(shape)
isd = np.ones(nS) / nS
# P[s][a] = [(prob, next_state, reward, is_done), ...]
P: MDP = {}
action_delta = {Action.UP: (-1, 0), Action.DOWN: (1, 0), Action.LEFT: (0, -1), Action.RIGHT: (0, 1)}
for s in range(0, MAX_R * MAX_C):
P[s] = {a.value : [] for a in list(Action)}
is_terminal = self.is_terminal(s)
if is_terminal:
for a in list(Action):
P[s][a.value] = [(1.0, s, 0, True)]
else:
r = s // MAX_R
c = s % MAX_R
for a in list(Action):
neighbor_r = min(MAX_R-1, max(0, r + action_delta[a][0]))
neighbor_c = min(MAX_C-1, max(0, c + action_delta[a][1]))
s_ = neighbor_r * MAX_R + neighbor_c
P[s][a.value] = [(1.0, s_, -1, False)]
super(GridWorldEnv, self).__init__(nS, nA, P, isd)
4.1 策略评估(Policy Evaluation)
策略评估需要解决在给定环境dynamics和Agent策略 下,计算策略的v值 。由于所有数量关系都已知,可以通过解方程组的方式求得,但通常会通过数值迭代的方式来计算,即通过一系列 收敛至 。如下迭代方式已经得到证明,当 一定收敛至 。
书中具体伪代码如下
下面是python 代码实现,注意这里单run迭代时,新的v值直接覆盖数组里的旧v值,这种做法在书中被证明不仅有效,甚至更为高效。这种做法称为原地(in place)更新。
def policy_evaluate(policy: Policy, env: GridWorldEnv, gamma=1.0, theta=0.0001):
V = np.zeros(env.nS)
while True:
delta = 0
for s in range(env.nS):
v = 0
for a, action_prob in enumerate(policy[s]):
for prob, next_state, reward, done in env.P[s][a]:
v += action_prob * prob * (reward + gamma * V[next_state])
delta = max(delta, np.abs(v - V[s]))
V[s] = v
if delta < theta:
break
return np.array(V)
输入策略为随机选择方向,运行上面的policy_evaluate最终多轮收敛后的V值输出为
[[ 0. -13.99931242 -19.99901152 -21.99891199]
[-13.99931242 -17.99915625 -19.99908389 -19.99909436]
[-19.99901152 -19.99908389 -17.99922697 -13.99942284]
[-21.99891199 -19.99909436 -13.99942284 0. ]]
在3D V值图中可以发现,由于是随机选择方向的策略, Agent在每个格子的V值绝对数值要比最佳V值大,意味着随机策略下Agent在Grid World会得到更多的负reward。
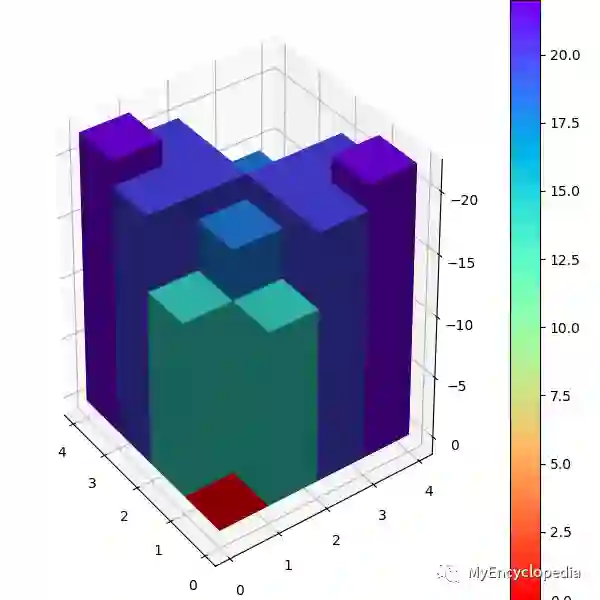
4.2 策略迭代
上一篇中,我们知道如何evaluate 给定policy 的 值,那么是否可能在此基础上改进生成更好的策略 。如果可以,能否最终找到最佳策略 ?答案是肯定的,因为存在策略提升定理(Policy Improvement Theorem)。
策略提升定理
在 4.2 节 Policy Improvement Theorem 可以证明,利用 信息对于每个状态采取最 greedy 的 action (又称exploitation)能够保证生成的新 是不差于旧的policy ,即
因此,可以通过在当前policy求得v值,再选取最greedy action的方式形成如下迭代,就能够不断逼近最佳策略。
4.3 策略迭代算法
以下为书中4.3的policy iteration伪代码。其中policy evaluation的算法在上一篇中已经实现。Policy improvement 的精髓在于一次遍历所有状态后,通过policy 的最大Q值找到该状态的最佳action,并更新成最新policy,循环直至没有 action 变更。
Q值函数实现如下:
def action_value(env: GridWorldEnv, state: State, V: StateValue, gamma=1.0) -> ActionValue:
q = np.zeros(env.nA)
for a in range(env.nA):
for prob, next_state, reward, done in env.P[state][a]:
q[a] += prob * (reward + gamma * V[next_state])
return q
有了 action_value 和上期的 policy_evaluate,policy iteration 实现完全对应上面的伪代码。
def policy_improvement(env: GridWorldEnv, policy: Policy, V: StateValue, gamma=1.0) -> bool:
policy_stable = True
for s in range(env.nS):
old_action = np.argmax(policy[s])
Q_s = action_value(env, s, V)
best_action = np.argmax(Q_s)
policy[s] = np.eye(env.nA)[best_action]
if old_action != best_action:
policy_stable = False
return policy_stable
def policy_iteration(env: GridWorldEnv, policy: Policy, gamma=1.0) -> Tuple[Policy, StateValue]:
iter = 0
while True:
V = policy_evaluate(policy, env, gamma)
policy_stable = policy_improvement(env, policy, V)
iter += 1
if policy_stable:
return policy, V
Grid World 例子通过两轮迭代就可以收敛,以下是初始时随机策略的V值和第一次迭代后的V值。
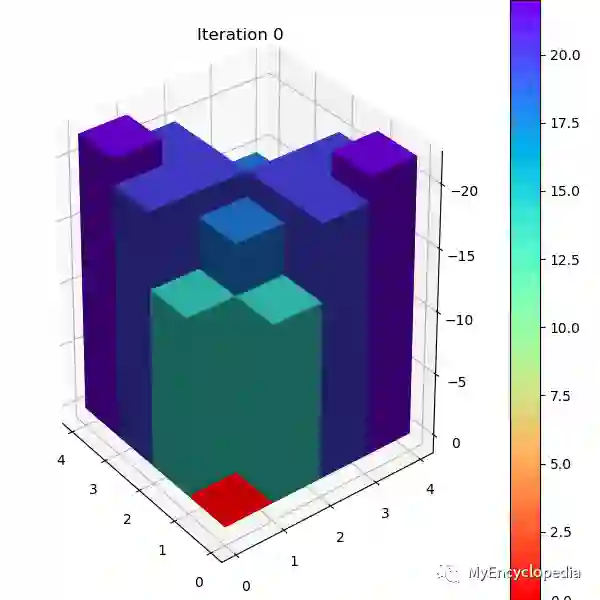
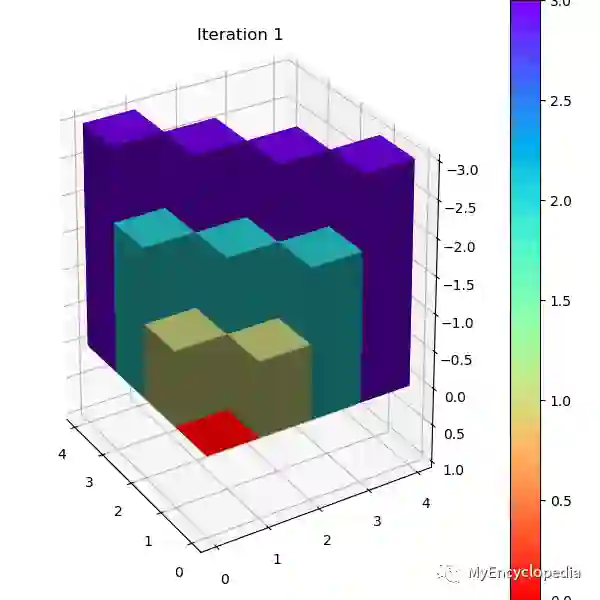
4.4 值迭代
值迭代( Value Iteration)的本质是,将policy iteration中的policy evaluation过程从不断循环到收敛直至小于theta,改成只执行一遍,并直接用最佳Q值更新到状态V值,如此可以不用显示地算出 而直接在V值上迭代。具体迭代公式如下:
代码实现也比较直接,可以复用上面已经实现的 action_value 函数。
def value_iteration(env:GridWorldEnv, gamma=1.0, theta=0.0001) -> Tuple[Policy, StateValue]:
V = np.zeros(env.nS)
while True:
delta = 0
for s in range(env.nS):
action_values = action_value(env, s, V, gamma=gamma)
best_action_value = np.max(action_values)
delta = max(delta, np.abs(best_action_value - V[s]))
V[s] = best_action_value
if delta < theta:
break
policy = np.zeros([env.nS, env.nA])
for s in range(env.nS):
action_values = action_value(env, s, V, gamma=gamma)
best_action = np.argmax(action_values)
policy[s, best_action] = 1.0
return policy, V
4.5 异步迭代
在第4.5节中提到了DP迭代方式的改进版:异步方式迭代(Asychronous Iteration)。这里的异步是指每一轮无需全部扫一遍所有状态,而是根据上一轮变化的状态决定下一轮需要最多计算的状态数,类似于Dijkstra最短路径算法中用 heap 来维护更新节点集合,减少运算量。下面我们通过异步值迭代来演示异步迭代的工作方式。
下图表示状态的变化方向,若上一轮 发生更新,那么下一轮就要考虑状态 s 可能会影响到上游状态的集合( p1,p2),避免下一轮必须遍历所有状态的V值计算。
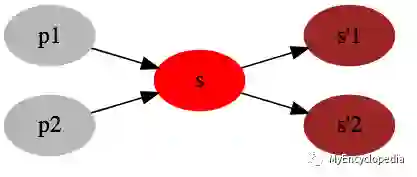
建立映射关系的代码如下,build_reverse_mapping 返回类型为 Dict[State, Set[State]]。
def build_reverse_mapping(env:GridWorldEnv) -> Dict[State, Set[State]]:
MAX_R, MAX_C = env.shape[0], env.shape[1]
mapping = {s: set() for s in range(0, MAX_R * MAX_C)}
action_delta = {Action.UP: (-1, 0), Action.DOWN: (1, 0), Action.LEFT: (0, -1), Action.RIGHT: (0, 1)}
for s in range(0, MAX_R * MAX_C):
r = s // MAX_R
c = s % MAX_R
for a in list(Action):
neighbor_r = min(MAX_R - 1, max(0, r + action_delta[a][0]))
neighbor_c = min(MAX_C - 1, max(0, c + action_delta[a][1]))
s_ = neighbor_r * MAX_R + neighbor_c
mapping[s_].add(s)
return mapping
有了描述状态依赖的映射 dict 后,代码也比较简洁,changed_state_set 变量保存了这轮必须计算的状态集合。新的一轮迭代时,将下一轮需要计算的状态保存到 changed_state_set_ 中,本轮结束后,changed_state_set 更新成changed_state_set_,开始下一轮循环直至没有状态需要更新。
def value_iteration_async(env:GridWorldEnv, gamma=1.0, theta=0.0001) -> Tuple[Policy, StateValue]:
mapping = build_reverse_mapping(env)
V = np.zeros(env.nS)
changed_state_set = set(s for s in range(env.nS))
iter = 0
while len(changed_state_set) > 0:
changed_state_set_ = set()
for s in changed_state_set:
action_values = action_value(env, s, V, gamma=gamma)
best_action_value = np.max(action_values)
v_diff = np.abs(best_action_value - V[s])
if v_diff > theta:
changed_state_set_.update(mapping[s])
V[s] = best_action_value
changed_state_set = changed_state_set_
iter += 1
policy = np.zeros([env.nS, env.nA])
for s in range(env.nS):
action_values = action_value(env, s, V, gamma=gamma)
best_action = np.argmax(action_values)
policy[s, best_action] = 1.0
return policy, V
比较值迭代和异步值迭代方法后发现,值迭代用了4次循环,每次涉及所有状态,总计算状态数为 4 x 16 = 64。异步值迭代也用了4次循环,但是总计更新了54个状态。由于Grid World 的状态数很少,异步值迭代优势并不明显,但是对于状态数众多并且迭代最终集中在少部分状态的环境下,节省的计算量还是很可观的。
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
由于微信平台算法改版,公号内容将不再以时间排序展示,如果大家想第一时间看到我们的推送,强烈建议星标我们和给我们多点点【在看】。星标具体步骤为:
(1)点击页面最上方"AINLP",进入公众号主页。
(2)点击右上角的小点点,在弹出页面点击“设为星标”,就可以啦。
感谢支持,比心

推荐阅读
征稿启示| 200元稿费+5000DBC(价值20个小时GPU算力)
完结撒花!李宏毅老师深度学习与人类语言处理课程视频及课件(附下载)
模型压缩实践系列之——bert-of-theseus,一个非常亲民的bert压缩方法
文本自动摘要任务的“不完全”心得总结番外篇——submodular函数优化
斯坦福大学NLP组Python深度学习自然语言处理工具Stanza试用
关于AINLP
AINLP 是一个有趣有AI的自然语言处理社区,专注于 AI、NLP、机器学习、深度学习、推荐算法等相关技术的分享,主题包括文本摘要、智能问答、聊天机器人、机器翻译、自动生成、知识图谱、预训练模型、推荐系统、计算广告、招聘信息、求职经验分享等,欢迎关注!加技术交流群请添加AINLPer(id:ainlper),备注工作/研究方向+加群目的。
阅读至此了,分享、点赞、在看三选一吧🙏





