“荡气回肠”!UCLA蒋陈凡夫万字长文回顾:从转系生到图形学终身教授的十二年
金磊 转载整理自 知乎
量子位 | 公众号 QbitAI
这是一篇由UCLA应用数学副教授蒋陈凡夫所撰写的万字长文,回顾了他在图形学物理模拟领域里十二年来的点点滴滴。
于人,于事,于学术,字里行间无不在透露着蒋陈凡夫对图形学的热爱与浪漫,感动了无数的网友。
在文中被他称为“少年英雄”的胡渊鸣,在看完后甚至直呼“荡气回肠”。
目前已经揽获近3000的赞。

(注:本文经授权转载,以下为原文)
最近评上tenure(终身教授),有人来祝贺:”Now you can freely decline review requests!”。我想了想,似乎对心态上的改变确实如此而已。又想到也许可以写个什么纪念一下。那这19岁到31岁,有什么拿来回味的没有?好像有很多,但不整理一下的话,又不知从何说起。那还是直接写一点吧。从物理本科,到CS PhD,CS教职,又在数学tenure,这看似曲折的十二年竟是在做同样的研究,一年都没有浪费。一路走来,有很多东西值得缅怀和总结,也许能帮助思考未来。顺便把这一路干过的牛逼的事,和遇到过的牛逼的人都写下来,看着应该很舒爽。
第〇章:我的三叉戟
第一章:缘起
第二章:一炮炸出来两个坑
第三章:雪与海的浪漫
第四章:摩擦摩擦,在光滑的路上,摩擦
第五章:少年英雄胡渊鸣
第六章:与Timestep结缘
第七章:摩擦碰撞的第三次战役,IPC魔童降世
第八章:下一个“Timestep”
第〇章:我的三叉戟
十二年来摸爬滚打地给计算机图形学做了些物理模拟相关的科研。拿的出手的代表方向有三:物质点法(Material Point Method: MPM),仿射粒子元胞法(Affine Particle In Cell: APIC),和增量势能接触法(Incremental Potential Contact: IPC)。每个方法的人和事下面的章节再去回忆,这一章,先笼统概括一下。
第一个方向:MPM。说到物质点法,按照惯例,或许得提一下自己多多少少参与了的冰雪奇缘。2012年发掘MPM后我去做了些别的事情,组里其他同学拿MPM验证了雪;我在早期没有去参与最初的SIGGRAPH工作。迪士尼工作室的代码很臃肿,远远不止99行,而且迪士尼的律师可不是吃素的,向来有荒岛求生画米奇一说。既然不能描绘太多代码的事情,那就只放好看的剧照:
MPM擅长做雪在短期内成为了一个刻板印象。于是我决定花一些功夫来重塑一下MPM的形象。从技术层面上来说,MPM只是一个基本的Galerkin空间架构,物理过程数值模拟的真正技术点在于时间和空间的离散算法、本构模型的设计、性能的加速、以及巧妙求解偏微分方程数值解的不同手段。MPM是一块高品质的画布,这些技术点的创新才是真正的笔法(stroke)。但是技术点是里子,MPM是面子。
于是从面子上看到的,便是我与一干志趣相投之士用MPM去平A物理的世界的各种固体和流体:巧克力,果冻,面包,牙膏,冰淇淋,泡沫,泥土,岩浆,牛排,东坡肉,橘子,西瓜,肌肉,骨骼,内脏,布料,毛衣,头发,雪山,沙海,冰川,河流,无人机,炸药,等等。这里有固体,有牛顿流体,有非牛顿流体,有粒状体,有固液混合体,还有人体。大到山川河流,小到雨露甘霖,MPM从一个铁头功,逐渐被扩写成了一本七十二绝技。
后来跟人合开了公司,写了一个实用的MPM特效解算器。最近Autodesk买下并放进了Maya,相信未来的几年,更多的电影里会看到MPM的应用场景。
第二个方向:仿射粒子元胞法(APIC)。这是我2015年得意的文章,是2014年的圣诞节独自一人在迪士尼的大帽子studio里加班完工的。迪士尼所在的Burbank是大洛杉矶地区一个荒漠城市,我却在荒漠和大海结了缘。于是那一年,APIC给海洋奇缘里的水提升了许多丰富的细节。
时间快进到2017年,有一位气血翻腾的胡姓少年来访问我,一起把APIC和MPM系列工作推到了高潮:Moving Least Squares MPM(MLS-MPM)。那之中与后来太极图形的渊源和MPM在可微分模拟领域的拓展,已有好文记录。
第三个方向:IPC。2020年12月31日,宾夕法尼亚大学计算机图形学中心,23点59分,手里的咖啡还烫。有一块补天的石头,它吸满了天地灵气日月精华,突然炸裂开了。增量势能接触法IPC横空出世。王婆卖瓜自卖自夸:我窃以为,IPC改良了固体模拟,启动了“工业革命”,把连续固体的仿真科学(不只在图形学)带入了“蒸汽机时代”。2022年,它的衍生故事还在不断上演:
第一章:缘起
2010年,我遇到了改变了我一生的三个人。第一个人是我的妻子;这十二年,我们相恋五年,结婚七年,她挽着我踩下了每一个有深有浅的脚印。十二年来做过的每一个回头来看无比正确的决定,大到职业道路,小到咬文嚼字,我的许多影响深远的选择背后都有她默默的付出不休不眠的时间陪我去抽丝剥茧和理性分析。
我在中科大少年班选的专业是等离子体物理,2010年在UCLA入学后想转到计算机,如果没有她绝对理性地安抚我的急躁和帮我规划合理的步骤,我可能连第一学期都没读完就自暴自弃、不知所向。她还会陪我走很远很远。
2010年改变我命运的另两个人,就是我读PhD的联合导师Demetri Terzopoulos和Joseph Teran。他们的成就是我一生奋斗的目标。
我在UCLA CS系的导师Demetri是英国皇家学会的院士(并列于牛顿、本杰明富兰克林、霍金等人),奥斯卡技术奖得主,他是1980年代计算机图形学里第一个做物理仿真的人,可谓元宇宙物理引擎之父。他同时也是计算机视觉泰斗,发明了snake算法。他其实还跟Hinton一起在二十多年前就发表了世界上第一篇用神经网络做物理仿真的图形学文章,似乎常常被人漏cite。
我在数学系的共同导师是Joseph,他是陶哲轩的同事(我现在也是了),Level Set发明人Stan Osher的徒孙和同事,曾被discover评为40岁以下最聪明的20个大脑之一(20 Best Brains Under 40),他是图形学里最有名的做有限元固体仿真的人。
2010年秋天,我跟一个朋友一起联系了Demetri,以及Joseph和朱松纯老师。朱老师给出了很理性的不赞成我转系的答复。(后来朱老师对我改观,跟Osher一起加入了我的博士委员会,再后来通过挚友,如今北大智能学院的朱毅鑫教授,形成密切的学术合作关系,这是后话)。
Demetri和Joseph冒着很大的实验室财务浪费的风险,看着我一段蹩脚的弹簧模拟代码(MATLAB写的),但是考虑到我以前发表过相对论相关的论文应该脑子不笨,给了我一个机会。我赶紧红牛下肚,花了几个通宵强行通读了一本教材,并复现出了一篇有限元肌肉仿真的siggraph文章。诸如此行为,是impress图形学教授最简洁有效的手段。从此一发不可收拾。
写代码和图形学,我入门都很迟。胡渊鸣初中就写刚体引擎小游戏了,我博一还在自学C++模板。跟许多有理想的图形学或游戏爱好者一样,从头搭建一个自己的引擎是一个抑制不住的冲动。2012年初,补完所有计算机和应用数学课程的我结合自己的物理背景,摸索出了一个长期目标:用物理仿真去重建这个世界。
Demetri也鼓励我:你比谁都适合去close the gap between virtual reality and physical reality, 把虚拟世界跟物理世界给打通。那时候没有元宇宙这个说法,但是我的两个导师都是digital double虚拟人体的深度发烧友,这对我的科研兴趣的影响不可谓不大。回到物理引擎这个构想上,心动不如行动,这世界五颜六色千变万化,那这引擎就叫魔方大,哦不,百变怪吧!于是ditto诞生了:
ditto里包含了几个固体仿真和碰撞处理的练手项目,特别是隐式有限元的3D布料仿真。当时有taichi语言的话,应该写出来能当一次GAMES201大作业拿个A+。
可惜Ditto维持了半年后,我投入一篇siggraph文章的具体工作中,便没有再更新了。后来2018年z-emotion/ZelusFX公司的CEO突然联系我,说他2012年跟我要的ditto代码帮助他弄出来一个布料设计软件的公司,现在有很多用户。我开心了很久。
第二章:一炮炸出来两个坑
我博士期间花了两年时间合作的第一个项目,是物体破碎。网上有人说,计算机图形学是程序员的三大浪漫之一(另两个是操作系统和编译原理),但那时的我还没有看到浪漫,只看到了狂拽炫酷,只想在siggraph上播最帅的demo,做最靓的仔。
那时我学完了计算固体力学。跟许多做仿真的初学者一样,一切都是从模拟果冻开始,毕竟果冻是最典型的弹性体,并且往往很软,不会给ODE(常微分方程)的时间步离散格式带来过分stiff从而要么dt小,要么系统难解的这个数值问题。于是在弹塑性固体里面,我找到一个想要模拟的案例:子弹射穿果冻。那时乃至今日看来,都没有多少比这更炫酷的实拍视频:
现在教职期间,我常告诉自己的学生,想做什么科研,在大致调研相关工作并确定学术品位和潜在影响力之后,可以直接开始撸代码,不要太担心techinical contribution不够。因为你开始做之后,很快就会遇到你之前多半没预料到的问题,解决它们将成为你文章的最主要contribution。
我们用有限元去写果冻破碎,不到半个月,就碰到了两个重大的难题:(1)如何自然破裂,即不能在裂面看到三角形丑陋的样子,和(2)如何稳健地处理复杂碎片之间的摩擦碰撞。
拓扑变化哪家强,Level Set敢称王。要实现自然破裂,结合有限元和level set方法是一个非常巧妙的思路。Level Set有非常强的灵活性,可以从各种自然的角度去分裂四面体,而且可以完全避免重新划分网格(remesh)。
Level Set方法的发明人Stan Osher在UCLA,给了我们一些宝贵的建议,很快,破裂的问题便迎刃而解了。
这篇文章,我更主要负责的是做摩擦碰撞。建模破裂之后,这顺其次成为最头疼的事情。Level Set的marching tetrahedra切割法带来了无数形状“恶心”的果冻碎片:在裂面上,有的三角形瘦如一道闪电,有的扁如一张大饼。计算几何上,这些奇特的三角形被称作是“ill conditioning”,想要用普通几何方法去搞定它们的碰撞,不说碰撞算法本身的case难以穷举,光是浮点数精度带来的千变万化的误判就足以让人望洋兴叹。我花一年时间试了很多算法,皆以宣告失败。
最值得讲的一个算法,是一个非常大胆的idea。我把解算完的固体投射到一个规则的网格上,然后让网格假装看到的是不可压流体,求解一个泊松方程,把速度场变成无散的,再插值回到固体上。这竟给出了非常漂亮的不穿透解!但是缺点在于,物体的运动被变的太像流体一般轻盈灵动了,缺少了那份固体特有的执拗。我便去问我的导师Joseph,有没有类似于这个解流体方法的解固体的方法,我想拿来在碰撞上试一试。他回忆良久,说出了我一个我随后持续专注十年的名称:MPM。
MPM是1995年在美国的国家实验室发明的。它是一个混合拉格朗日粒子和欧拉网格的固体解算方法。往前追溯到1960年代的Particle-In-Cell(PIC法,最初用于求解等离子体物理的麦克斯韦方程)和1980年代的Fluid-Implicit-Particle-Method (FLIP法,用于流体结算,张心欣的导师Robert Bridson,我的师叔,于2005年引入图形学)。它像流体一样,自动防止了材料间的穿透,又可以漂亮地求解固体的方程。把MPM拿过来做碰撞处理,在当时的我看来,再合适不过了:
终于,我交了一份目前回头看来远远不够完美的答卷:
这颗子弹大的有点夸张,更像一枚炮弹。它被评为了SCA 2013的Best Paper Award。它也炸开来两个MPM带来的学术大坑:拓扑变化的多材料,和自动处理的摩擦碰撞。我和MPM被凑到了一起,从暧昧到沉迷。
彩蛋:文章里还首次用刑了一只犰狳,引起了许多论文读者的不适。但后来这个场景,竟多次被别的研究者作为benchmark来follow,那可不怪我咯。
第三章:雪与海的浪漫
学习MPM的那几个月,同组的俄国师兄Alexey也加入到粉丝小分队中来,并主导了广为流传的“MPM snow”的那篇文章。一时间,我们组和迪士尼的联姻传为佳话。有我在内的好几个学生去迪士尼实习和参与写作Production软件代码。在冰雪奇缘的庆功宴上,我第一次尝到技术产业化的喜悦。
冰雪奇缘之后,迪士尼做了一个Big Hero 6超能陆战队。在那里,MPM被用在模拟一些奇怪的材料上,这是个未怎么宣传过的信息。
△Disney's Big Hero 6
时间随之转移到2014年。我打算博士毕业了,想做一些在MPM和PIC里面更数学更基础的东西,又同时希望能在现有的FLIP流体和MPM固体上做出有应用价值的变革。那么回顾一下,用FLIP做流体,和用MPM做固体,流程中的数学上有什么不合理的hack呢?内行人一定会指出:是FLIP-PIC blending ratio。FLIP和PIC其实可以指代混合粒子网格法中,网格向粒子插值的那个步骤。
PIC直接做速度场的插值,但是会引入巨大的数值粘性,FLIP插值速度增量,但是会引入巨大的不稳定性。于是图形学的流体泰斗Robert Bridson教授在2005年就提出,把FLIP的结果乘以0.97,再把PIC的结果乘以0.03,然后把它们加起来。这个数字是一个用户可调的参数,但可调而不可控!不同的场景下,不同数字会给出非常不同的结果。它是艺术家的噩梦,是强迫症的地狱。
于是我决定干一票大的,把这个东西除掉,因为我有一个信念:需要设置heuristic参数的仿真算法绝不可能是一个好算法的最终形态。
再结合对于角动量守恒方程的理论分析,跳过一些技术细节,Affine Particle In Cell (APIC)被误打误撞推导了出来。FLIP流体和MPM固体进入了一个新的篇章,艺术家们可以更轻松的得到它们需要的仿真结果粘稠度,无论是山川大河,还是岩浆滚滚。它们在我心中,是可以媲美冰雪的浪漫。
迪士尼非常高兴,迫不及待地把APIC用进了海洋奇缘:
2015年夏天,我毕业和结婚。婚礼在洛杉矶南边的玻璃大教堂,有山有海有树林。那年暑假的SIGGRAPH,我认识了很多很多志同道合的朋友。印象最深的是在流体的session上,我看到一位风流倜傥的银发少年。他跑来问我,“今年的好文章众多,能长久流传的是哪几个?”我随便应付了几句。他说道:“今年的文章,有两篇最diao,一篇是我的IVOCK,另一篇是你的APIC。”
我吃了一惊,连忙互换姓名。原来这位霸气的少年,叫张心欣,他现在带领“泽森科工”在为中国特效打天下。那时纯粹的我们,在对方双眸反光里,都看到了一个勇者,持各自打造的巨剑,浴血挑战着一头叫做数值耗散的恶龙。自那天起,我们也开始了迄今长达七年的并肩合作。
毕业之后,我继续深耕MPM固体和流体。学术界的人其实蛮喜欢立flag。我就一直尽量坚持去贯彻一个基本原则:即使我的仿真文章是投在图形学会议和期刊上,我也绝不为了视觉效果去做任何不符合物理和数学原理的hack;我需要每个算法都普适到整个计算物理学。这个原则给后来教授期间的我带来了很多的好处:包括了(1)自然科学研究基金的青睐,(2) 在Nature子刊发表的MPM自然灾害预测技术(雪崩,山体滑坡,泥石流,冰川碎裂,海啸):

以及(3)医院十分喜爱的虚拟创伤和手术的仿真平台:
它们也许没有雪与海一样浪漫,但却更加真实和直接地影响到了这个世界,甚至帮忙拯救生命。这些工作也给图形学里做物理仿真的同行在自然科学和医学领域赢得了更多的尊重,纠正这些别的领域的人关于图形学就是不断引入他们做的东西的误解。
毕竟很多图形学论文喜欢把这个叫作contribution:“We introduce the XXX method to computer graphics.” 我想做的,是要物理学和数学的人发论文说同样的这句话,但是把“to”改成“from”。最近遇到的一位做经典力学的同事发出感叹:“好一波反向输出!”
既然想到固体仿真在医学上的应用,一缕额外的回忆又涌上心头。2016年,我特别想把虚拟人体给产业化,也探索了很多不同的方向。其中比较有意思的,便是与lab师弟,也是好哥们的如今体素科技CEO丁晓伟讨论的整形手术预测。当时我跑了个隆胸动力学预测的demo(包含了对胸部软组织、皮肤、和硅胶假体全方位的模拟),也在洛杉矶聊了一些整形医生,但感觉市场需求度不够大,所以没有继续下去。也不知道元宇宙跨领域越来越火热的今天,这个方向现在怎么样了。
第四章:摩擦摩擦,在光滑的路上,摩擦
前面说到,2012年我便用MPM的思路去尝试处理了破碎仿真里的物体碰撞。但是那个算法只能对付不同碎片之间的碰撞,对自碰撞self collision无可奈何。MPM作为一个用粒子来描述物体的离散格式,毕竟天然最适合如冰雪沙土般像粒子一样的物体。
布料和毛发则是每一个做固体仿真的人都想攻克的东西。科学研究应当尽量以人为本,而布料和毛发跟人的关系真的太大了。处理摩擦碰撞的算法很多,它们做的好的地方都一样优秀,做的不好的地方却五花八门。于是2017年,我重新回到摩擦碰撞这个战场。跟MPM处在105度热恋中的我,选择了一个所有人都没有想过的思路:用MPM塑性去挑战这个课题。
那时我已经学会了Druker-Prager塑性屈服面,并成功用它做出了MPM沙子。沙子的本构模型有两个要素:第一,它支持分开,不支持挤压;第二,它往边上滑的时候,切向力和法向力要满足库伦摩擦定律。仔细回味一番,这两个特性,明明不只是沙子所特有的啊!布料、毛发、橡皮、刚体等等,哪个常见固体的碰撞不是要遵循这两个定律呢?
于是我决定抛弃传统的基于点和三角形,边和边几何相交特性的摩擦碰撞理念(ditto里实现过的那一套),而是采用MPM“连续介质力学”的观点。管他是布料还是毛发,都是一些连续的空间占用而已。在这个观点下,它们跟沙子唯一的区别便是,沙子是三维的“体”,而它们分别是三维空间中二维和一维的曲面。
想到这一点,一切便豁然开朗:如果Drucker-Prager塑性可以让三维的MPM沙子满足摩擦碰撞的性质,那么我只需要推导出二维和一维子空间上所对应的类似的塑性,便可以让MPM布料和毛发满足同样自动摩擦碰撞的性质!
以布料为例,通过对形变梯度的QR分解,我们可以设计一个精巧的弹性能量和塑性屈服面来“管理”布料在法向上摩擦碰撞力所需要满足的应力条件。直观上来讲,在曲面方向,布料仿佛一束束被交织的沙砾,沿着布料的切向望去,满布上都写着两个字“库伦”。
意识到了这一点,处理一维二维曲面的摩擦碰撞便与处理三维沙子的摩擦碰撞别无二致。只需要将这新的本构模型写入曲面上的顶点,MPM便全自动地默默处理了剩下的一切。从布料到毛发,从地毯到毛衣,一切传统的碰撞检测和碰撞处理都被抛弃,一把粒子,一架网格,便能生成一段美妙的动画。这种颠覆式的建模方式,如今我回头看,仍觉得是走出了魔鬼的步伐,是自己学术生涯最满意的MPM论文。
那一年去siggraph 2017宣讲物质点法,抒发的情感只能用已故的李兆基老师的经典台词来形容,“比我的初恋更加诗情画意。”
这篇文章的2D版还在太极语言中被实现了出来(橘子猫:Taichi实现2D Anisotropic Elastoplasticity Cloth),代码十分简洁,妙不可言。后来第二年的SIGGRAPH2018,哥伦比亚大学杀出来一员猛将 Raymond Fei,把这套步法跟APIC结合起来,做了一份令人叹为观止的布料与水相互作用的工作(libwetcloth),一百分的赏心悦目。
参会SIGGRAPH 2017,我还有一个额外的目的:招纳自己的第一个学生。开会时,我在宾夕法尼亚大学的助理教授生涯刚开始不久,孤苦伶仃。一场场灯红酒绿的派对,一间间熙攘喧嚣的酒吧,我在会场外面的夜搜寻着那个可以一起谈笑风生个几年的小伙伴。高级的猎人都会伪装成猎物。
在一个昏暗的角落,我看到一个熟悉的身影在月下独酌,对我目送秋波。那不是一年前张心欣在烤肉店介绍给我的李旻辰吗?我记得他!UBC的一个精壮帅小伙儿,跟张心欣做过一篇流体的文章。我点了两杯火辣的苹果马提尼,摇摇晃晃地走了过去。“还记得我吗?”“记得记得,来,搞一杯!”那一杯,给下一个不醉不归的五年学术夜宴,拉开了序幕。
第五章:少年英雄胡渊鸣
2017年的夏季注定要遇到更多不平凡的人。话分两头,在酒吧初遇李旻辰之前的那一年早些时候,图形学领域广泛流传着这么一个都市传说。有一位策马扬鞭的少年武士,他没有发表过一篇SIGGRAPH论文,但他实现了一百篇;他没有开源过一套代码,但他有一百万行张弓待发;他接手的图形学仿真实现,可以在一夜之间效率提高十倍;他三天没有睡觉,便重现了四年来的所有MPM论文,并且提出了一百种改进的方法。
他究竟是神仙的化身?还是地狱的使者?一时间流言四起,有人甚至说他要建立新的计算机图形学秩序。还在默默想着MPM问题的我更是夜不能寐。这小子,是何方神圣?
他果不出所料地杀上门来了。如想象般翩若惊鸿的胡渊鸣,带着一位比他更加神秘且腼腆的小伙伴,从清华杀到了我UPenn实验室的门口。“我们来跟你一起做MPM。”他的话简短有力。“好,开始吧。”那时的我们,不会寒暄客套,只需要看到一个共同的研究目标便一切尽在不言中。那时他带来的小帮手,叫方火奥,我去google,哦,方燠 yù。现实绝非一帆风顺,我们高速迭代经历了一些失败的科研项目,才最后有了MLS-MPM的发明和后续,简洁而又精彩。
那时,我有一套自己的C++库,远超当年的ditto。我的库叫做“jixie”(机械)。胡渊鸣带来了他的库,叫做“taichi”(太极)。那时太极还是一个C++库。两个库各有千秋,碰撞出许多热烈的火花。胡渊鸣对我助理教授生涯的研究重心,尤其在对榨干计算机性能的追求上,起到了很大的启发性作用。
英雄相惜,终须一别,胡渊鸣要远赴MIT去做别的项目,我在披萨店饯别。“MPM的发展将缓慢下来!”我怅然若失。他笑了笑,告诉我,仍有一个人跟我去打MPM多物理仿真的江山。我目光一瞥,才猛然惊醒,这段时间在刀光剑影里一起谈笑风生的,还有另一位比他更年轻的英雄少年!言辞不多的他,在科研的战场上,虽不像胡渊鸣一样耀眼的艳丽,却散发出一股更加刚猛的炽热。
方燠成为了我第二个学生。如果旻辰是一杯浓厚的酒,底蕴日渐成熟,方燠就是一把嗜血的刀,愈加锋利凶残。他在随后的5年里,把旧论文的实现和新想法的尝试这两件事的速度都做到了像居合斩一般,一刀断骨刀刀落命。
在那段日子里,在方燠、旻辰、和一干猛将的拼搏下,我们一直推进高性能的MPM多物理仿真,直到亿万粒子级别的仿真也变得轻松写意。我们通过跟超算中心的合作,把MPM发展到了能进行Exascale computing的超算机上,每秒算10的18次方个浮点运算。这样看来,对于高分辨率的追求,我们是认真的。
后来,我的实验室汇集了更大一批意气风发的孩子们,屈子吟(ziyin:北京电影学院发了一篇满是数学公式的计算机顶会论文,并开源了其代码) ,仇宇星,王鑫磊,李轩,陈宇诺,曹亚帝,等等,他们围绕着方燠主导架构的C++仿真引擎ziran(自然),在物理模拟的海洋里尽情嬉戏。他们飘逸的学术舞曲还在不断被谱写,有他们在身边,我感觉自己永远抓住了青春,每天都是学术上的“掰饼聚会”:

△To break bread is to affirm trust, confidence, and comfort with an individual or group of people.
在帮助人类打通虚拟世界和现实世界的历史使命上,我们致力于仿真这一个点,用硬核的根基散发千万的枝叶。下面的这些都是我的实验室这些年研究过的方向。这些成果中也充满了极其珍贵的如北京大学朱松纯教授、陈宝权教授、以及浙江大学唐敏教授等前辈传授的经验和给予的帮助。
第六章:与timestep结缘
步者乃一身之根基,运动之枢纽也。——《太极拳十大要论》
在元宇宙的“基础架构”之中,如果建模是内功,渲染是招式,那么物理仿真就是步法或身法。步法与时间和运动紧密绑定在一起,在时间上做微分和积分,从过去预测未来,用未来指引过去。(指引过去,靠的是可微分模拟。)不管是逍遥派的凌波微步,泰森的蝴蝶步法,还是奥拉朱旺的梦幻脚步,它们都反映了一个道理:有一套成熟的步法是一位集大成者立于不败之地的一个可靠的保证。
在动力学物理仿真中,大家最常说的一个词,就是timestep:时间步长,Delta t。正向物理仿真的过程,本质上往往就是微分方程在时间轴上积分的过程,这个过程,又被称为timestepping method;我愿译其为“时间步法”。
现实中的时间是连续的,但仿真中的时间是离散的。对于一段24 FPS的动画来说,每秒钟的理想情况,是让仿真算法从一个过去的时刻往前走24步,每步走1/24秒,生成24个几何形态。除非希望对现实的逼近追求更加极致的准确性,一个通用图形学算法最好具备只需要走24步的能力。如果往前预测1秒需要走48步,或者240步、2400步,那就往往是成倍的效率降低。
可惜的是,直到2015年左右,甚至今日,仍然有无数的图形学仿真算法需要走子步(substeps)。更令人痛苦的是,即使走了子步,它们中的绝大多数仍然不能保证数值的稳定性,俗称“爆了”:
放错图了。爆了的仿真其实长这样:
仿真爆了就意味着得调节参数把程序重跑。我2011年在工业光魔ILM实习,我那时的实习导师告诉我,ILM里在帮复仇者联盟的绿巨人设计肌肉仿真算法,浩克一发力,程序就爆炸,重跑停不下来,delta t 小的不能再小了,机房空调费都要烧个上百万。
为了能够迈出1/24秒或更大的步子,我开始致力于研究基于优化的时间步法。非线性非凸数值优化是一个非常厉害的领域,如今整个神经网络和深度学习都靠它。这个宇宙最基本的物理规律:热力学第二定律(熵增原理)本身也定义了一个优化问题。因此,越来越多的应用数学家开始用优化和变分法的思路去重新思考动力学偏微分方程的数值解。
弹性体模拟的方程便是一个可以重新定义为寻求最小值的优化问题!在此框架之下,时间步长可以迈的任意大,不会扯到蛋。
此间工作很多,图形学里早期工作比较有代表性的,包括刘天添 2014年的巧妙投影动力学“Projective Dynamics: Fusing Constraint Projections for Fast Simulation” 及其2017年的拟牛顿法“Quasi-Newton Methods for Real-time Simulation of Hyperelastic Materials”(2019年(第八届)中国科学技术大学《计算机图形学前沿》暑期课程_哔哩哔哩_bilibili)(冰点蓝:计算机图形学前沿(2019) Towards Real-time Simulation of Deformable Objects),和我2015年参与的比较中规中矩的牛顿法“Optimization Integrator for Large Time Steps”。我的实验室后来则在下面四个地方分点发力:
李旻辰在2019年把拟牛顿法跟domain decomposition结合了起来,打败了一系列竞争对手,得到了一个非常高速度的有限元弹性体解决方案Decomposed Optimization Time Integrator “DOT”(点点有限元法):
王鑫磊则另辟蹊径,考虑多尺度网格multigrid,让MPM也走到了超大的时间步长上面,发明Hierarchical Optimization Time Integrator “HOT”(热辣物质点法),可以高效处理超级“硬”的弹塑性体,帮助工程力学设计的仿真:
方燠则跳出牛顿和拟牛顿的思路,以“快”为目的,把MPM的加速结合上了交替方向乘子法(Alternating Direction Method of Multipliers,ADMM)上。这个方法被称为“Silly Rubber”(愚人橡皮法),可以快速模拟各种MPM适合的材料,比如奶油:
我们最为得意的,也是最新搞出来的,便是李轩、李旻辰和我一起用几支烂笔头推导出来的SIGGRAPH 2022论文Energetically Consistent Inelasticity (ECI)。这个工作在数值计算理论上,我认为有很可观的意义:它首次让塑性力可以迈着同样大的步伐,被真正隐式求解了!也就是说之前的方法,包括上面提到的,都不准,都对塑性力做了一个强相关于 delta t 的其实很不准确的近似。
那算的准有什么好处呢?当然是去跟现实对照了。跟现实连定性的视觉效果都对不上的虚拟物体,步法不够稳健,不能叫数字孪生,永远都只是游戏(没错, 这里说的的正是PhysX/PBD)。我们的坚持,是第一性原理,是我们希望一直尽力朝着真正的数字孪生方向前行的一些固执的原则。
第七章:摩擦碰撞的第三次战役,IPC魔童降世
开始的那些年,从最初level set fracture中的一炮双响,到MPM布料,我一直在跟“摩擦碰撞”这个难题对干。每一场仗都打的很漂亮,但都还是存在很多Limitation。以2017年的MPM布料为例,作为它的缔造者,我比任何人都能更清晰的看到它光芒下令我不堪面对的缺憾。作为一个MPM方法,它在隐式积分条件下性能非常差。
它对粒子和网格的依赖给几何体强加了许多苛刻的要求:比如两者的分辨率需要尽量吻合。同时,它又像一台看似美好的特斯拉自动驾驶汽车,一不小心甩给你一个不大也不小的错误(数值粘性和偶尔的数值穿透),让你在使用时总是心怀忌惮。比如正如下图所示,MPM布料做毛衣虽然厉害,但是仔细看去,还是出现了许多穿透:
穿透会非常严重的影响仿真的精度和可信度。它不只是模型视觉上的错误,随之而来的弹性力和摩擦力也会因穿透而变得离谱和虚幻。因此,长久以来,至少在布料这一个小方向上,我并没有能够把MPM从特效和游戏的应用中打出去。换而言之,因我坚信元宇宙和游戏的最重要区别是对“准”的把握上(这也是我不认为NVIDIA的omniverse拿着一个基于不物理方法推导出来的PhysX引擎可以做成真正元宇宙物理引擎的根本原因),MPM在布料这个方向上要走的路还很长,还需要后来者的努力。
时钟拨到2020年前夕,没有征兆又似蛰伏许久的一件事情发生了。之前我把旻辰比作美酒,他便真的是这样一个学生,在陈酿的千锤百炼中一不小心就饱满丰厚,醇香持久。没几年,他便从一个学生潇潇洒洒地蜕变为一个成熟的合作伙伴。
那晚,我郑重的告诉旻辰,“你刚完成的这个叫做IPC的项目,把一个困扰了计算机图形学和工程力学无数研究者几十年的一个领域给终结掉了,完美本无法触及,但IPC是我入行以来见过的,最接近完美的仿真技术。”在这一年后,旻辰以IPC斩获SIGGRAPH年度最佳博士论文奖,毫无悬念。
IPC的全称是Incremental Potential Contact,中文作增量势能接触,很拗口,还是就叫IPC吧。它的算法冗长而又毫不晦涩,刚猛而又不失优雅。在数值优化的框架下,IPC把所有基于mesh的物理仿真中“不许穿透”这个令学术界和产业界都为之痴迷的难题,从仿真问题的数学形态上就直接通过一个灵巧的定义给彻底毙掉了,其后的算法自然是如出入无人之境。“从此穿模是路人。”
技术上,IPC提出了一个崭新而又巧妙的关于“碰撞”的数学描述方法:所谓碰撞,便是在动力学过程的最小作用量原理下,要求任何非邻接几何表面之间的欧氏距离在连续的时间轴上恒大于零。它正是又一个timestepping的时间步法!如此一来,我们得到了一个可以用数学完美描述的约束优化问题。再配以些许精巧而不诡野的算法设计,最终的IPC技术在数学、算法和实现上都令人信服。毫不夸张的说,IPC是数值仿真自发明以来,唯一的把精确碰撞和摩擦这两个要求完美解决掉的办法。它唯一的缺点是计算效率不够快;被我们后来攻克,按下不表。
IPC及其2021年后续工作赋能了无数之前计算机仿真界根本做不了的事情,以绝对的稳定性、精确性、和数值收敛性涵盖了三维柔性体(“百万四面体的毛球”和“是绳子就坚持一百秒”):


二维布料(轻松处理打结,和任意多层布料上身,这里只展示了四层,毕竟我们的建模制版技能点加的比较少):

二维薄壳(跟真实的一叠扑克牌的厚度完全吻合,没有任何别的方法可以做到)(这是不是可以拿去开元宇宙赌场?):
以及首次有“不穿透保证”与“精准摩擦力”两个性质的的一维细杆(面条、毛发):

旻辰向来沉稳低调,他宣传IPC的文章(李旻辰:IPC: SIGGRAPH 2020开源有限元碰撞独家处理方案)也跟他的人一样靠谱实在。2020年1月,我在IPC的第一篇论文里,写下过这么一段总结(中文意译略有改写):
IPC技术适用于所有基于网格的固体模拟。无论是自碰撞、外碰撞、甚至是来自于低维曲面的碰撞,IPC都是一个绝顶灵活、有效、和无条件保证成功的解决方案。IPC对图形学和工程力学基于或不基于有限元的全部应用都提供了有史以来第一个几何不穿透,体积不反转的可证明的直接保证。从此以后,跑固体仿真只需要输入真实世界可以测量的物理参数和几何参数,而再不需要去调节所谓的数值参数。在此之上,IPC承诺必定能够对任意复杂的状态给出求解,并且这个解就是这个世界上现存所有算法能给出的,最接近真实世界摩擦碰撞结果的解。
几年过去了,这个总结被图形学、机械工程、以及机器人领域的同行不断的引述和验证。作为一个学者,我从未如此夸过一个工作,毕竟有吹牛皮之嫌。但是IPC不一样,我不担心,因为这个牛皮是钢铁铸成,永远也吹不破。
IPC这么完美,还有什么可以改善的呢?正如上文所说,它的计算效率存在一定的问题。在我们一筹莫展之际,一位老友突然与我们取得了联系。此人名作阴阳(Yin Yang),继胡渊鸣之后成为第二个让我瞧见八卦图头像便能开怀之人。克莱姆森大学的杨垠教授(现在迁去了犹他大学)姗姗来迟,他是降维仿真和GPU加速仿真的代表人物。我们一拍即合,开始建立深厚的革命友谊。自那天起,杨垠、旻辰和我开始了围绕IPC技术的一系列深度合作项目。在我们的思维火花碰撞之下,浩如烟海的脑洞和研发项目扑面而来。以2022年为例,我们便让IPC生态系统在刚体仿真和实时仿真两个方向取得了不亚于原始IPC的崭新成果。
第一个成果,是我们在刚体仿真上取得的重大成就。刚体与柔性体自古以来便被分开处理,求解它们的方法不能说是关系不大,只能说是几乎毫无关系。在IPC的加持下,我们提出了崭新的“Affine Body Dynamics (ABD)” 仿射体动力学,在淘汰传统刚体模拟的路上直接飙到终点,让刚体重新回归成它们在真实世界中的样子:即使最硬的物体,也会微小的形变,硬度是振金还是木头,该是多少就是多少,不需要被假设成绝对刚体。在ABD技术的加持下,我们在拥有所有IPC优点的同时,达到了媲美现有刚体引擎的速度和全方位碾压的精度。高速而又精准的机械体仿真首次成为可能。
真实碰撞驱动的齿轮:

及其受力分析:

带传动结构的小车(含简易气缸):
及其传动引擎的简易气缸运动的可视化(活塞运动带动旋转):
铁链弹性波的传播:
比较传统的场景当然也不在话下:
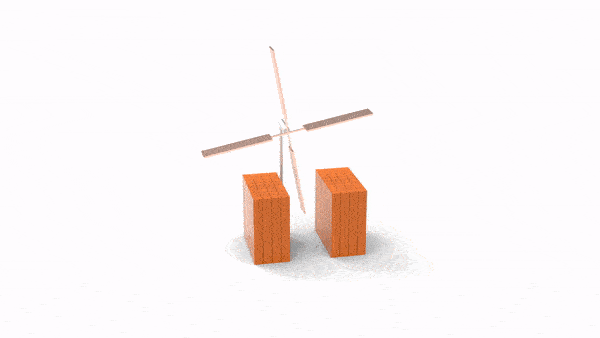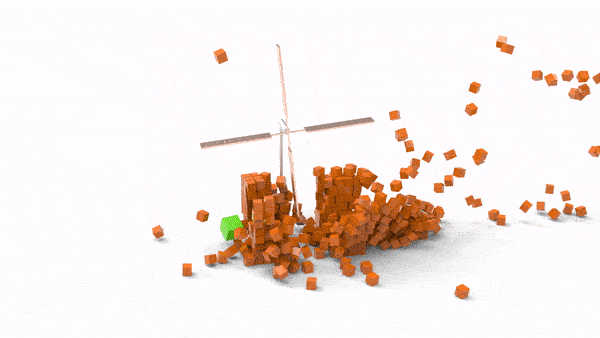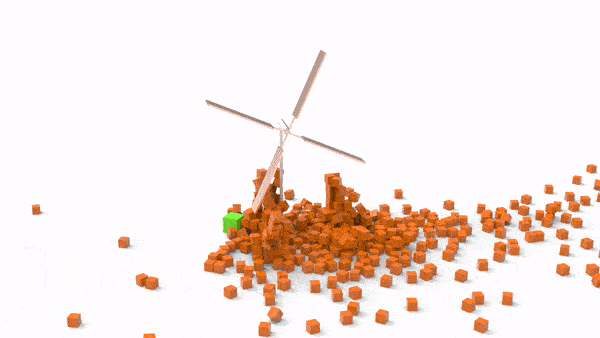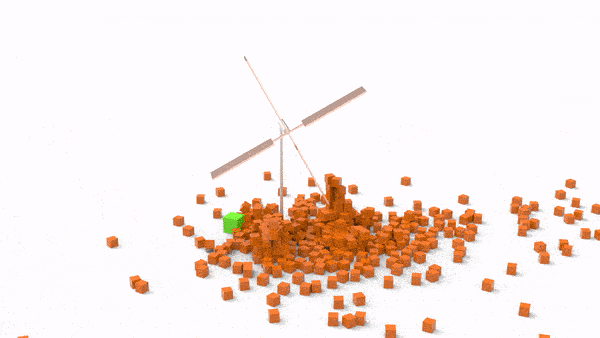
值得一提的是,ABD在机器人抓取的任务上,已经被机器人领域的学界和工业界同行验证,其成功率和对接触力/摩擦力的准确性上,已经远远超过了PBD、Bullet、Mujoco等一众现有刚体引擎;强化学习在我们的solver上,轻松训练出了真正可以转化到物理世界的控制算法,误差之小,模拟过程之惬意,非机器人业内人士不可言喻:

英伟达Omniverse也宣传了很多工业机器人的场景,它的技术仍然基于PhysX(PBD),那套简单易学但毫无真实物理原则的手段。剩下的一切,还何须多言呢?也许在有些人心中,元宇宙只需要以假乱真,”看上去差不多就行了。”那么,就等时间给出“自然”选择的答案。
我从方法论上表述我自己的观点。我认为,像PBD一类的技术,以快为出发点,在当年的低下算力和就是面向游戏的两个前提下,无可厚非。但是由于对数学和物理原理的修改与简化,使其在元宇宙的未来想要从快到准,路途难如蜀道。
与它们截然不同的是,IPC直接先把“准”这一步做到了几乎完美,那么在这个前提下,再做快有多难呢?在算数、算法、算力的三重加持下,IPC加速之路顺畅无阻。举例而言,我们2022年的第二个成果,便轻松地实现了多层布料的实时交互仿真,并且,没有牺牲任何IPC在碰撞上所承诺的美好保证:
第八章:下一个“Timestep”
十二年,我从C++都不会写的等离子体物理专业的学生,到拿到CS PhD,去常青藤做CS教授,再到UCLA应用数学拿tenure,回想一下,这其中竟没有一年被浪费,纯粹跟着喜爱的研究走,顺其自然。记得网上常有人讨论@计算机图形学的交叉学科本质。我想我本人应该就是一个不错的活标本吧。十二年的职业道路上,我也是无比幸运(毕竟射手座),遇到了太多牛逼的师长、同学、挚友、和学生,每个人都让我学到了很多。
那下一个十二年,我应该主要做些什么呢?思考了许久,不为立志,但求有一个计划。我想, “closing the gap between virtual reality and physical reality”,这个目标绝没有变,围绕物理仿真这一指引运动规律的轴心的原则也依旧在我心上打着思想钢印。在此之外,我与携有同样想法的三个人(李旻辰,方燠,杨垠Yin Yang)一起成立了Timestep,致力于稳健、精准、高效、普适的物理仿真“步法”及它们在不同产业中的应用,并在国内以及世界多地积极打造和布局一个可持续发展的体系。万水千山不停步,希望在下一个十二年,我们跟更多同道中人一起,通过有趣和有用的技术和想法把虚拟世界和现实世界真正打通。
《从转系生到终身教授:十二年图形学物理模拟的自我回顾》:
https://zhuanlan.zhihu.com/p/560415998
— 完 —
「人工智能」、「智能汽车」微信社群邀你加入!
欢迎关注人工智能、智能汽车的小伙伴们加入我们,与AI从业者交流、切磋,不错过最新行业发展&技术进展。
PS. 加好友请务必备注您的姓名-公司-职位哦 ~

点这里👇关注我,记得标星哦~
一键三连「分享」、「点赞」和「在看」
科技前沿进展日日相见~