时空预测概述及多任务时空网络的交通预测

   

预览摘要：

时空网络中的流量预测(如车辆、人群和自行车的流量)由一个节点的输入输出流量和不同节点之间的过渡组成，在交通系统中起着重要的作用。然而，这是一个非常具有挑战性的问题，受到多种复杂因素的影响，如不同地点之间的空间相关性，不同时间间隔之间的时间相关性，以及外部因素(如事件和天气)。此外，节点处的流(称为节点流)和节点之间的过渡(边流)相互影响。为了解决这些问题，作者提出了一种多任务深度学习框架，该框架能够同时预测时空网络中的节点流和边流。基于完全卷积网络，设计了两个复杂的模型，分别用于预测节点流和边流。这两个模型通过耦合其中间层的潜在表示而连接在一起，并一起训练。外部因素也通过门控融合机制集成到框架中。在边流预测模型中，使用了一个嵌入组件来处理节点之间的稀疏过渡。基于北京和纽约的出租车数据对方法进行了评估。实验结果表明，该方法在ConvLSTM、CNN、马尔可夫随机场等11条基线上都具有较好的优势。

文章亮点总结：

这篇文章除了从数据中挖掘节点流之间的关系来预测交通流量外，还挖掘了边流的信息，即进行了流向预测并提出了一个基于边流和节点流之间关系的新损失函数。

相关热点文章推荐：

IJCAI2019 长时段交通预测解决方案

强化学习在智能交通灯中的应用

交通级联模式挖掘

[AAAI2020]*图注意力机制网路用于交通预测

最近火爆的人工智能2.0--图神经网络，究竟什么来路？ 

更多相关专业文章，欢迎关注公众号【图与交通】！

时空预测概述

根据应用场景，将其分为了三类：1、短期交通流预测。2、城市路网的中短期和长期交通流预测，中短期是5-30分钟，长期是超过30分钟。这里的交通流预测可以是交通速度、交通流量或者交通密度。3、区域交通流预测，一般在这个应用场景中，实验数据都被预处理为栅格数据。有些论文还会进行流入流出预测。

• 短期交通流预测

• 《Short-term traffic flow prediction with Conv-LSTM》--2017WCSP

             

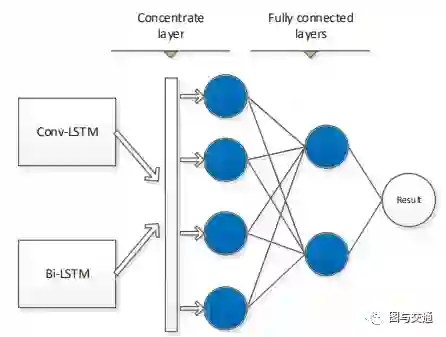
本文介绍了利用ConvLSTM模块对相邻区域的短时交通流数据进行处理，提取时空特征以及利用双向LSTM对预测点历史交通数据进行处理，提取交通流数据的周期特征的方法。提出了一种无需数据预处理和数据特征提取的端到端深度学习短时交通流预测体系结构。最后，集中时空特征和周期特征对交通流进行预测。这也是这方面问题的baseline之一。

• 《Diffusion Convolutional Recurrent Neural Network: Data-Driven Traffic Forecasting》--2018ICLR

             

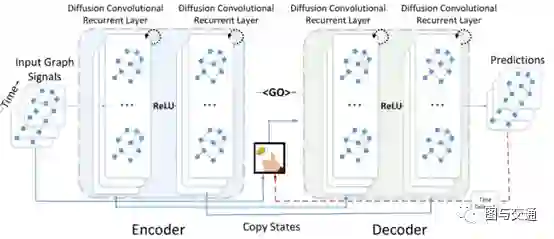
提出了基于扩散卷积循环神经网络(DCRNN)的交通流预测，它将交通流建模为有向图上的扩散过程，DCRNN使用图上的双向随机游走捕获空间依赖性，以及使用具有调度采样的编码器 - 解码器架构的时间依赖性

• 《T-LSTM: A Long Short-Term Memory Neural Network Enhanced by Temporal Information for Traffic Flow Prediction》--2019IEEE ACCESS

             

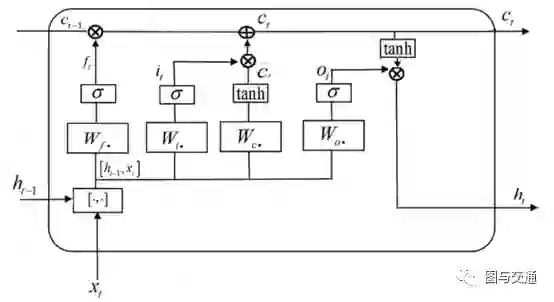
提出了一种时间信息增强LSTM（T-LSTM）来预测单个路段的交通流量。考虑到每天同一时间的交通流量的相似特性，该模型可以通过捕获交通流量与时间信息之间的内在关联性来提高预测准确性。

• 《City-Wide Traffic Flow Forecasting Using a Deep Convolutional Neural Network》--2020SENSORS

             

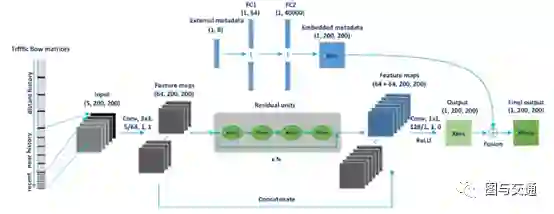
提出了一种基于深度学习的多分枝预测模型来预测城市的短期交通流量。在这里它引入了外部因素这一概念，例如天气、突发交通事故、节假日等都会影响交通流量。该模型利用时空交通流矩阵和外部因素作为输入，推断并输出整个路网未来的短期交通状态(流量)。为了模拟当前路段和相邻路段之间的交通流的空间相关性，采用多层全卷积框架进行互相关计算，并从局部到全局尺度提取分层空间依赖关系。同时，通过从时间轴上的近、中、远三个时间段构造交通流矩阵组成的高维张量，从历史观测中提取交通流的时间贴近性和周期性。同时考虑外部因素，用完全连接的神经网络进行训练，然后与TFFNet也就是这个模型的框架的主成分的输出进行融合。多分支模型被自动训练以拟合隐藏在交通流矩阵中的复杂模式，直到通过反向传播方法达到预定义的收敛标准。

在短期交通流量预测方面，以前的论文多应用RNN及LSTM等的变体进行研究，这种研究方法主要考虑了交通数据的时间特征，就是2020年的这篇文章也是将时间特征和空间特征进行分开研究的，但是在交通数据中其实不可分的时空特征能包含更多有用的信息。

• 中短期和长期交通流预测

• 《Spatio-Temporal Graph Convolutional Networks: A Deep Learning Framework for Traffic Forecasting》--2018IJCAI

             

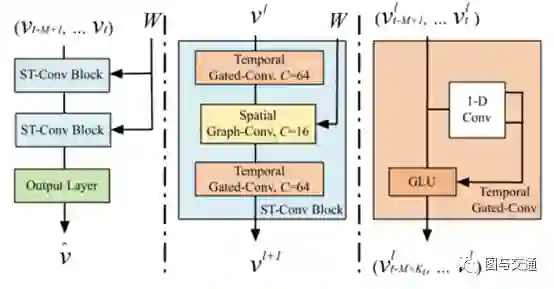
提出了一种新的深度学习结构，时空图卷积网络，由多个时空卷积块组成，时空卷积块由图卷积层和卷积序列学习层组合而成,对时空依赖关系进行建模。

• 《T-GCN: A Temporal Graph Convolutional Network for Traffic Prediction》--2019ITSS

             

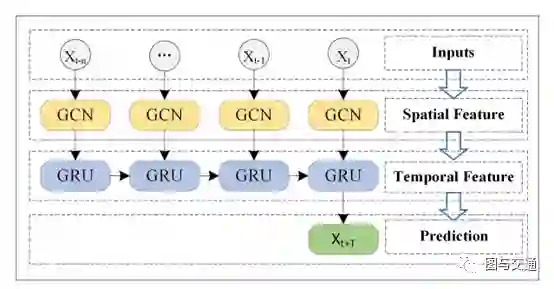
该模型结合了图卷积网络(GCN)和门控递归单元(GRU)。GCN用于学习复杂的拓扑结构来捕获空间依赖关系，GRU用于学习交通数据的动态变化来捕获时间依赖关系。

• 《Attention Based Spatial-Temporal Graph Convolutional Networks for Traffic Flow Forecasting》--2019AAAI

             

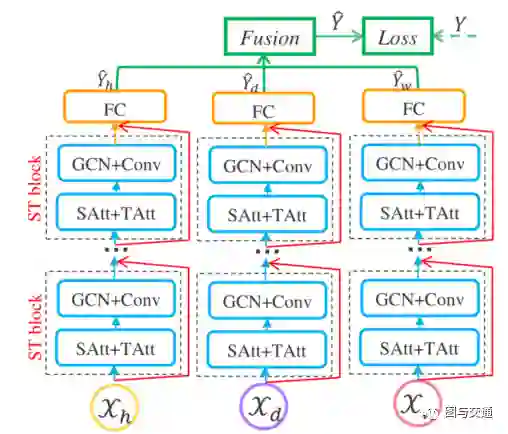
    介绍了基于注意力机制的时空图卷积网络(ASTGCN)来做交通流预测。ASTGCN主要由三个独立部分组成，分别对交通流的三个时间特性进行建模，即邻近、每日和每周的依赖关系。其中每个独立部分又包含两部分:1)时空注意力机制，有效地捕捉交通数据中的动态时空关联; 2)时空卷积，即同时使用图卷积来捕捉空间模式和常用的标准卷积来描述时间特征。对三个分量的输出进行加权融合，生成最终预测结果。

• 《Multi-Range Attentive Bicomponent Graph Convolutional Network for Traffic Forecasting》--2020AAAI

             

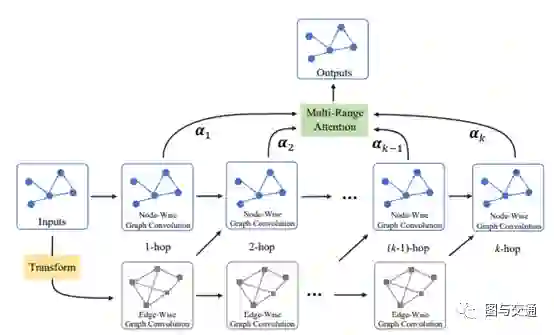
   在前一年研究的基础上提出了多范围注意力双组分GCN（MRA-BGCN），这是一种用于交通预测的新型深度学习模型。首先根据路网距离构建节点图，并根据各种边沿交互模式构建边图。然后，使用双分量图卷积实现节点和边的交互。引入了多范围注意力机制来汇总不同邻域范围内的信息，并自动了解不同范围的重要性。最新研究主要集中在通过在整个固定加权图中利用图卷积网络（GCN）来对空间依赖性进行建模。这篇论文主要考虑到边，即成对节点之间的相关性，要复杂得多并且彼此相互作用。所以在这方面做了一些创新。

• 区域交通流预测

• 《Deep Spatio-Temporal Residual Networks for Citywide Crowd Flows Prediction》--2017AAAI

             

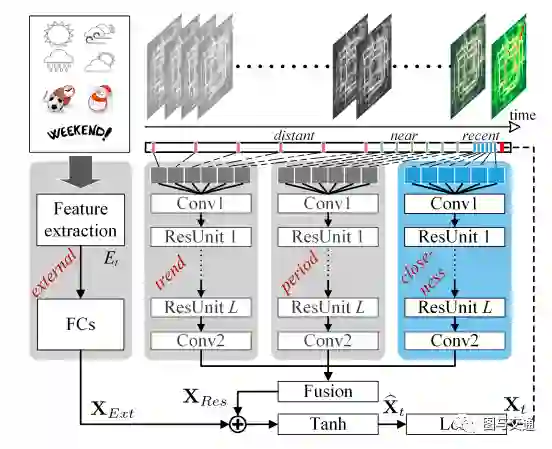
   作者用残差神经网络框架对拥堵流的时间临近性、周期和趋势特性建模（closeness, period, trend）。针对每个属性，设计了一个残差卷积单元的分支，每个残差卷积单元对拥堵流的空间特性进行建模，ST-ResNet动态整合三个残差神经网络分支的输出，为不同的分支和区域分配不同的权重。将整合结果进一步结合外部因素（external），如天气和一周中的哪一天，来预测每个地区最终流量.

• 《Revisiting Spatial-Temporal Similarity: A Deep Learning Framework for Traffic Prediction》--2019AAAI

             

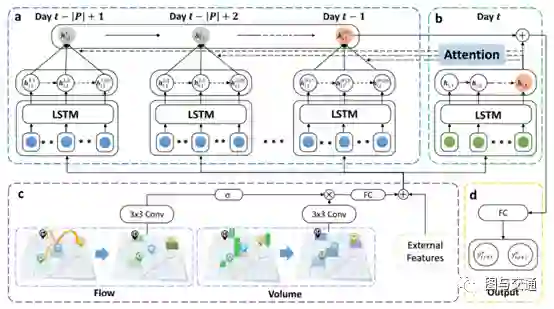
   这篇文章是为了解决两个问题，1、区域间的空间依赖是动态的；2、时间依赖虽说有天和周的模式，但因为有动态时间平移，它不是严格周期的。本文提出基于时空神经网络的，使用局部 CNN 和 LSTM 分别处理时空信息。一个门控局部 CNN 使用区域间的动态相似性对空间依赖建模，一个周期平移的注意力机制用来学习长期周期依赖的模型。总的来说，通过注意力机制对长期周期信息和时间平移建模的深度学习框架。

• 《Deep Spatial–Temporal 3D Convolutional Neural Networks for Traffic Data Forecasting》--2019ITSS

             

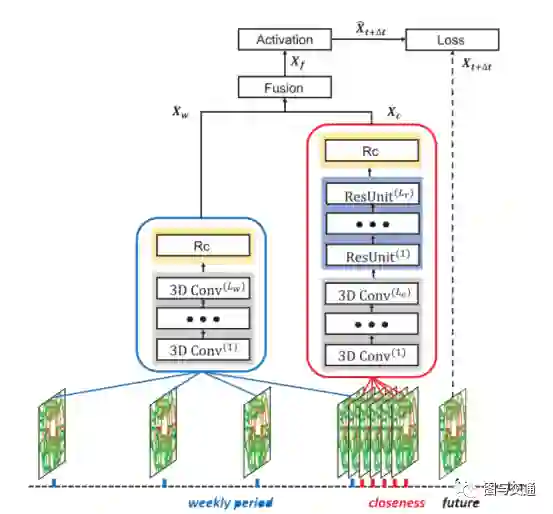
   ST-3DNet引入了3D卷积来自动捕获交通数据在空间和时间维度上的相关性。提出了一种新的重新校准(RC)块来显式量化空间相关性贡献的差异。考虑到交通数据的两种时间特性，即局部模式和长期模式，ST-3DNet采用由三维卷积和RC块组成的两个分量分别对这两种模式进行建模，然后将它们加权聚合在一起进行最终预测。这篇文章主要解决的问题是交通数据是一种典型的时空数据，在空间和时间上同时表现出相关性和异构性。已有的工作大多只能捕捉交通数据的部分属性，甚至假设相关性对交通预测的影响是全局不变的，导致建模不充分，预测性能不理想。

• 《Flow Prediction in Spatio-Temporal Networks Based on Multitask Deep Learning》--2020TKDE

             

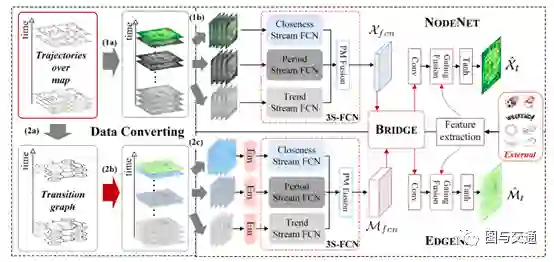
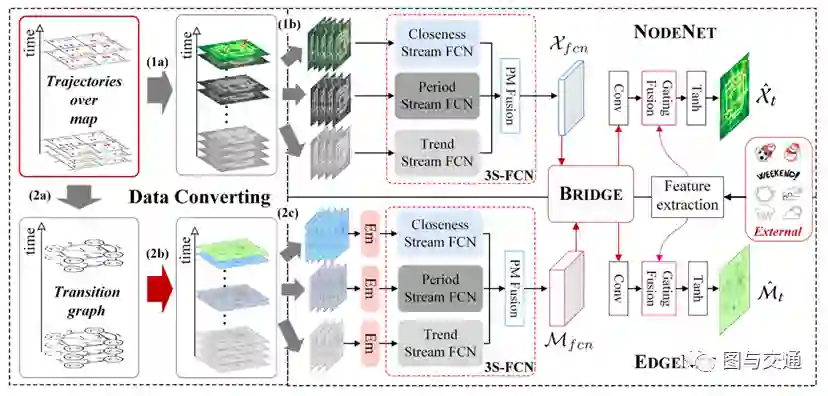
   本文设计了一个基于时空多任务学习框架(MDL)来对区域交通进行流量预测与流向预测。一个深度神经网络来预测顶点流量（命名为 NODENET），另一个深度神经网络预测边流量（命名为 EDGENET）。通过将他们的隐藏状态拼接来连接这两个深度神经网络，并一同训练。此外，这两类流量的相关性通过损失函数中的正则项来建模。基于深度学习的模型可以处理复杂性和尺度等问题，同时多任务框架增强了每类流量的预测性能。下面将具体介绍这篇论文。

2. Node Flow and Edge Flow

• node flow: the in—and out-flows at a node

outflow metrices:              

inflow metrices:              

             表示节点(x,y)在区域点r中，              表示此时的时间戳在时间区间t内，(s,e)表示起终点对，P为所有的起终点对。其中起点和终点由              表示。

             

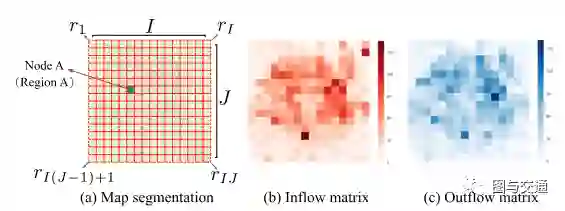
• edge flow: the transitions between nodes 

              

             

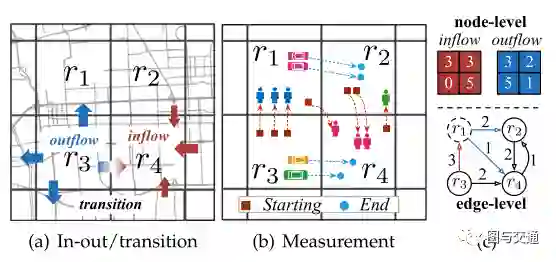
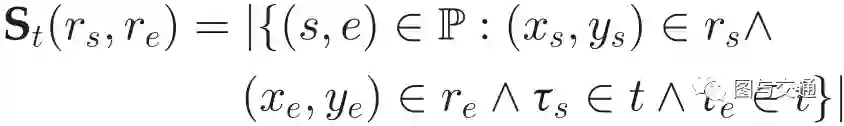
St是区间t内的转移矩阵，即从节点Rs到 Re的转移。

在交通系统中，这两种类型的流量可以通过：1、附近道路行驶的小汽车数量；2、乘坐地铁/公共汽车的人数；3、行人数量；或者，4、如果有数据，全部加在一起来衡量。

图b给出了一个插图。以节点R1为例，分别根据手机信号和车辆的GPS轨迹计算流入流量为3，流出流量为3。我们可以看到从r3到r1的过渡是3，从r1到r2和r4的过度分别是2和1。在这里我们可以看到两种类型的流量，一种是节点流，一种是边流，就如图c所示。所有边上的过渡被视为有向图。

 

3. 挑战

由于以下几个方面的原因，同时预测ST网络的所有节点上的输入/输出流量和边缘上的过渡是非常具有挑战性的：

• 规模和复杂性：位置的流入/流出取决于地理空间中的近邻和远邻，因为人们可以在任何位置之间过境，特别是当一些事件发生在城市中时。给定一个具有大量(N)个位置的大城市，有N的2次方个转换的可能性，尽管这些转换可能不会在某个时间间隔同时发生。但是，要预测位置流，无论是输入/输出流还是过渡流，我们都需要考虑一个城市的位置和其他地方之间的依赖关系。此外，预测还与过去时间间隔的流量有关。并且，我们不能单独和分别预测每个地点的流量，因为城市中的地点是相互联系、相互关联和相互影响的。这种复杂性和规模性对概率图模型等传统的机器学习模型提出了巨大的挑战。

• 对多重相关性和外部因素进行建模：在处理这样的预测问题时，需要对三种类型的相关性进行建模。第一种是不同位置的流量之间的空间相关性，包括近位置之间的相关性和远位置之间的相关性。第二种是不同时间间隔的交通流之间的时间相关性，包括时间贴近性、周期性和趋势性。第三，进出流与过渡流高度相关，相互促进。流入某个位置的过渡总和是该位置的流入。同样，准确预测某个位置的总流出流量可以帮助更准确地预测从该位置到其他地方的过渡流量，反之亦然。此外，这些流量还受到事件、天气和事故等外部因素的影响。

• 动态性和稀疏性：由于N的2次方的可能性，位置之间的转换流随时间的变化比输入/输出流的变化要大得多。在下一个时间间隔真正发生的转变可能是N的2次方种可能性中非常小的一部分(即非常稀疏)。在如此高维的空间中预测如此稀疏的转变是一项非常具有挑战性的任务。

  
  

4. 框架

             

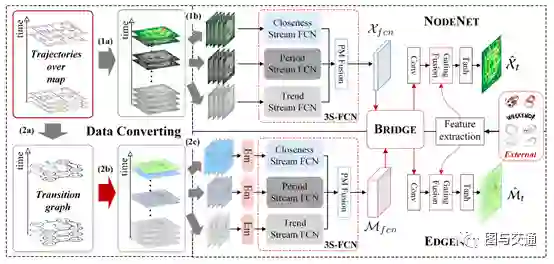
框架由三个组件组成，分别用于数据转换、节点流建模和边流建模。如图的左侧所示，首先将沿时间的地图上的轨迹(或行程)数据转换成两种类型的流：节点流是按时间排序的张量序列。边流作为图(转移矩阵)的时序序列，它被进一步转换成张量序列。

2. Data Converting

为了将深度神经网络应用于时变图，作者建议首先将时间t处的每个图转换为张量。给定时间t的一个有向图              ，首先展开它，然后计算有向权矩阵(例如，转移矩阵)，最后得到张量。以下给出具体说明。

             

 

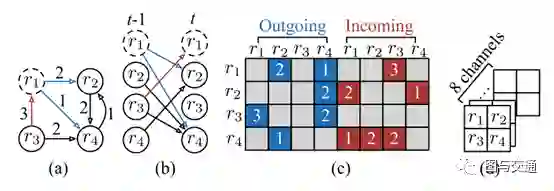
(A)给定一个在时间t由4个结点和6条边组成的图。(B)首先展开它，这是一个有向图。(C)对于每个节点，都有传入和传出转换，由向量表示(维数为8)。以节点r1为例，其传出转移向量和传入转移向量分别为[0;2;0;1]和[0;0;3;0]，它们进一步连接成一个向量[0;2;0;1;0;0;3;0]，包含传出和传入信息。(D)最后，将矩阵重塑为张量，其中每个节点根据原始地图分割具有固定的空间位置，保护了空间相关性。

然后，这两种类型的类似视频的数据分别被送到NODENET和EDGENET。以EDGENET为例，选取了三种不同类型的片段，并将其送入3S-FCN，该模型可以对时间相关性进行建模，包括贴近度、周期和趋势。其中，每个streamFCN都可以通过多次卷积捕获空间近距离相关性。NODENET和EDGENET中间层的潜在表示由BRIDGE组件耦合，并一起训练。使用一个嵌入层(称为Em)来处理过渡稀疏性问题。门控融合组件用于整合外部因素。此外，节点流和边流之间的相关性由^Xt和^Mt之间的正则化来建模.

2. EDGENET

根据上述转换方法，每个时间间隔的转换图可以转换为张量，对于每个节点Rij，它具有高达2N的转换可能性，包括N个输入和N个输出。然而，对于特定的时间间隔，节点之间的转换可能非常稀疏。因此，作者受nlp的嵌入方法的启发提出采用空间嵌入方法来解决这种稀疏和高维问题。具体而言，空间嵌入倾向于学习将节点Rij的2N维向量映射到k维空间的函数:

             

其中W和B分别是可学习参数矩阵和向量，所有节点共享这些参数，M为位于方阵(i,j)的向量。

流量，就像城市中的人群交通一样，总是受到时空依赖性的影响。为了捕捉不同的时间依赖关系(封闭度、周期和趋势)提出了一种沿时间方向选择不同关键帧的深度时空残差网络。受此启发，作者在此选择最近关键帧、近关键帧和远关键帧来预测时间间隔t，分别表示如下所示：

             

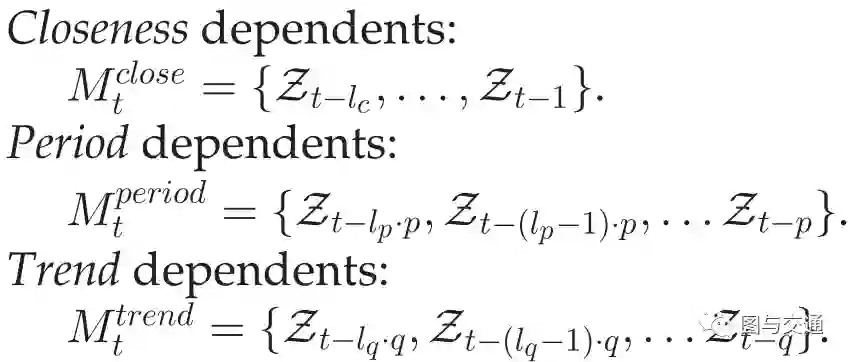
其中p和q分别是周期跨度和趋势跨度。Lc、Lp和Lq是序列的这三个部分的长度。

因为这里的输出(即，下一时间间隔的预测)具有与输入相同的分辨率。这样的任务非常类似于图像分割问题，所以它可以由完全卷积网络(FCN)来处理。受此启发，作者提出了一个3SFCN来捕获时间封闭性、周期和趋势依赖关系。其中，每个流都是一个FCN，由许多卷积组成。根据卷积的性质，一个卷积层可以捕获空间近相关性。随着卷积层数目的增加，FCN可以捕获越来越远的依赖关系，甚至城市范围的空间依赖关系。然而，这样的深层卷积网络变得非常难以训练。因此，使用剩余关系来帮助培训。与残差网络中使用的残差块类似，这里使用由批归一化(BN)、校正线性单元(RELU)和卷积(Conv)组成的块。

             

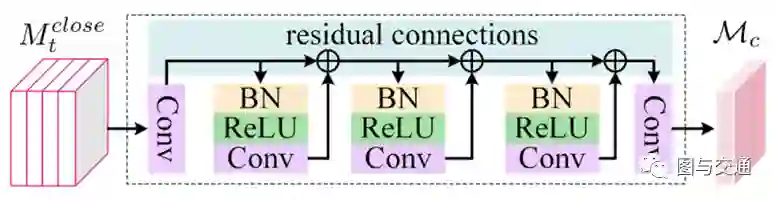
设接近流、周期流和趋势流FCN的输出分别为Mc，Mp，Mq。不同的节点可能具有不同的贴近度、周期和趋势属性。为了解决这个问题，作者建议使用基于参数矩阵的融合(PM融合)来合并它们。

             

Wc，Wp，Wq分别是调整受时间贴近度、周期和趋势影响程度的可学习参数

3. NODENET

与EDGENET类似，NODENET也是一个3S-FCN，选择最近关键帧、最近关键帧和远离关键帧作为距离、周期和趋势依赖项。不同的是，NODENET没有嵌入层，因为输入的通道数只有2个。这三组不同的从属对象被馈入三个不同的流FCN，其输出也由PM融合组件进一步合并。然后，我们可以得到3S-FCN的输出。

4. 融合机制

1. Concat Fusion

   考虑到节点流和边流是相关的，所以从NODENET和EDGENET中学习到的表示应该连接起来。为了连接NODENET和EDGENET，假设NODENET和EDGENET的两个潜在表示分别为Xfcn和Mfcn。考虑到直接融合方法的前提是两个任务的表示必须具有相同的形状，即Xfcn和Mfcn在信道维度上具有相同的大小。为了能从束缚中解脱出来。提出了一种称为CONCAT的融合方法，两个潜在表示映射Xfcn和Mfcn在同一空间节点Rij跨通道c的拼接如下：

             

             

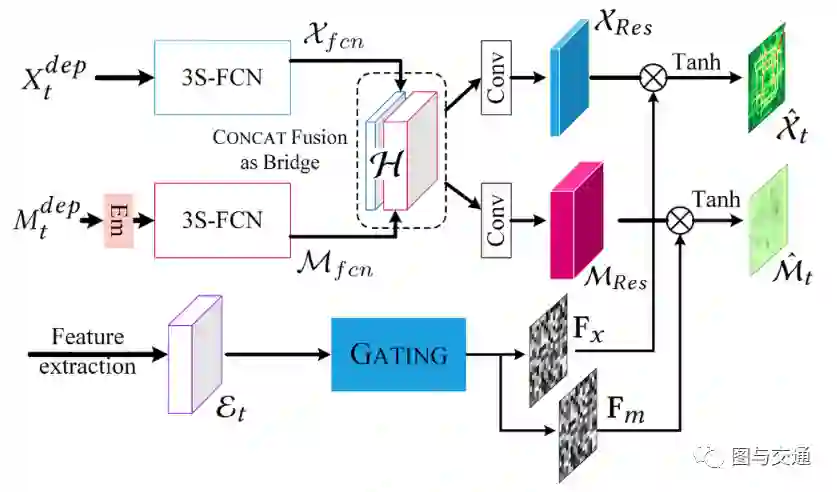
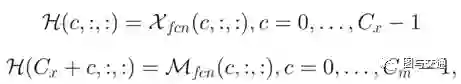
   其中Cx和Cm分别是Xfcn和Mfcn的通道数， Concat融合实际上可以通过相互加强更好地整合节点和边流的两个层次。在CONCAT融合后，分别在NODENET和EDGENET中添加卷积层。使用卷积将组合的潜在特征映射图H映射到不同大小的通道输出。

2. Gating Fusion

   外部因素，如事件和天气，可以影响ST网络不同部分的流量。例如，一场事故可能会堵塞某一地区的交通，一场暴雨可能会减少全球范围内的交通。这种外部因素就像开关一样，如果发生了，流量会发生很大的变化。基于这一认识，在这里发展了一种基于门控机制的融合，如图所示。在时间t，人们可以获得ST-网络中相应的外部特征，表示为ET。

             

             

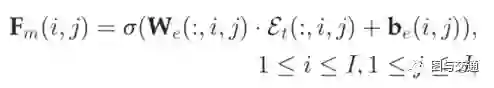
   Fm是对应节点Rij的STnetwork的gating值，w和b是可学习的参数。然后使用基于门机制的融合。其中tanh是确保输出值在-1和1之间的双曲正切。同样的，在NODENET的最终预测中，FX是gating的另一个输出。对节点流和边缘流使用不同的gating值(即，F)的一个原因是，外部因素可以不同地影响不同位置的输入/输出流和转换。

5. LOSSES

                            

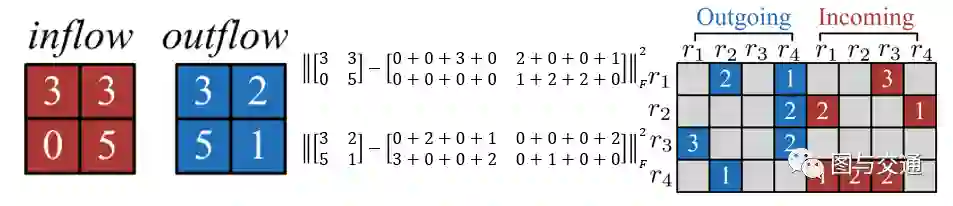
总的来说损失函数包含三个部分，其中Jedge和Jnode好理解，分别表示两个网络各自的损失。而Jmdl则表示二者结合起来的损失。Qc是mt所有非零项的指示矩阵。Pt是xt中所有非零项的指示矩阵

从本质上说左右两边的表示是等价的，因此二者之间的损失应该为0。因此图中红色部分也就对应公式中的红色部分；蓝色对应蓝色公式。

 

5. 实验

1. 数据集

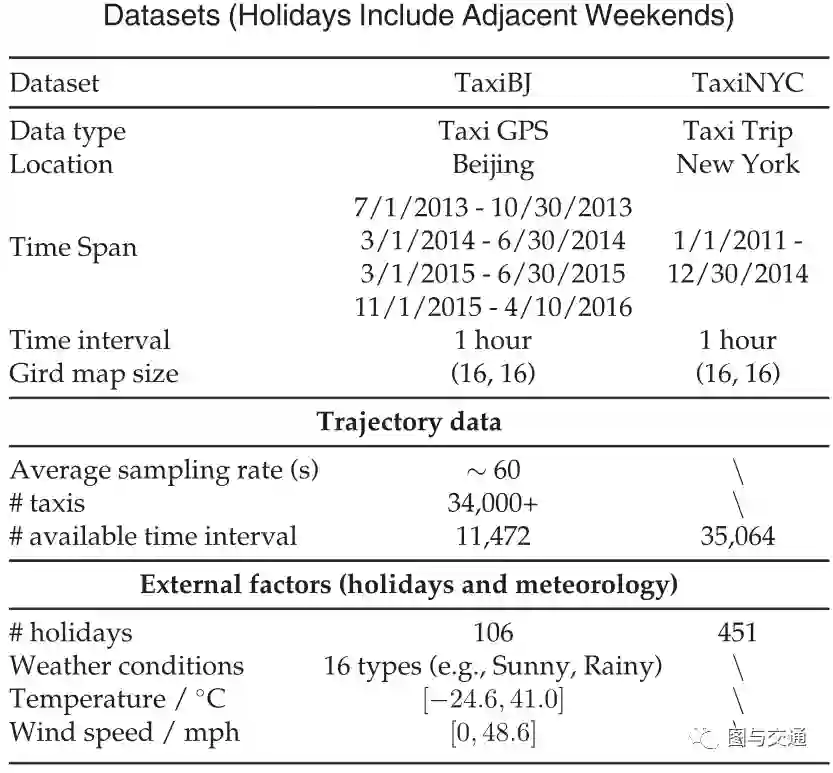
• TaxiBJ：轨迹数据是指2013年7月1日-2013年10月30日、2014年3月1日-2014年6月30日、2015年3月1日-2015年6月30日、2015年11月1日-2016年4月10日四个时间段的北京市出租车GPS数据和气象数据。作者选择过去四周的数据作为测试集，之前的所有数据作为训练集。

• TaxiNYC：出租车出行记录取自2011年至2014年的纽约市。出行数据包括：接送日期/时间、接送地点。在这些数据中，最后四周被选为测试集，其余被选为训练集

              

2. baselines

             

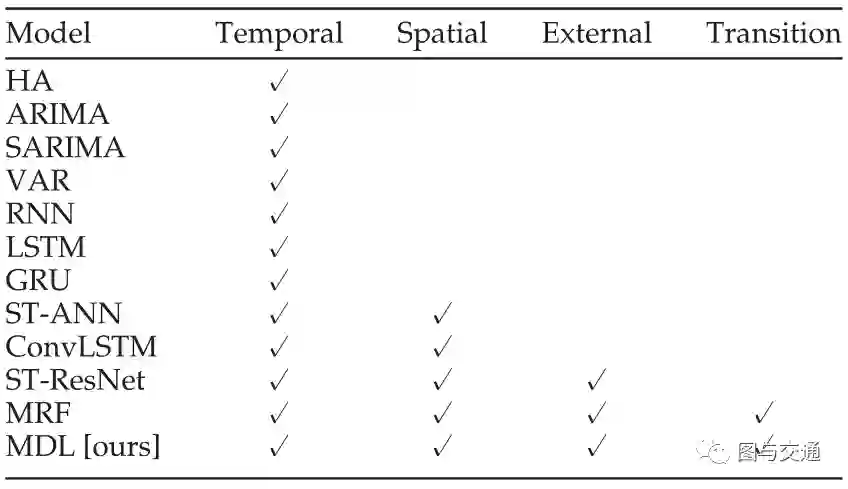
Baselines一共有以上11种，只考虑时间信息的7种，加上考虑空间信息的两种，考虑外部信息的ST-Resnet和考虑了过渡信息的MRF。前面的经典统计方法和rnn及其变体不用赘述，下面来说一下剩下的baselines.

ST-ANN：时空人工神经网络，以空间(邻近8个区域)和时间(前8个时间间隔)值作为输入特征。

ConvLSTM：卷积LSTM，一个使用雷达回波数据集(图像序列)进行降水短时预报的最新模型。本文中使用的人群流数据可以看作是一系列的图像，每一幅图像都是某一时间间隔内的人群流。前3帧用于预测下一帧，该模型由两层ConvLSTM层和一层卷积层组成。

ST-ResNet：时空残差卷积网络，在节点流量预测方面显示出最先进的性能。

MRF：基于马尔可夫随机场的全市流量预测模型，该模型利用所有单个区域的流量、区域之间的过渡以及外部因素(例如，天气)。

MDL使用TensorFlow和Kera实现，并通过反向传播和ADAM[18]优化进行训练。

 

3. 与其他模型的性能比较实验

             

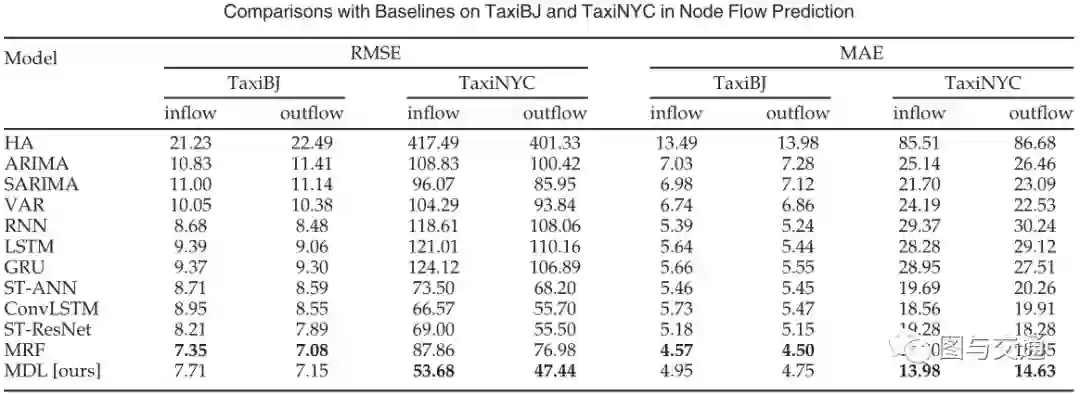
上表显示了TaxiBJ和TaxiNYC节点流量预测的RMSE和MAE。我们可以观察到，MDL和MRF始终优于所有其他基线。具体地说，MDL在TaxiNYC上的性能明显好于MRF。在数据集TaxiBJ上，MDL具有与MRF竞争的结果。原因可能是TaxiNYC比TaxiBJ大3倍。换句话说，MDL在大数据上比MRF有更好的性能。具体来说，以TaxiNYC的流量预测为例，RMSE的结果表明，MDL比HA好87%，比ARIMA好50%，比SARIMA好44%，比VAR好48%，比ST-ANN好26%，比RNN好54%，比ST-ResNet好22%，比ConvLSTM好19%。

             

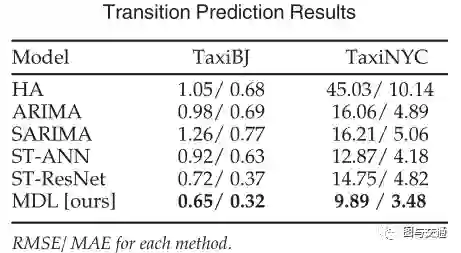
上表给出了TaxiBJ和TaxiNYC的边缘流预测的均方根误差(RMSE)和均方根误差(MAE)。过渡预测任务的实验非常耗时。主要在MDL和HA、ARIMA、SARIMA、ST-ANN和ST-ResNet上进行实验，结果表明MDL的性能优于其他算法。

 

4. 组件性能测试实验

             

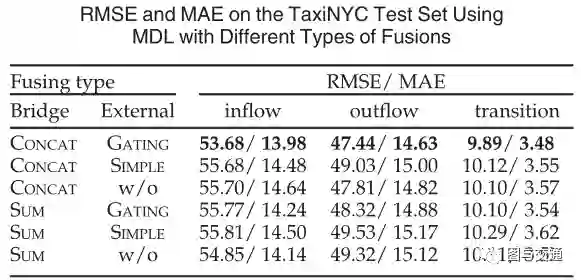
为了耦合NODENET和EDGENET，我们在前面介绍了Concat融合。还有一种直接的融合方法是sum融合。需要注意的是，SUM要求两个潜在特征地图具有相同的形状。对于外部因素的融合，可以选择以下方式之一：门控融合、简单融合也是就是sum或不使用(即w/o)。对所有变体使用相同的超参数设置(例如，训练迭代次数)。我们可以观察到，CONCAT+GATING方法的性能优于基于RMSE和MAE的其他方法。

             

             

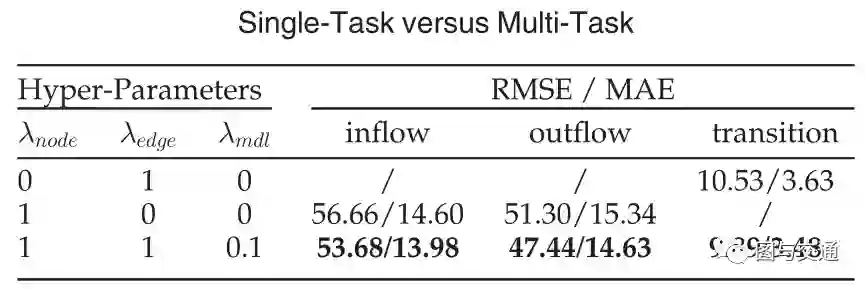
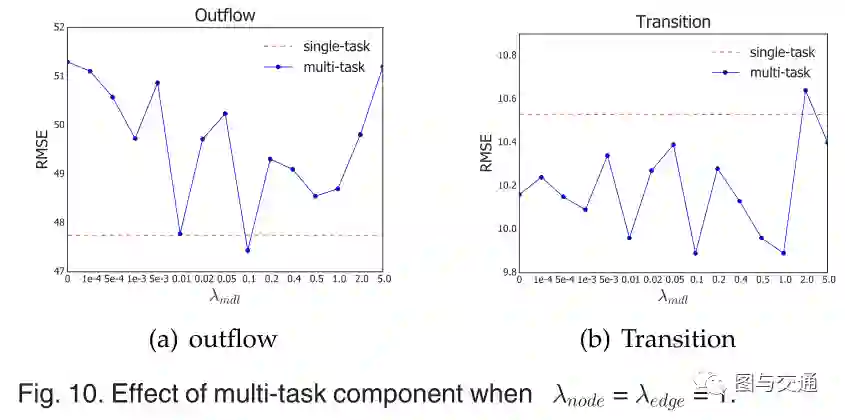
表和图10显示了我们的多任务组件对最终实验性能的影响。从表格和图表可以看出，过渡流预测任务在大多数情况下都可以改进，当node=edge=1和MDL=0.1时，我们的多任务模型取得了最好的性能，在这种情况下，两个任务都比两个单任务获得了更好的结果，这证明了我们的多任务部分可以相互促进每个任务的性能的有效性和可靠性。

             

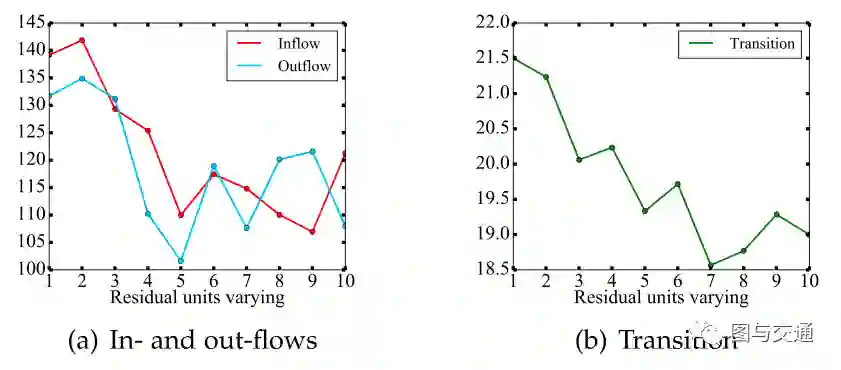
上图刻画了网络深度对TaxiNYC(3个月数据)的影响。随着网络的深入(即卷积数目的增加)，模型的均方根误差(RMSE)首先降低，这表明网络越深往往结果越好，因为它不仅可以捕捉空间上的近依赖关系，而且可以捕捉到远距离依赖关系。然而，当网络越深，RMSE越大，表明训练过程变得更加困难。

 

             

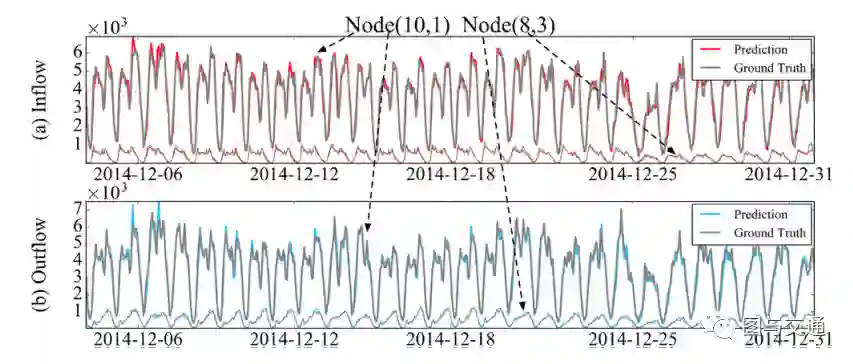
描述了两个节点对照2014年最后4周纽约市(NYC)的实际情况，对我们的MDL在未来一小时内的预测结果。具体地说，（10，1）节点的流量总是高于（8，3）节点的流量。可以观察到，模型在跟踪纽约市两个节点的交通流的地面真实曲线(包括突变)方面是非常准确的，这证明了所提出的模型的有效性。

 

6. 总结

提出了一种新的多任务深度学习(MDL)框架，用于同时预测时空网络中的输入/输出流(节点流)和跃迁(边流)。MDL不仅可以处理预测中的复杂性和规模性问题，而且可以相互加强对各种类型流量的预测。此外，MDL能够捕获空间相关性(近距离和远距离)、时间相关性(距离、周期、趋势)和外部因素(如事件和天气)。在北京和纽约的两个真实数据集上对MDL进行了评估，取得了明显好于11种基本方法的性能。

 

对于这篇论文来说，给自己的启示也有不少：

• 同一数据能够从不同角度来挖掘出有用的信息，不同信息之间可相互促进；

• 损失函数的设计，P,Q的引入，以及对两者的结合。

 

7. 参考

• Short-term traffic flow prediction with Conv-LSTM--2017WCSP

• Diffusion Convolutional Recurrent Neural Network: Data-Driven Traffic Forecasting--2018ICLR

• T-LSTM: A Long Short-Term Memory Neural Network Enhanced by Temporal Information for Traffic Flow Prediction--2019IEEE ACCESS

• City-Wide Traffic Flow Forecasting Using a Deep Convolutional Neural Network--2020SENSORS

• Spatio-Temporal Graph Convolutional Networks: A Deep Learning Framework for Traffic Forecasting--2018IJCAI

• T-GCN: A Temporal Graph Convolutional Network for Traffic Prediction--2019ITSS

• Attention Based Spatial-Temporal Graph Convolutional Networks for Traffic Flow Forecasting--2019AAAI

• Multi-Range Attentive Bicomponent Graph Convolutional Network for Traffic Forecasting--2020AAAI

• Deep Spatio-Temporal Residual Networks for Citywide Crowd Flows Prediction--2017AAAI

• Revisiting Spatial-Temporal Similarity: A Deep Learning Framework for Traffic Prediction--2019AAAI

• Deep Spatial–Temporal 3D Convolutional Neural Networks for Traffic Data Forecasting--2019ITSS

• Flow Prediction in Spatio-Temporal Networks Based on Multitask Deep Learning--2020TKDE

• 
  

 

正文结束