CS224W-11 成就了谷歌的PageRank

  众所周知(并不是)，谷歌最早是依靠搜索引擎起家的，而PageRank作为一种网页排序算法为谷歌的发展立下了汗马功劳。可以说，没有PageRank就没有今天的谷歌。

本次课程的主题包括：

1. Web structure
2. Pagerank推导和计算方式
3. 应用：Graph Search（个人认为反而是重要的部分）

1. Web Structure

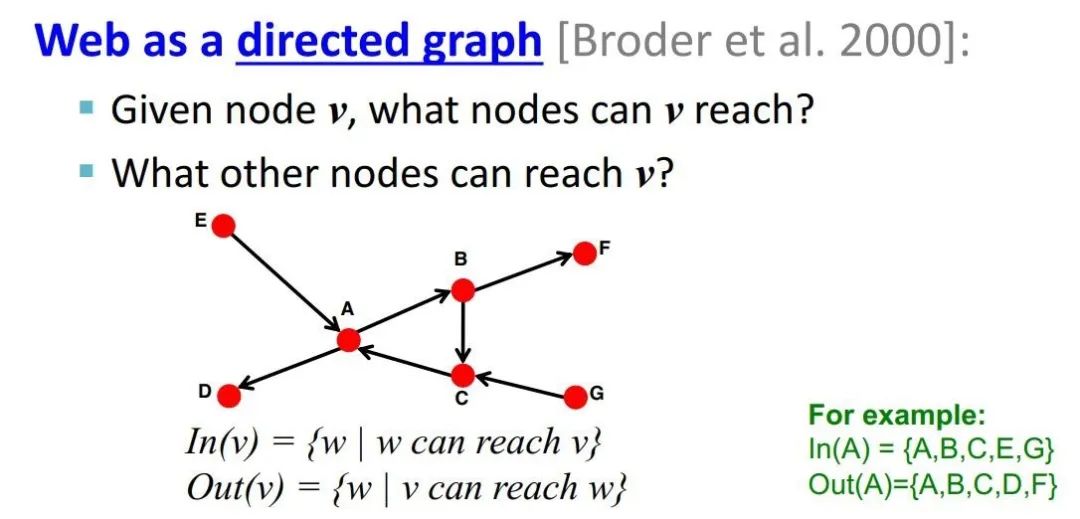
1.1 定义：有向图

: 所有能够到达v的节点集合

：所有v能够到达的节点集合

img

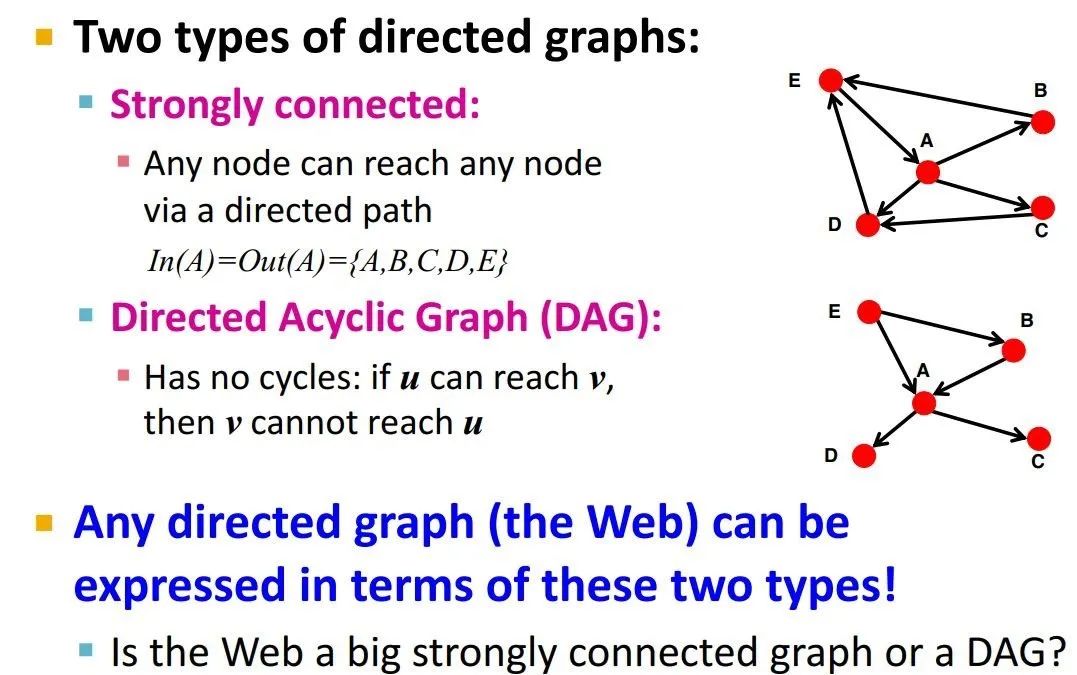
有向图的两种类别：

strongly connected：节点间是互通的，能够通过有向路径实现互达

directed acyclic graph：有向无环图，u可以达到v，但v不能到达u

img

Strongly connected component

1. 这个集合内节点可以互达
2. 这已经是最大的满足这种要求的集合，不能更大了

每一个有向图都是在SCC上构成的DAG

意思是说，如果把有向图中能够互达的节点集合揉成一个新结点，那么就是一个DAG了

img

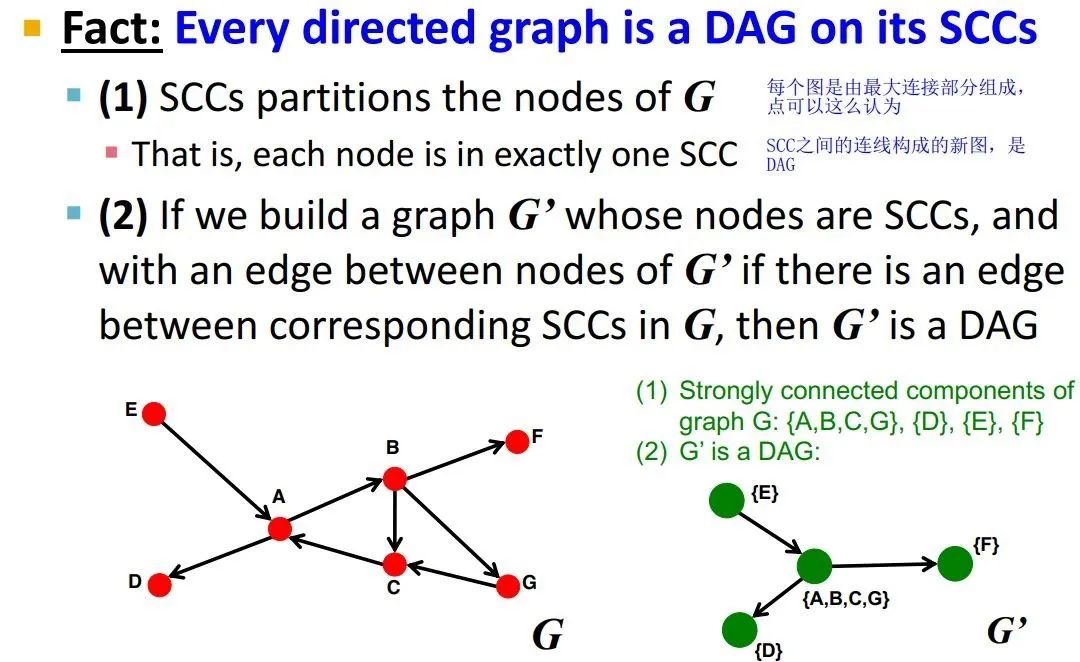
问题来了：想看看真是Web网络，是如何在其SCC上构成整个DAG图的？

1. 首先，对于一个节点v，如何找到包含这个v的SCC？

定义：

是G的反向图

img

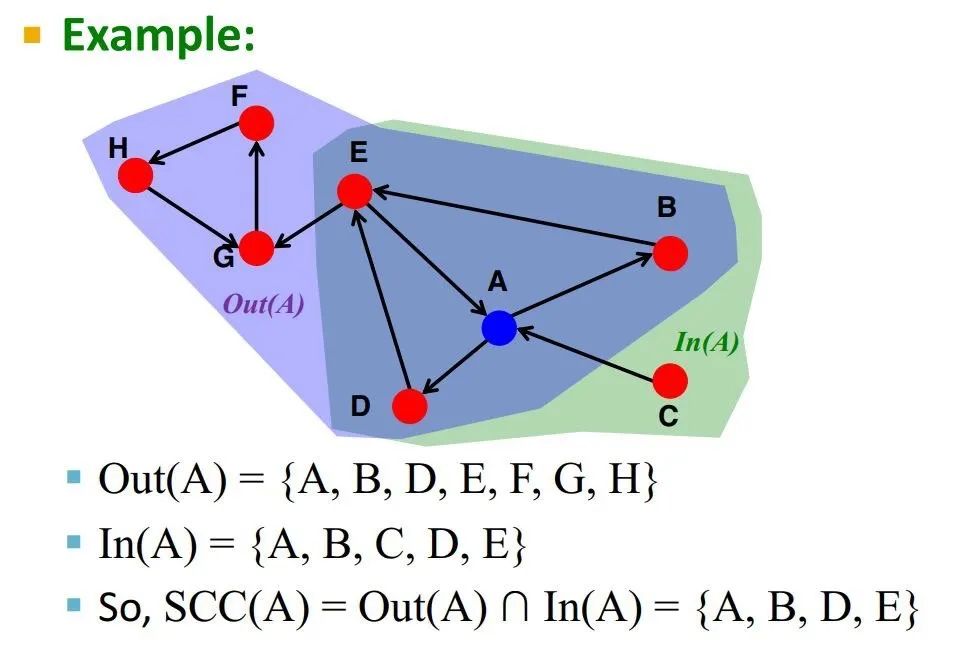
2. 实验结果

• 数据来源：爬取的网络结构，2.03亿 urls，15亿links
• 方法：任意节点v，使用BFS策略（宽度优先）计算In(v)和Out(v)
• 观察结果：BFS策略要么访问极少的节点，要么可以访问居多的节点

img

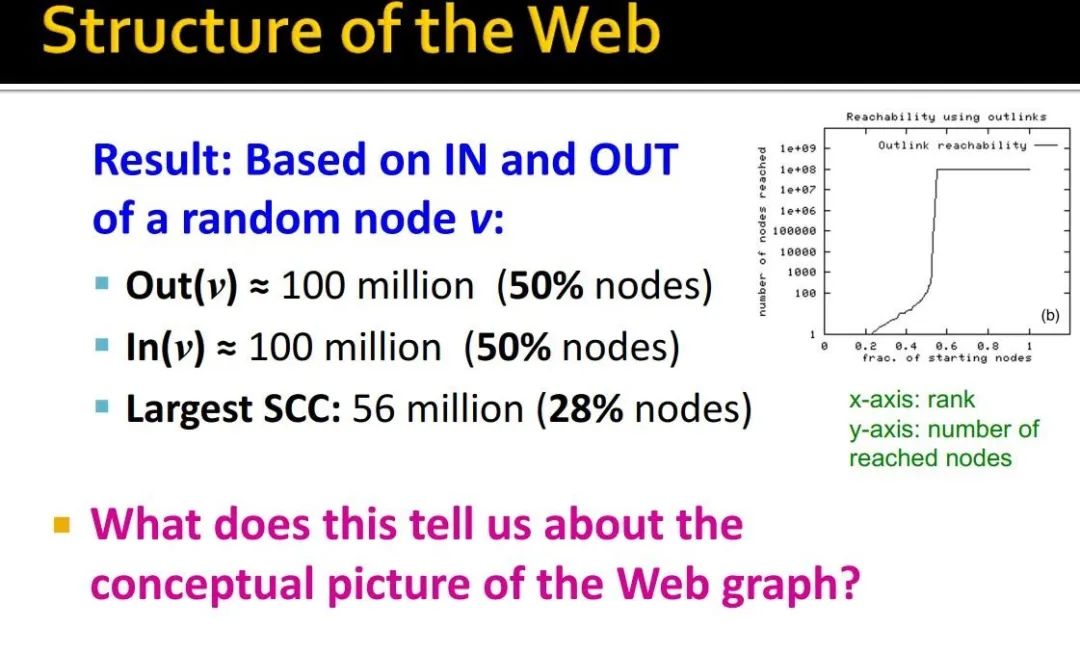
说明，网络结构是一个领带形式的玩意。

img

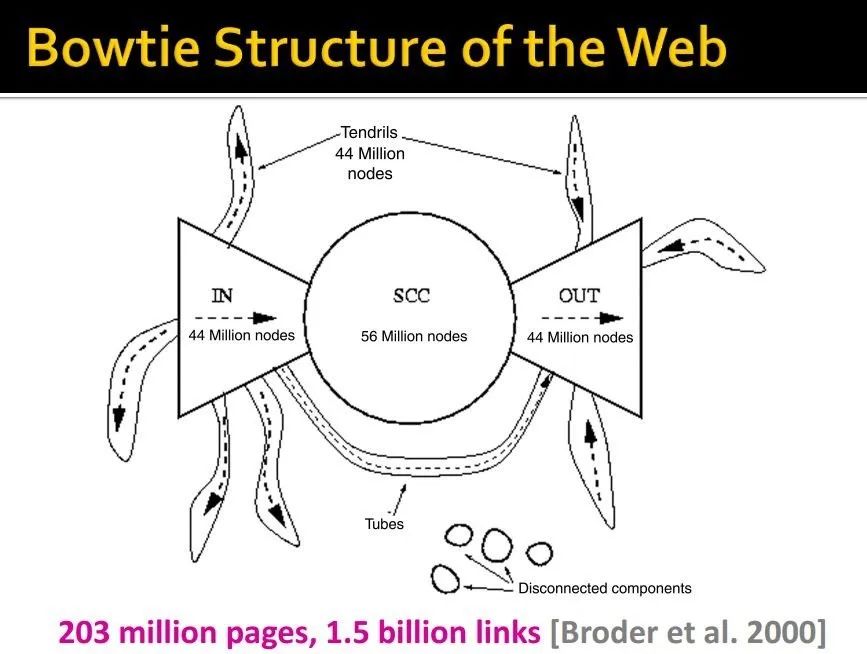
2. Ranking nodes on the graph

Intuition：网络中不同节点的重要度肯定是不同的，stanford vs 野鸡大学

所以，我们要排序！

rank the pages using the web graph link structure

Link Analysis Algorithms

• pagerank
• personalized pagerank
• random walk with restarts

PageRank

Idea：将link视为votes，链接越多越重要

还有一个问题，所有链接都一样吗？

那肯定不行啊，杀人游戏中，警长还有两票的投票权呢

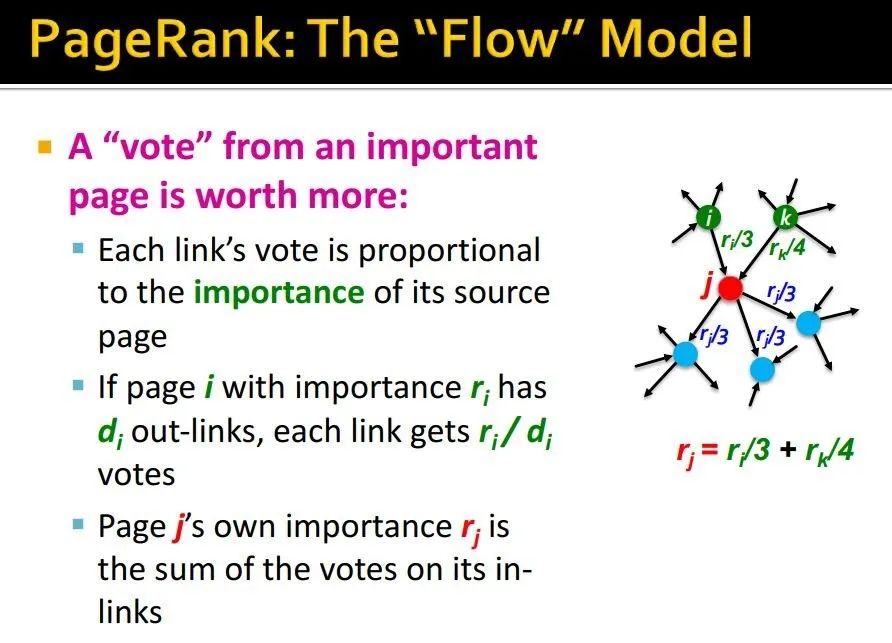
从重要节点投出的票会更加重要！

那怎么分配链接上的权重呢？平均

• 对于page with importance ,有 个外向连接（出度），那每个链接得到的投票权为：
• 对于节点 j ，其重要度就是所有指向它的投票权之和：

img

img

用矩阵定义这种形式，引入邻接矩阵M

如果 ，   的出度为 ，那么

M的列和为1，表示所有从j出去的投票权

rank vector r：每个节点的重要度

矩阵形式：

img

接下来的论述是，设想是一个surfer在这样的web上一直随机游走，最后停留在各个页面上的概率

这样论述的目的在于得到一个概率形式：

那么 就是最后的稳态概率，对应意义说各个节点重要度也会收敛起来

这可以有两个解释：

1、马尔可夫过程的收敛

其实给定矩阵 ，计算   的过程就是一个重复的过程

相当于是一个马尔可夫链最后的收敛状态

2、特征值分解

对比一下，其实就是特征值为1的特征向量！

工业上如何求得r呢？——Power Iteration Method

迭代过程很简单：三步

• 初始化：
• 迭代：
• 终止条件：

示例：

img

写到这里，不得不思考几个问题：

• 这个计算模式，它最后收敛吗？
• 如果能够收敛，是否收敛到我们想要的值？
• 结果合理吗？

Pagerank有两个小问题需要解决

1、dead ends：有些网页不能往外链接了，也就是断头路

如图，所有重要度都变成0

img

解决方式：以概率1.0转移到其他节点

需要调整邻接矩阵

img

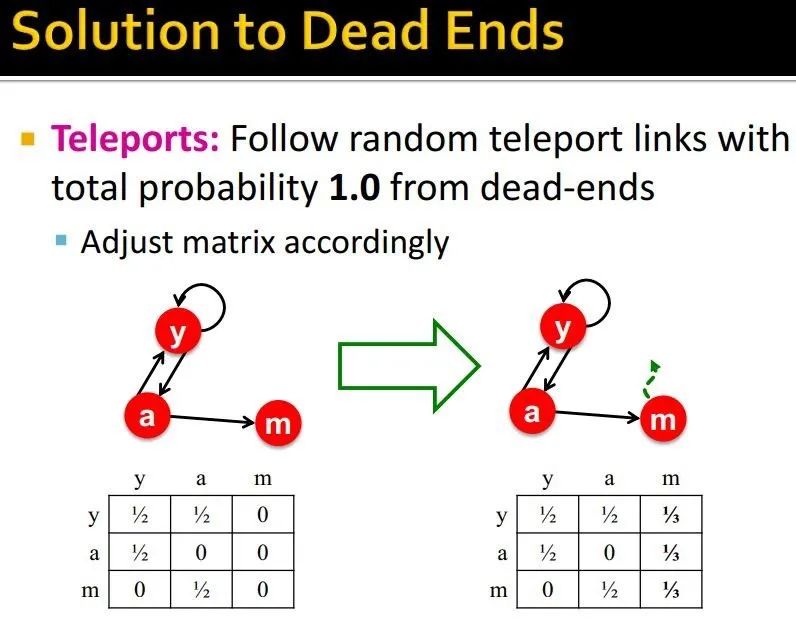
2、spider trap：陷入局部循环了，一直在一个圈里打转，导致importance计算不正常

如图，a重要度变成0，b成了1

img

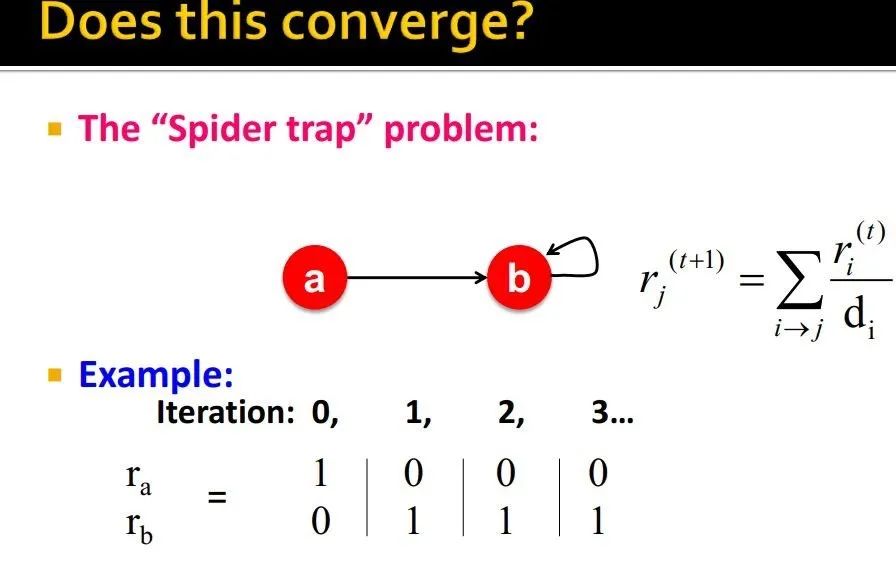
解决方式：跳出这种问题

• 概率 的可能继续随机走
• 概率 的可能跳转到其他随机页面

值在0.8-0.9之间

如何，在经历几步后，能够瞬移出spider trap

img

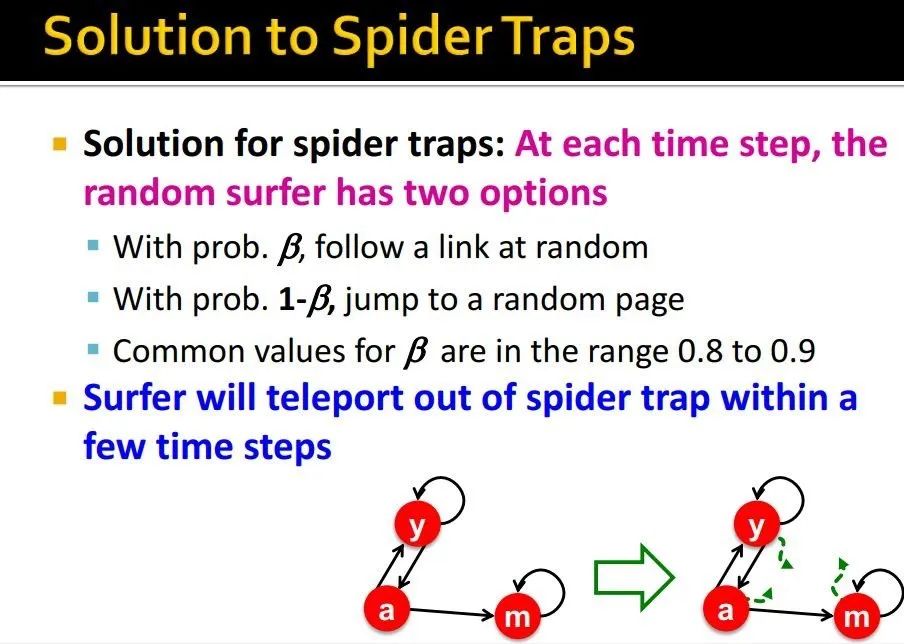
为什么teleport能够解决问题呢？

• spider-trap不是实际的问题，只是会导致我们求得值不准确
• dead ends才是问题，会导致列和不为1，不满足我们的assumption，所以需要调整M

综合起来，就是random teleports

• 概率 的可能继续随机走
• 概率 的可能跳转到其他随机页面

PageRank equation：[Brin-Page, 98]

Google Matrix

取0.8~0.9 (平均跳转5次即可)

img

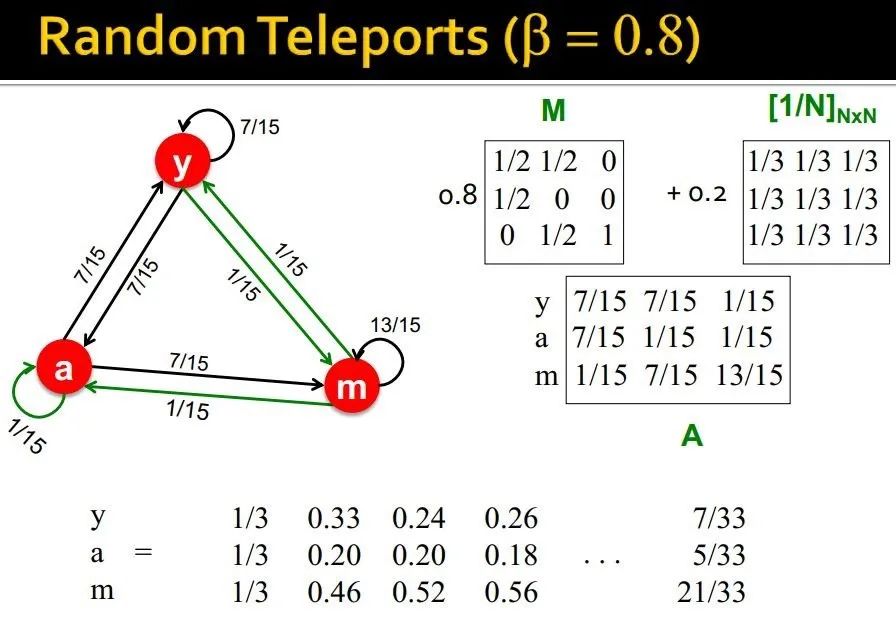
实际上怎么计算PageRank呢？

全部输入内存里，太占空间了，并且矩阵 实际上稀疏矩阵，所以，实际上

1. 先计算  
2. 再将 叠加到 中

如果存在dead ends，那么M的列和不为1, , 这时候需要renormalize

img

这个图很形象

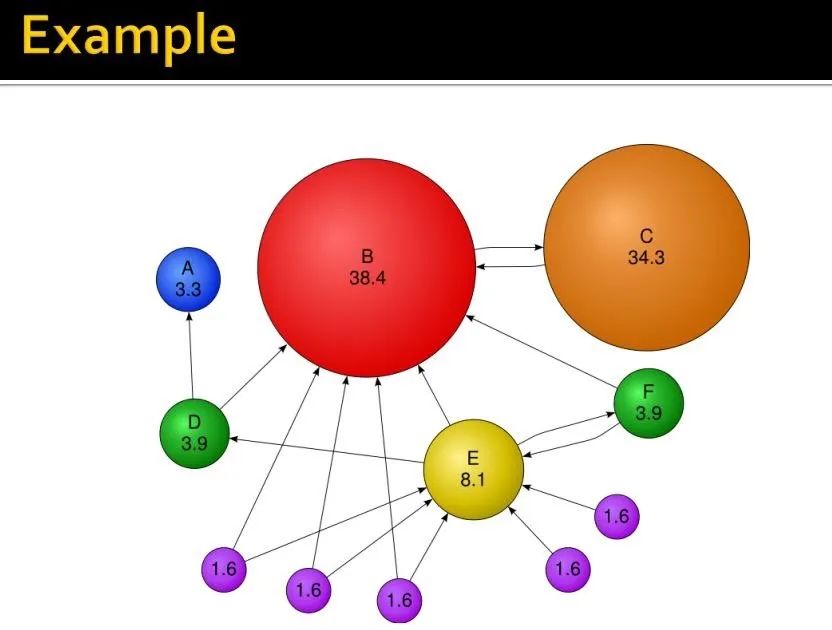
Random Walk with restarts and personalized PageRank

I like it, 不然都不会写这一章的笔记了

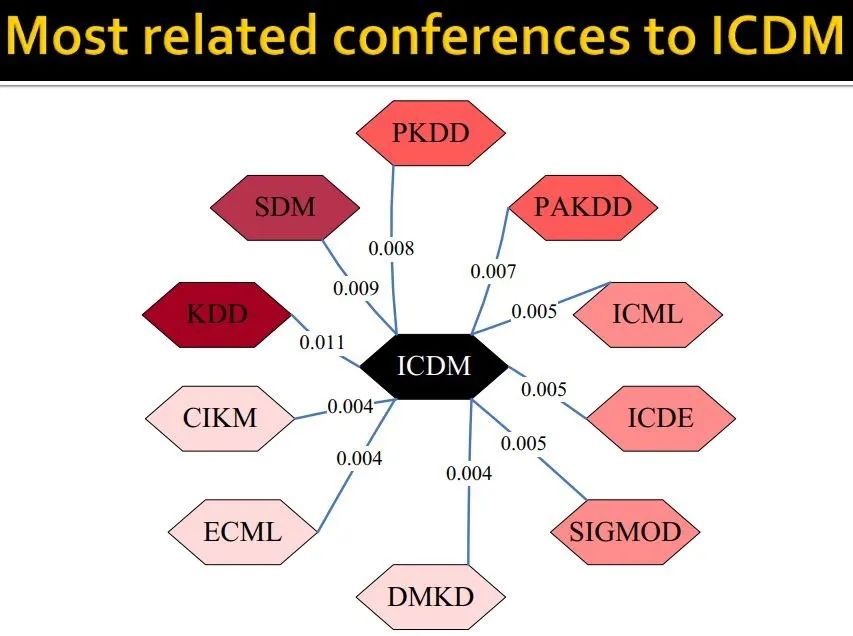
给定一个conference-to-authors graph（这个图在异质图处理里经常有）

推荐问题

img

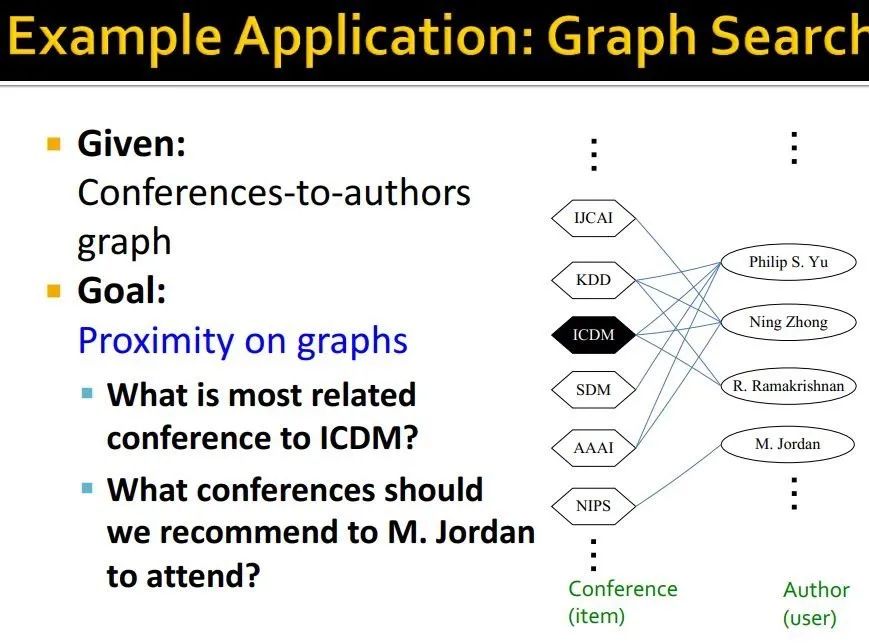
转化为二部图，user-item graph

这其中一个问题，就是要找到一个节点，与其最相似的邻居们

Node proximity measurement

如果找的效果好的话，embedding也会在一起，那么协同过滤推荐的策略也会提高性能

img

img

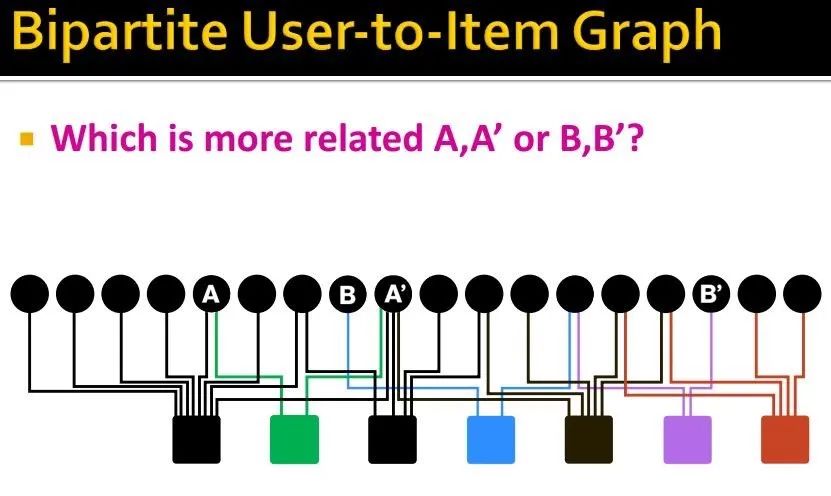
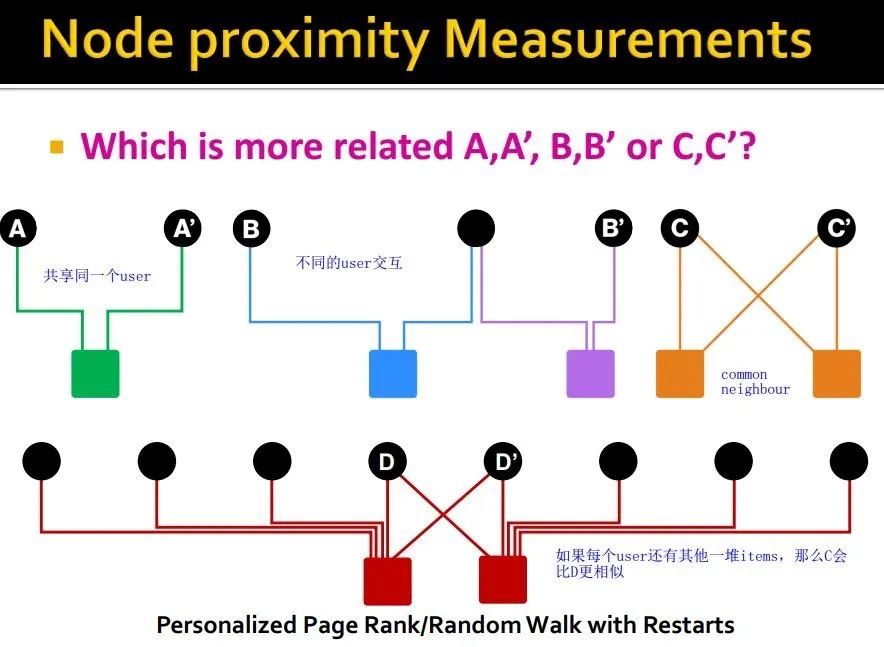
如何更好的刻画图上节点间的相似性呢？

• rank nodes by 重要度
• Personalized PageRank：ranks proximity of nodes to the teleport nodes S
• random walks with restarts：要跳转的时候，直接跳回起始位置

img

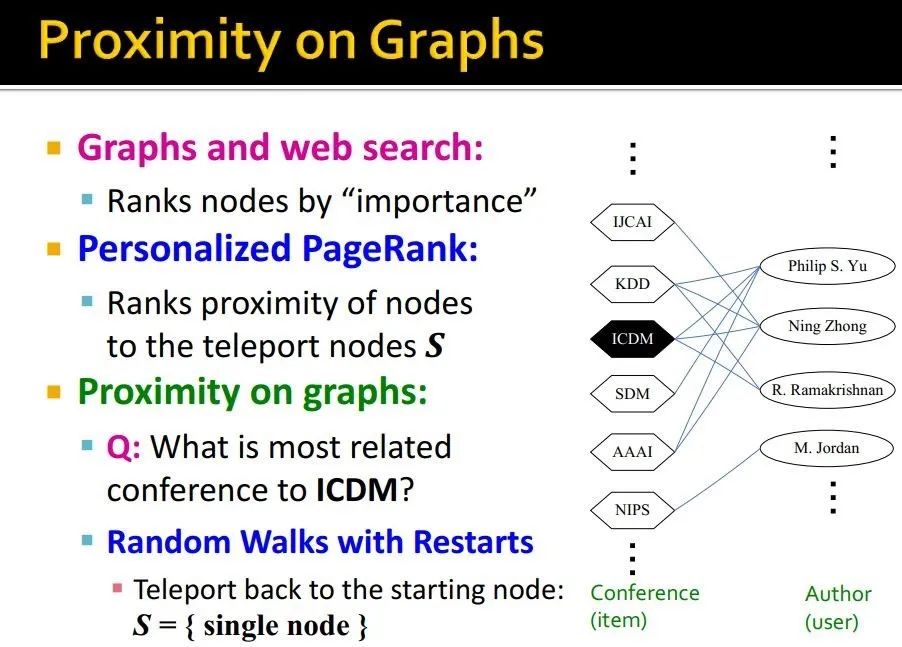
讲道理，可以用之前说的power iteration method计算。

但实际上，只用random walks来模拟这个过程就可以了。

这个方法应用的非常广泛，许多顶会论文也会使用这种方法。

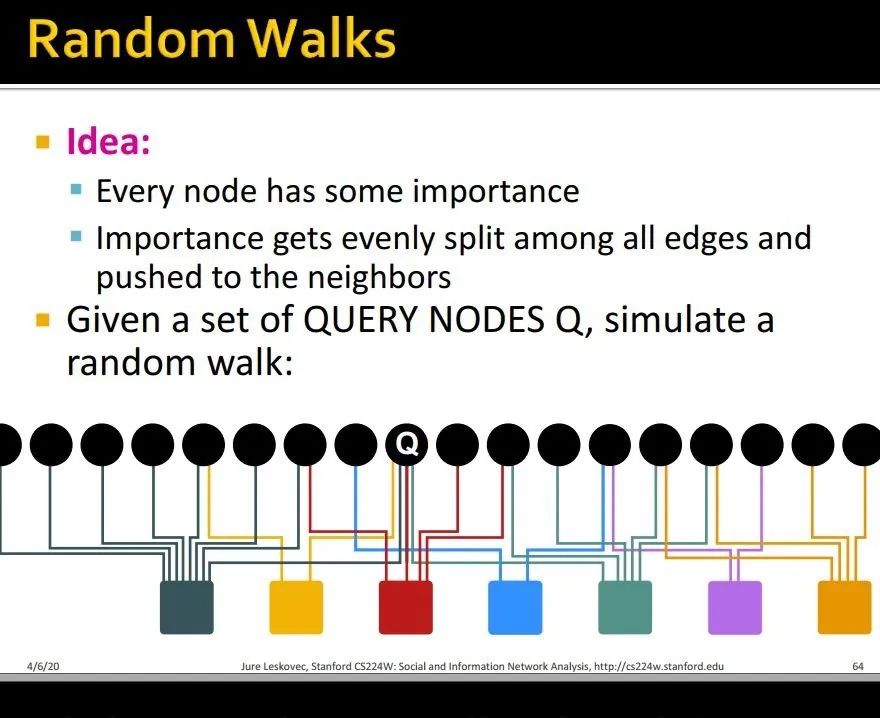
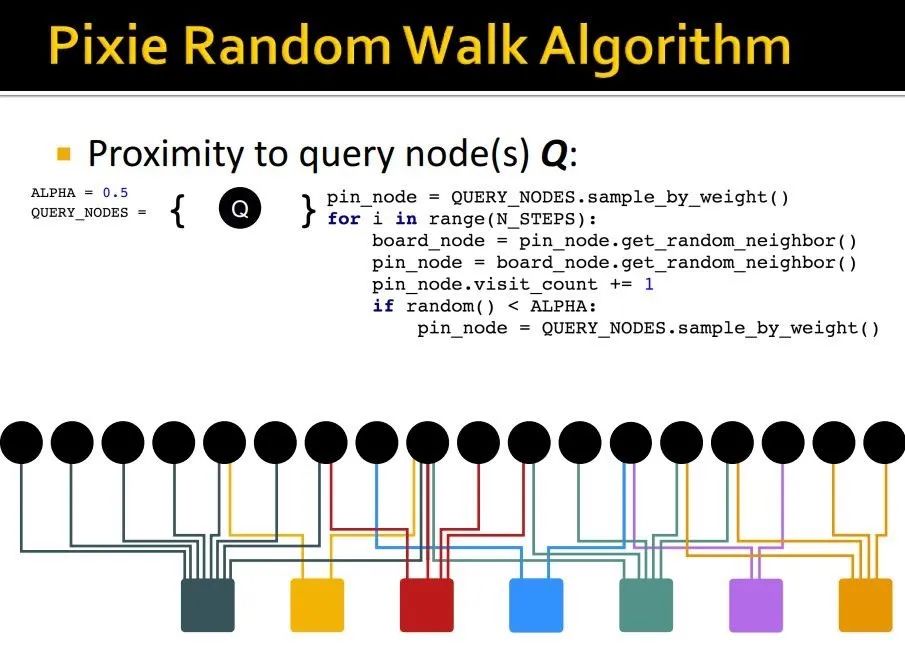
步骤：给定query nodes，我们进行如下操作：

1. 向随机的邻居进发，记录每个节点被访问次数
2. 有概率ALPHA的可能跳回到某个query nodes
3. 所有访问过的节点中，访问次数最高的，就是和query nodes有最大近似度的节点集合。

优点：考虑了网络结构的许多特性

• multiple connection
• multiple paths
• direct and indirect connections
• degree of the node

img

img

img

img

Summary

1. Normal PageRank

• 随机跳转到任意节点
• 所有节点达到概率相同

2. Personalized PageRank

• 跳转到一组特定主题的节点上/网页上
• 节点到达概率是不同的

3. Random Walk with Restarts

• 总会跳转到起始节点

img

更多关于图神经网络/图表示学习/推荐系统, 欢迎关注我的公众号 【图与推荐】