Deepmind最新研究:从图表示学习看算法推理
新智元报道
新智元报道
来源:deepmind等
编辑:雅新
【新智元导读】在上周三ICLR 2020大会中,来自Deepmind的研究人员Petar Veličković介绍了用算法推理的图表示学习最新研究。该研究提出了主要邻域聚合(PNA),并通过实践证明了使用多个聚合策略同时提高了GNN的表现力。「新智元急聘主笔、高级主任编辑,添加HR微信(Dr-wly)或扫描文末二维码了解详情。」
由于图的不规则性,传统的深度学习算法在处理复杂的图时面临着巨大的挑战。
近年来,人们对深度学习方法在图上的扩展有着浓厚的兴趣,由此一个新的研究热点——图神经网络(GNN)应运而生。图神经网络在算法推理能力上有着不可估量的潜力,甚至有望成为下个AI拐点。
上周的ICLR 2020大会中,来自Deepmind的研究人员Petar Veličković主要介绍了用于算法推理的图表示学习最新研究。

图表示学习
GNN 的出现,给图表示学习带来了新的建模方法。图表示学习是深度学习的一个方向,是一种无监督学习,其核心是研究图数据的表示。以 DeepWalk、LINE 和 node2vec 为代表的图表示学习技术得到广泛地应用。
为什么我们要通过图来表示学习?是因为很多数据都是图结构,例如社交网络、经济网络、生物医学网络、信息网络、互联网、神经网络等。
图数据中蕴含着丰富的结构信息,然而因其内在关联而产生的一种非线性结构,在补充刻画数据时,给数据学习带来了巨大挑战。因此,图表示学习在此就会发挥巨大的作用。
它具有两个重要作用,一是将图数据表示成线性空间中的向量;二是为之后的学习任务奠定基础。
GNN表现力不够强
图神经网络(GNN)在过去十年中一直是活跃的研究领域,同时图表示学习取得了巨大的突破。但是,由于缺乏标准化的基准和表现力的理论框架,新型图神经网络的有效性很难让人理解。
实际上,该领域的大多数工作都集中在改进一组图形基准上的GNN架构,而没有评估其网络能否正确表示图的结构特性。
直到最近,才有关于各种GNN模型表现力的重大研究,主要集中在同构任务和可数特征空间上。但是,这些主要侧重于区分不同的图形拓扑能力上,而在了解它们能否捕获并利用图结构的基础特征上所做的工作很少。
或者一些工作侧重于使用光谱域将卷积神经网络(CNN)推广到图形,这是Bruna等人首先提出的。为了提高光谱分析效率和改善模型的性能,Chebyshev多项式诞生,后来推广到Cayley滤波器。
在本文研究工作中,研究人员着眼于不同GNN模型理解光谱分解某些方面的能力,即拉普拉斯图和光谱半径,因为它们构成了图的光谱特性的基本方面。虽然光谱特性和滤光片没有在此次的架构中明确编码,但功能强大的GNN仍然能够有效地学习。
研究发现:主要邻域聚合(PNA)
先前经典图论工作着重于评估GNN模型在单个任务上应用的性能,如最短路径,图矩或旅行商问题。
而本文研究者们采用了不同的方法开发多任务基准,同时包含节点级和图形级的问题。他们还特别观测了每个GNN预测单源最短路径,离心率,拉普拉斯特征的能力,连通性,直径和光谱半径。其中许多任务基于使用动态算法编程,因此非常适合于GNN的研究。
Petar表示,「我们相信这项多任务方法可确保GNN能够同时理解多种特性,这是解决复杂图形问题的基础。而且,任务间有效地共享参数,表明了其对图形的结构特征有更深入的了解。此外,我们通过在更大尺寸的图形上进行测试来探索网络的泛化能力存在于训练集中。」
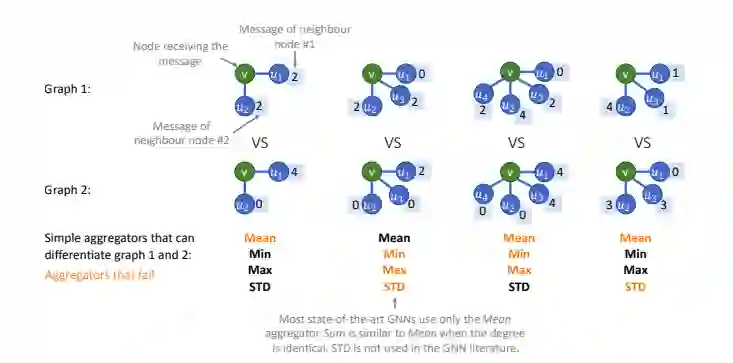
通过假设当前的GNN的聚合层从节点邻域进入单层无法提取足够的信息,这限制了它们的表现力和学习能力。实际上,最近的工作表明不同的聚合器在不同的任务上表现更好。由于不能正确识别邻域,同时也无法可靠地找到子结构,GNN并不能很好地学习节点集群。
研究者们首先对引入不可数多集注入性问题提出解决方案,从数学上证明对多种聚合的需求。然后,他们提出了标度的概念,作为总聚合概括,它允许网络基于每个节点的程度放大或衰减信号。结合以上内容,研究者又设计了主邻域聚合(PNA)网络,并通过实践证明了使用多个聚合策略同时提高了GNN在图论问题上的性能。
Petar把目前现有研究中的CNN算法分为了三个级别 Unit-level, Step-level, Algo-level

作者同时分析了GNN的理论框架扩展到了连续的特征,并证明了在这种情况下需要多个聚合器。通过呈现标度来聚合,并建议使用对数标度。
针对以上所有因素,作者提出了一种由多个聚合器和标度组成的「主要邻域聚合」。为了理解GNN捕获图结构的能力,并提出了一种新颖的多任务基准以及用于解决它的编码过程解码结构。

Petar表示「我们认为,我们的发现构成了建立GNN具有表现力模型层次结构的一步,从这个意义上讲,PNA模型似乎优于GNN层设计中的现有技术。」
「算法推理是图形表示学习一个令人兴奋的新领域。」