向希格斯老大二呼夸克！

2018 年 7 月 25 日 中科院物理所

本文经「原理」（微信公众号：principia1687）授权转载，

禁止二次转载。

自2012年探测到希格斯玻色子以来，欧洲核子研究中心（CERN）的大型强子对撞机（LHC）在持续积累数据的过程中，不断取得稳步进展。在最近的两个结果中，他们确定了两个最重夸克的质量来源。

大型强子对撞机的ALICE实验的参观中心。| 图片来源：Jon Butterwood

每个原子的中心都有一个原子核，而构成原子核的最小单元便是夸克。“夸克”一词是诺贝尔物理学奖得主盖尔曼（Murray Gell-Mann）取自乔伊斯（Jame Joyce）小说《芬尼根的守灵夜》中的一句“向麦克老大三呼夸克（Three quarks for Muster Mark）”。在已知的物质世界中，没有什么东西是比夸克更小的。事实上，据我们目前所知，夸克是无限小的。

如果你认为粒子无限小这个概念相当难以理解，那么还有更加匪夷所思的，那便是无限小的夸克竟然还具有质量。而且在已知的六种夸克中，有些夸克还具有很大的质量。顶夸克的质量几乎和一个钨原子的质量相当。在粒子物理学的微小尺度上，钨原子是一个巨大的、不规则的物体。底夸克的质量比氦原子大一点，以粒子尺度的标准来看这仍然相当可观。

夸克粒子如何具有质量这一问题，使理论物理学家非常困扰。为了解决这一问题，物理学家预言，在宇宙中应该存在一个新的量子能量场，它存在于宇宙中的任何地方。粒子可以通过与这个场相互作用而获得质量。

正如光子是电磁场中的量子涟漪一样，新的“质量”场可以激发一种新的粒子，也就是希格斯玻色子。希格斯玻色子是以提出这一想法的其中一位理论物理学家的名字命名的。2012年，CERN宣布发现希格斯玻色子，为这些惊人的想法极大地增添了可信度。

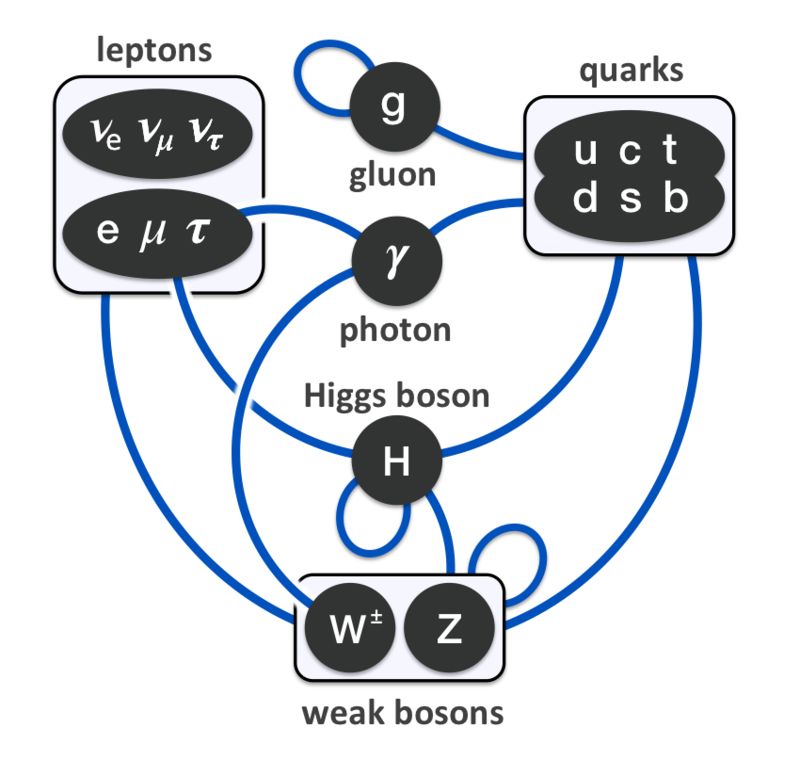
○ 标准模型中粒子间的相互作用 | 图片来源：Wikipedia

然而，2012年首次探测到希格斯玻色子并没能向我们展示所有的信息。辨别出与夸克的相互作用是一个很大的挑战，很大程度上是因为在LHC中碰撞的质子本身就充满了夸克，将质子撞击在一起会导致仪器中充满大量的夸克——这会产生大量的背景噪音，使得希格斯粒子的信号难以辨别。

随着更多的碰撞被记录，我们可以用纯熟复杂的噪声抑制技术来挑选那些信号。

今年4月，科学家首次清晰地观测到了希格斯玻色子与质量最大的顶夸克的相互作用。就在几周前，ATLAS实验的科学家又宣布，他们以统计显著性为5σ（任意但重要的）的水平，观测到了希格斯粒子与底夸克的相互作用。5σ意味着信号由本底噪声导致的概率只有千万分之三。

○ 2018年7月9日，运行于于CERN大型强子对撞机LHC上的ATLAS实验探测到了希格斯粒子衰变为底夸克对（H→bb）的过程。| 图片来源：atlas.cern

这些结果与认为希格斯玻色子的场赋予了底夸克和顶夸克质量的观点是一致的。即便精确度不是很高，然而随着我们收集更多数据以及减少实验的不确定性，还会出现更多惊喜。我们真的非常期待一些惊喜，因为在物理学中，有许多重要问题是目前的理论无法解答的。这些（或其他）测量之间的差异可能是一个更大、更好、更有效理论的线索。

也就是说，从LHC的海量数据中筛选出这些事件是一个巨大的成功。而我们已有的关于物质结构的最好理论，又一次通过了检验。总体而言，我们已经触碰到了物理学的顶端。

文：Jon Butterworth

译：二宗主

原文链接：

https://www.theguardian.com/science/life-and-physics/2018/jul/23/two-quarks-for-muster-higgs。

中文内容略有修改，仅供参考，一切内容以英文原版为准。

来源：原理