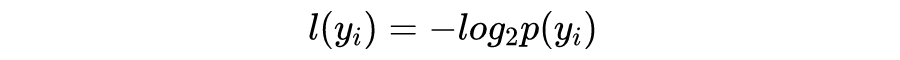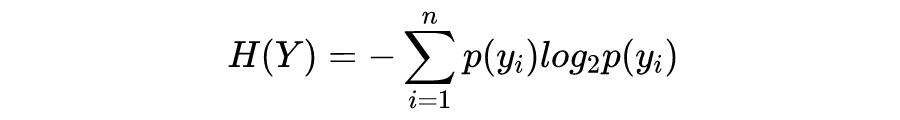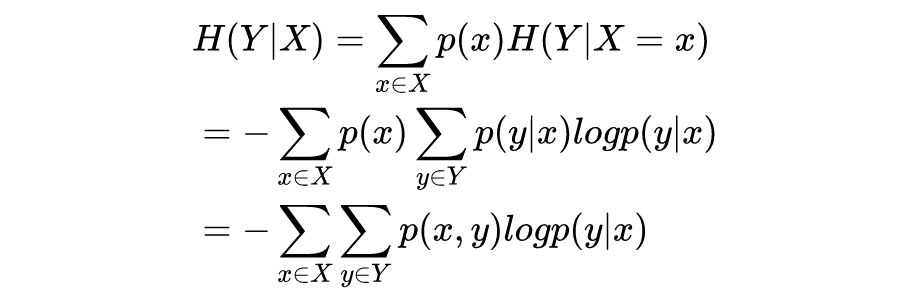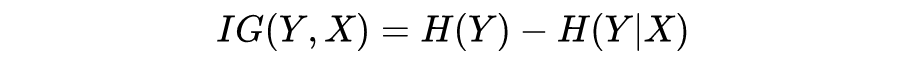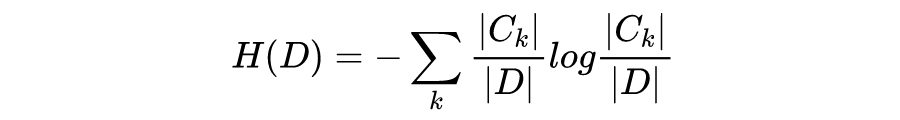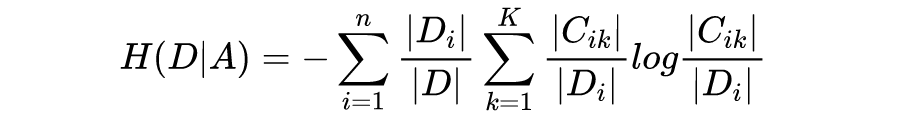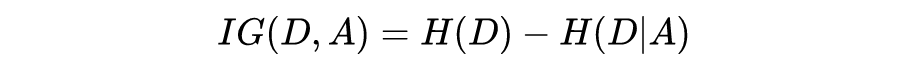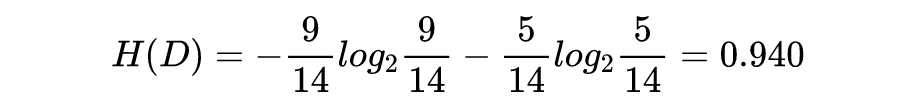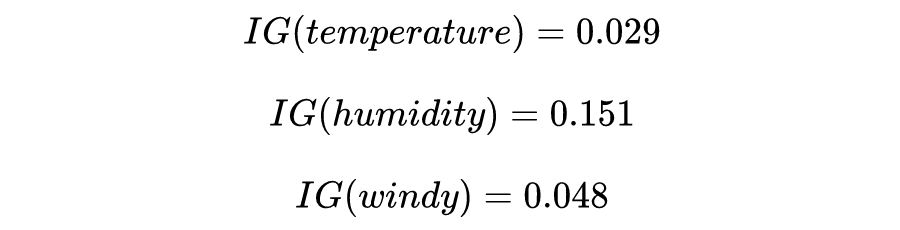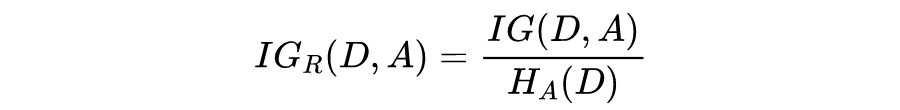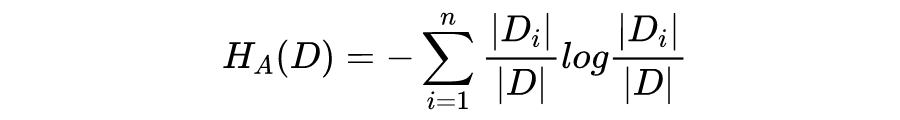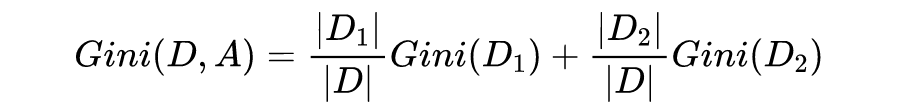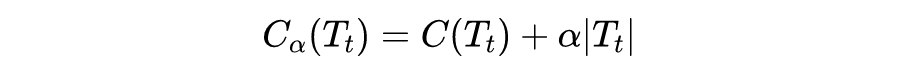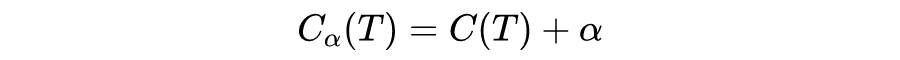决策树是如何选择特征和分裂点?
©PaperWeekly 原创 · 作者|贲忠奇
单位|便利蜂算法工程师
研究方向|推荐算法、反作弊

在解决回归和分类问题的时候,一般会使用 Random Forest、GBDT、XGBoost、LightGBM 等算法,这类算法因为性能好,被业界广泛采用。突然想到树类型的算法都需要明白一个基本问题,树是如何选择特征和分裂点的?其根本要追溯到决策树的种类,每种是如何划分特征和分裂点,以及如何剪枝的。
信息论基础
条件熵是在特征 X 给定条件下,类别 Y 的条件概率分布的熵对特征 X 的数学期望。
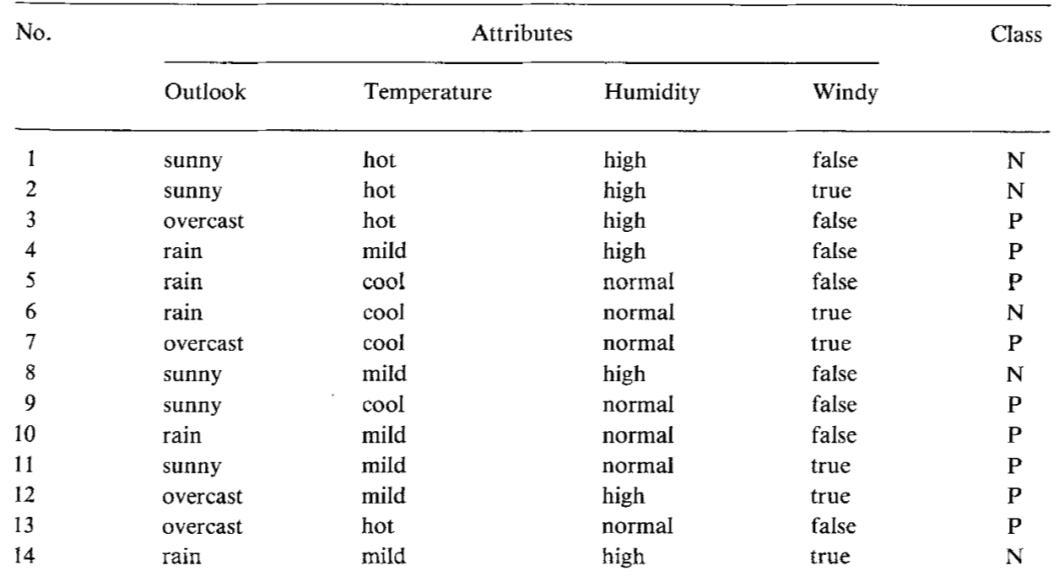
数据说明
在讲完一些信息论的基础知识的基础上,由于原始论文中公式的表示不是同一个体系,为了更加方便理解这三者,因此下文中三个算法的介绍都以下面数据集为基础。

ID3
4.1 算法思路
利用训练数据集 D 与特征 A 来表示信息增益的计算方式,那么需要以下几个步骤:
当 H(D) 的值越小,说明样本集合 D 的纯度就越高。
信息增益越大,说明用特征 A 来划分数据集 D,信息混乱程度越小。我们需要对样本的所有特征计算信息增益情况,选择信息增益大的特征来作为决策树的一个结点,或者可以说那些信息增益大的特征往往离根结点越近。
4.2 决策树生成过程
检测数据集中的每个子项是否属于同一分类:
if so return 类标签
else
寻找划分数据集的最好特征
划分数据集
创建分支节点
for每个划分的子集
调用函数createBranch并增加返回结果到分支节点中
retrun 分支节点
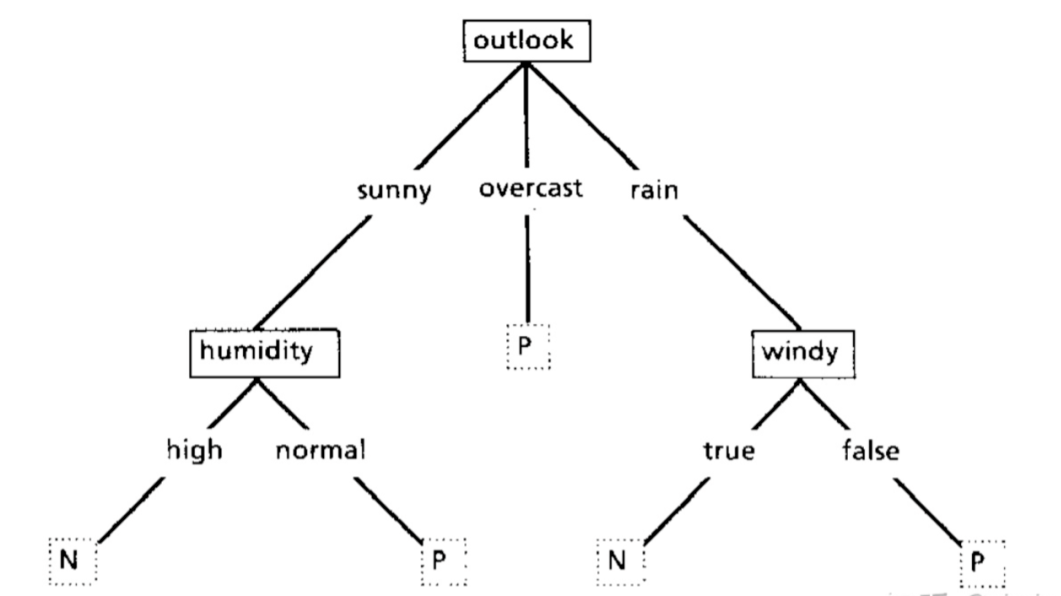
4.3 示例
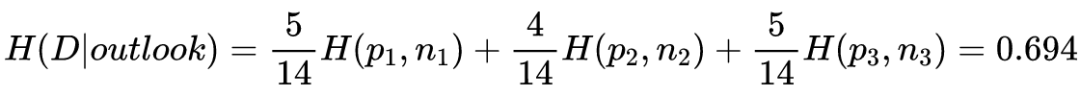
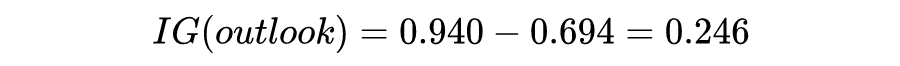
C4.5
CART树
6.1 CART数据集混乱程度衡量
6.1.1 CART分类树
6.1.2 CART回归树
6.2 树的生成过程
找到最佳的待切分特征:
如果该节点不能再分,将该节点存为叶节点
执行二元切分
在右子树调用createTree()方法
在左子树调用createTree()方法
那么如何找到最佳的待切分特征和特征值呢?
每个特征:
每个特征值:
将数据切分成两份
计算切分的误差
如果当前误差小于当前最小误差,那么将当前切分设定为最佳切分并更新最小误差
返回最佳切分的特征和特征值
6.3 树的剪枝
预剪枝过程相对简单,在生成树的过程中,如果某个特征和特征值切分的样本小于最小样本数或迭代误差下降值小于设置的最小下降值,就停止切分。预剪枝可以降低过拟合的风险并减少决策树的训练时间,但是也会带来欠拟合的问题。
基于已有的树切分验证集数据:
如果存在任一子集是一棵树,则在该子集递归剪枝过程
计算将当前两个叶节点合并后的误差
计算不合并的误差
如果合并会降低误差的话,就将叶节点合并

决策树算法小结
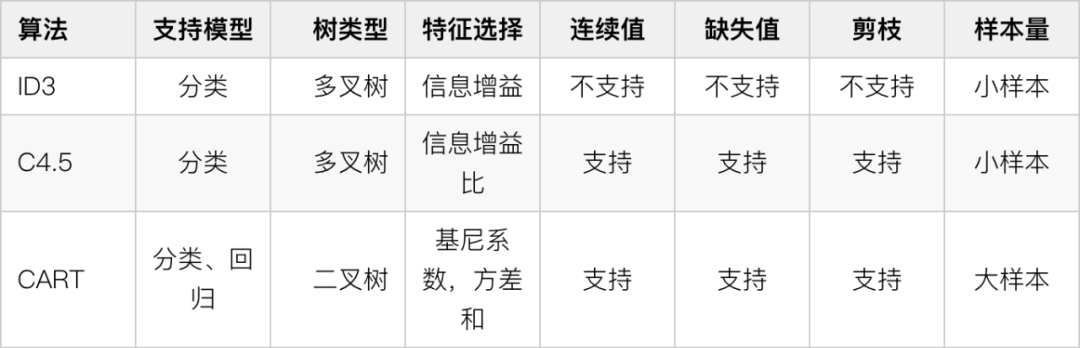
目前这三种算法都是一棵树中的特征来决定最后的结果,后来发展成一组树来决定最后的结果。如果这些树是并行投票,就是每个树的投票权重相同,形成了 bagging 类的算法,最有代表性的是 Random Forest;如果这些树是串行投票,每个树的投票权重不同,通过拟合残差的方式,形成了 boosting 类的算法,最有代表性的是 GBDT、XGBoost、LightGBM。
参考文献
[1] Leo Breiman, Jerome H. Friedman, Richard A. Olshen, Charles J. Stone.(1984).
[2] Classification And Regression Trees Quinlan1986_Article_InductionOfDecisionTrees
[3] C4.5: by J. Ross Quinlan. Inc., 1993. Programs for Machine Learning Morgan Kaufmann Publishers
[4]《机器学习实战》
[5] https://www.cnblogs.com/pinard/p/6053344.html
[6] 周志华西瓜书《机器学习》
更多阅读


#投 稿 通 道#
让你的论文被更多人看到
如何才能让更多的优质内容以更短路径到达读者群体,缩短读者寻找优质内容的成本呢?答案就是:你不认识的人。
总有一些你不认识的人,知道你想知道的东西。PaperWeekly 或许可以成为一座桥梁,促使不同背景、不同方向的学者和学术灵感相互碰撞,迸发出更多的可能性。
PaperWeekly 鼓励高校实验室或个人,在我们的平台上分享各类优质内容,可以是最新论文解读,也可以是学习心得或技术干货。我们的目的只有一个,让知识真正流动起来。
📝 来稿标准:
• 稿件确系个人原创作品,来稿需注明作者个人信息(姓名+学校/工作单位+学历/职位+研究方向)
• 如果文章并非首发,请在投稿时提醒并附上所有已发布链接
• PaperWeekly 默认每篇文章都是首发,均会添加“原创”标志
📬 投稿邮箱:
• 投稿邮箱:hr@paperweekly.site
• 所有文章配图,请单独在附件中发送
• 请留下即时联系方式(微信或手机),以便我们在编辑发布时和作者沟通
🔍
现在,在「知乎」也能找到我们了
进入知乎首页搜索「PaperWeekly」
点击「关注」订阅我们的专栏吧
关于PaperWeekly
PaperWeekly 是一个推荐、解读、讨论、报道人工智能前沿论文成果的学术平台。如果你研究或从事 AI 领域,欢迎在公众号后台点击「交流群」,小助手将把你带入 PaperWeekly 的交流群里。