NIPS 2017最佳论文出炉：CMU「冷扑大师」不完美信息博弈研究获奖

本文经机器之心（微信公众号：almosthuman2014）授权转载，禁止二次转载

选自arXiv

机器之心报道

距离 NIPS 2017 开幕还有半月左右，但相关奖项的信息已经开始流出。CMU 教授 Tuomas Sandholm 的个人主页显示，他和其博士生 Noam Brown 获得了 NIPS-17 最佳论文奖。经机器之心求证，获奖论文为《Safe and Nested Subgame Solving for Imperfect-Information Games》。本文将对这篇论文进行简要介绍。

Tuomas Sandholm 个人主页：http://www.cs.cmu.edu/~sandholm/

机器之心就最佳论文问题向 Tuomas Sandholm 本人进行求证，并得到了肯定的回复。

2017 年，最为人们关注的人机大战除了柯洁与 AlphaGo 的围棋比赛之外，就是 CMU 的德州扑克 Libratus 击败世界顶尖扑克选手了。

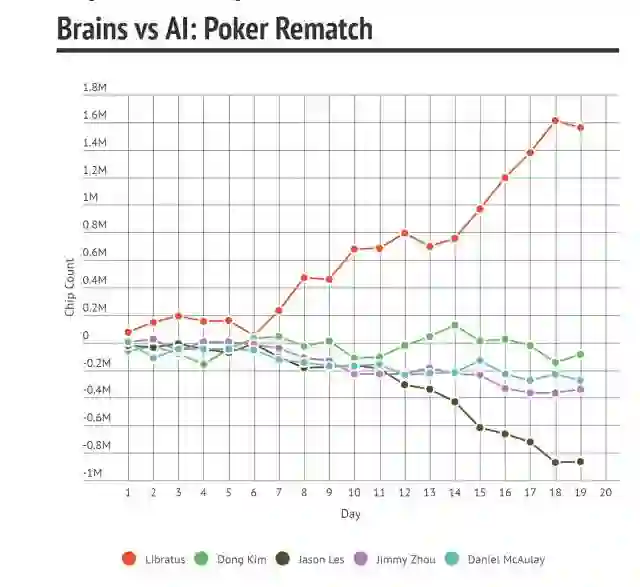
2017 年 1 月 30 日，在宾夕法尼亚州匹兹堡的 Rivers 赌场，卡耐基梅隆大学（CMU）开发的 Libratus 人工智能系统击败人类顶级职业玩家。此次比赛共持续 20 天，由 4 名人类职业玩家 Jason Les、Dong Kim、Daniel McAulay 和 Jimmy Chou 对战人工智能程序 Libratus，在为期 20 天的赛程里面对玩 12 万手，争夺 20 万美元的奖金。最终的结果是「比赛过程中，人类选手整体上从未领先过。」

据介绍，Liberatus 用了很多蛮力计算来发挥到最佳水平，此外还利用了博弈论。而 CMU NIPS 2017 的这篇获奖论文对其背后的技术做了详细的解读，以下是机器之心对此论文的介绍。

论文：Safe and Nested Subgame Solving for Imperfect-Information Games

论文链接：https://arxiv.org/abs/1705.02955

和完美信息博弈不同，不完美信息博弈不能通过将博弈分解为可独立求解的子博弈而求得占优策略。因此我们越来越多地使用计算密集的均衡判定技术，并且所有的决策必须将博弈的策略当做一个整体。由于不能通过精确的分解来解决不完美信息博弈，人们开始考虑近似解，或通过解决不相交的子博弈提升当前结果。这个过程被称为子博弈求解（subgame solving）。我们提出了一种无论在理论上还是在实践上都超越了之前方法的子博弈求解技术。我们还展示了如何对它们和以前的子博弈求解技术进行调整，以对超出初始行动提取（original action abstraction）的对手的行动做出应答；这远远超越了之前的顶尖方法，即行动转化（action translation）。最后，我们展示了当博弈沿着博弈树向下进行时，子博弈求解可能会重复进行，从而大大降低可利用性。我们应用这些技术开发了能在一对一无限注德州扑克单挑中打败顶尖人类选手的第一个 AI。

简介

不完美信息博弈模型的策略设置中存在隐藏的信息。这种模型有大量的应用，包括谈判、拍卖、网络安全以及人身安全。在这样的博弈中，通常的目标是寻找一个纳什均衡，即为每一个玩家分配一个组合策略，从而没有任何玩家能单方面转向另一个策略而提高自己的收益。

子博弈求解在完美信息博弈（比如象棋和西洋跳棋）中是一种标准的求解技术，其中博弈的每一部分都能独立求解。这在完美信息博弈中是可行的，因为博弈的确切状态是已知的，从而允许对博弈的余下过程中遗留的子博弈进行独立求解。例如，在象棋中，对后翼弃兵（一种象棋术语，下同）最佳响应不需要任何对西西里防御的最佳响应的知识。这种分解方法是 AI 能够在象棋和围棋中打败顶尖人类选手的关键所在。在西洋跳棋中，将博弈分解成较小的互相独立的子博弈的能力甚至能用于求解整个博弈。

相反的是，不完美信息博弈不能如完美信息博弈那样通过分解而进行求解，因为一个子博弈的最佳策略可能依赖于其它尚未得到的子博弈的策略和输出。虽然这是一个反直觉的想法，我们在第 2 节里对其作出了证明。

相比依赖于分解，过去求解不完美信息博弈的经典方法是将博弈当成一个整体来求解。例如，限注德州扑克单挑（一种相对简单的扑克游戏，有 1013 个决策点）不需要做分解就能得到基本的求解。然而，这种方法不能扩展到大型博弈中，比如无限注德州扑克单挑（不完美信息博弈求解的一个主要的基准问题）有 10,161 个决策点，甚至当允许分数下注的时候会达到无限个。在如此大型的博弈中计算策略的标准方法是首先生成一个博弈的抽象（abstraction）表征，这是博弈的简化版本，保留了原始博弈尽可能多的策略特征。例如，将一个连续的行动空间离散化。这个抽象的博弈可以求解，当在进行完整博弈的时候，通过将完整博弈中的状态映射到抽象博弈中的状态，就能应用这个解。例如，在将连续行动空间离散化的例子中，舍入最近邻的离散行动。在极端大型的博弈中，过于简单的抽象可能无法包含博弈的所有决策复杂性，而且其解可能在原始的博弈中距离纳什均衡非常远。

出于这一原因，当我们沿着博弈树向下选择策略时，试图提升策略就变的很自然了，并且剩余的子博弈变的更小，尽管这也许不会导致纳什均衡。例如，在游戏开始之时，我们可以在提取中包含游戏早期阶段的大量大小不同的赌注，但只为最后几轮保留少量大小不同的赌注。当我们来到游戏的最后几轮，我们可以在子博弈中计算一种新策略，其中有最后几轮的大量大小不同的赌注。尽管通过这种方式独立地分析子博弈也许不可能达到一个精确的均衡，但是当原始策略不是最优时，它也许有可能在这些子博弈中提升策略。

第 2 节中我们首次展示了一个直观示例，它证明了为什么不完美信息子博弈无法像完美信息博弈一样通过独立求解子博弈而得到均衡解。第 3 节定义了符号，并提供了下文使用的背景信息。第 4 节回顾了用于不完美信息博弈的子博弈求解的先前方法。接着第 5 节提出了一种新的子博弈求解方法，它同时具备先前最佳方法的理论保证和更优的实际表现。第 6 节中提出一种替代形式的子博弈求解技术，在模型假设中它对误差更鲁棒，这弱化了算法的理论有效性，但是显著提升了性能。同时这一节对那些想要实现和在本论文基础上进一步扩展的人很重要。第 7 节引入一种子博弈求解方法，它被嵌套为玩家的博弈树，相比于先前最优的方法行动转化，它大大提升了性能。最后，第 8 节通过实验展示了这些新的子博弈求解技术，相比于先前技术显著降低了可利用性。论文同时也展示了 2017 年人机大战的结果，其中使用论文所述技术的 Libratus 首次在一对一无限注德扑中击败了人类顶级玩家，实现了历史性突破。

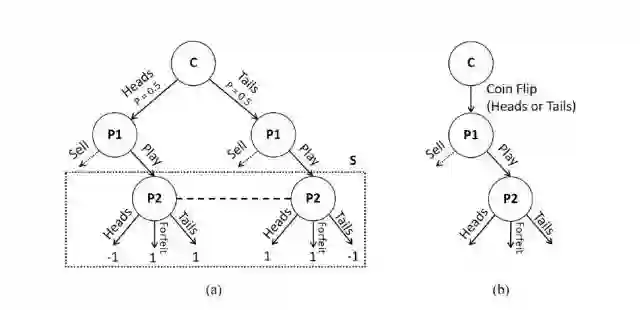
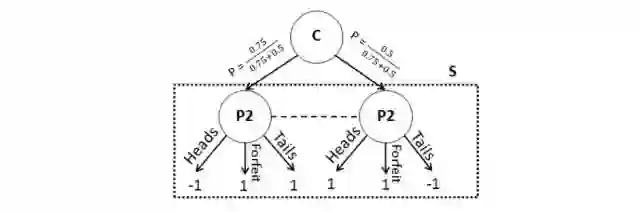
图 1：（a）掷硬币示例。C 表示一个可能性节点。S 是玩家 2（P2）的一个子博弈。两个 P2 节点之间虚线意味着 P2 无法区分它们。（b）掷硬币的公共博弈树。掷硬币的两个结果只被 P1 观察。

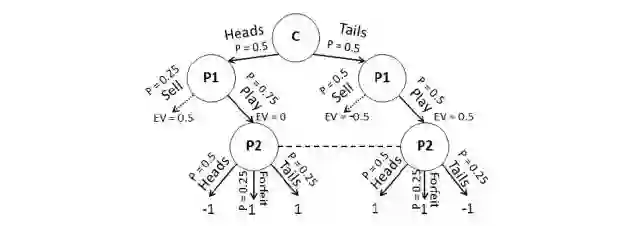
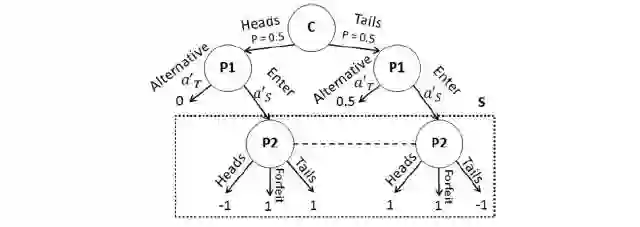
图 2：掷硬币游戏中提到的主干策略。Sell 操作导致子博弈未显示。所有操作的可能性都有显示。由于 P2 节点分享了信息集，该行动上每个节点的概率必须相同。图中还显示了每个 P1 行动最佳反事实返回值。

图 3：增强子博弈通过非安全掷硬币子博弈确定的 P2 策略。

图 4. 增强子博弈通过重新求解确定掷硬币子博弈确定的 P2 策略。

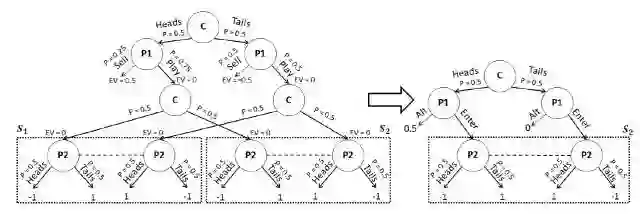
图 5. 左：两个子博弈的游戏。节点 C1 和 C2 是公共节点，其结果被 P1 和 P2 所见。右：其中一个子游戏的增强子游戏。如果只有一个子游戏被解，Head 上的替代回报最多为 1。但是，如果两者被独立解决，则 gift 必须在子游戏之间分裂，其和接近 1。例如，两个子游戏的替代回报可以都是 0.5。

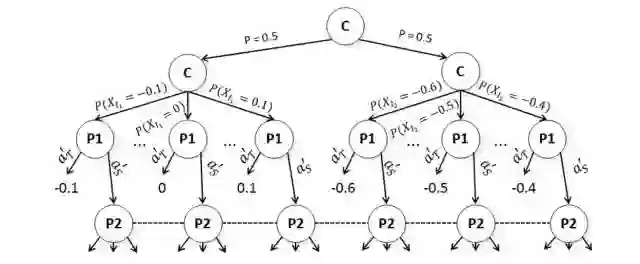
图 6:使用分布式可替代支付矩阵，增强子博弈从图 4 开始变化的可视化

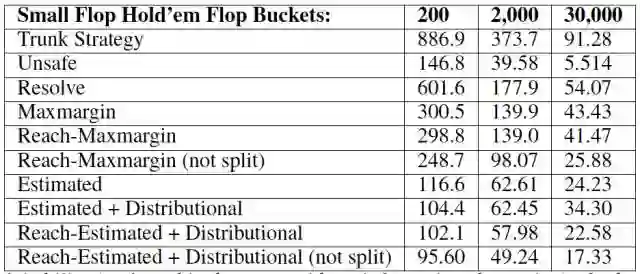
表 1:德州扑克前三张牌（flop) 小时的子博弈求解的 Exploitability 值（是在没有信息提取的博弈中评估的）

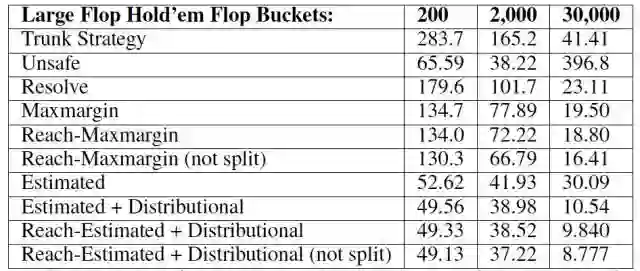
表 2:德州扑克开前三张牌（flop）大时的子博弈求解的 Exploitability 值（是在没有信息提取的博弈中评估的）

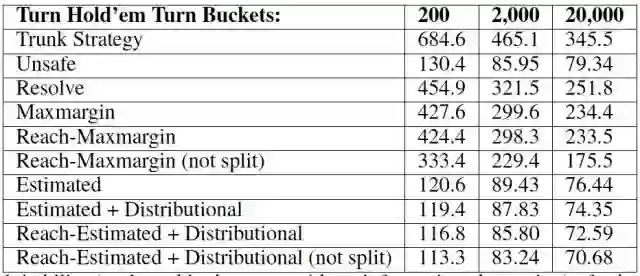
表 3:德州扑克掀第四张牌时子博弈求解的 Exploitability 得分（是在没有信息提取的博弈中评估的）

表 4：嵌套子博弈求解中各种子博弈求解技术的对比。pseudo-harmonic 行动转换的表现也有所体现。Exploitability 一栏是在大型行动提取中的评估得分，在此实验中没有信息提取。

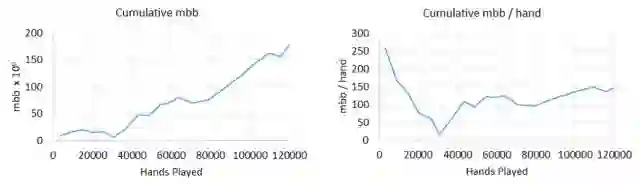
图 7:Libratus 在 2017 年 Brain vs. AI 大赛中的表现

结论

我们引入了一种用于不完美信息博弈的子博弈求解技术，相比之前的同类方法，它有着更强的理论保证和更好的实际表现。我们同时展示了安全与非安全子博弈求解技术的可利用性结果。我们同样为嵌套子博弈求解引入新方法，从而回应于相对反的 off-tree 行动，并证明相比于通常的行动转化，这将会显著提升性能。据我们所知，这是首次在大型游戏中实现子博弈求解技术的可利用性的测量。

最后，在一对一无限注德州扑克游戏上，我们的技术在与人类顶级玩家的对战中证明了其有效性，这是 AI 在不完美信息博弈中的一次主要基准挑战。在 2017 年的人机大战中，Libratus 取得里程碑式突破，成为在一对一无限注德扑上战胜人类顶级玩家的首个 AI。

在 12 月举行的 NIPS 2017 大会上，Tuomas Sandholm 等人还将提交该论文的更新版，敬请期待。 

点击「阅读原文」，参与 NIPS 2017 线上分享第二期。