【重磅】DeepMind发布Nature论文: 博弈网络让智能体成为游戏大咖

2018 年 1 月 17 日 专知专知内容组（编）

【导读】近日，DeepMind在《Nature Science》发布最新论文，研究将博弈论应用在multi-agent的游戏中，利用纳什均衡在自我对局中消除分歧，寻找最优平衡策略。将非对称游戏有效分解为两种独立的对称系统，从而用传统方法解决，并能推广到解决现实中的不对称问题，其官网上也发布了对这篇论文的详细解读。专知内容组编辑整理。

Game-theory insights into asymmetric multi-agent games

博弈论对非对称multi-agent游戏的启示

随着人工智能系统开始在现实世界中扮演越来越重要的角色，了解这些不同的系统是如何相互作用是很重要的。

在我们最近发表在《Nature》杂志（journal Scientific Reports）上的一篇论文中，我们使用了博弈论的一个分支来阐明这个问题。具体来说，我们研究了两种智能系统在非对称游戏情况下的行为和反应，其中包括Leduc扑克和各种各样的棋盘游戏，比如Scotland Yard。不对称游戏也会自然地模拟某些真实场景，比如买家和卖家在不同的动机下运作的自动拍卖。我们的研究结果让我们对这些情况有了新的认识，并揭示了一种分析这些情况的简单方法。虽然我们的兴趣在于如何将这个理论应用于多个人工智能系统的交互，但我们相信这些结果也可以用于经济学、进化生物学和经验博弈理论等领域。

这个方法被证明在数学上很简单，可以对非对称游戏进行快速而直接的分析。

博弈论是一个数学领域，用来分析决策者在竞争环境中所使用的策略。它可以适用于各种情况下的人类、动物和计算机分析，但在人工智能研究中通常用于多个系统的“multi-agent”环境，例如多个家庭机器人合作清洁房屋。传统上，multi-agent系统的演化动态使用简单的对称游戏进行分析（如经典的“囚徒困境Prisoner’s Dilemma”），每个玩家都可以使用同一组动作。虽然这些游戏对multi-agent系统如何工作可以提供一些有用的见解，并告诉我们如何使所有参与者达到理想的结果——即所谓的纳什均衡（Nash equilibrium）——但他们不能模拟所有情况。

我们的新技术使我们能够快速、轻松地识别用于更复杂不对称博弈中找到Nash equilibrium的策略——以每个参与者具有不同策略、目标和回报的博弈为特征。这些游戏以及我们用来理解它的新技术——可以用博弈论中常用的“性别之战Battle of the Sexes”的例子来说明。

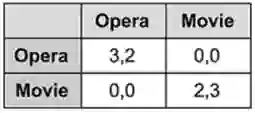
在这里，两个玩家不得不协调同一个晚上去听歌剧还是看电影。其中一位玩家对歌剧比较感兴趣，其中一位对电影比较感兴趣。这游戏是不对称的，因为虽然两个玩家都可以使用相同的选项，但根据玩家的喜好，每个玩家的相应奖励是不同的。为了维持友谊或平衡，玩家应该选择相同的活动（因此单独活动具有零回报）。

这个游戏有三个均衡的情况：

（i）两个玩家都决定去歌剧

（ii）两个都决定去看电影

（iii）最后的混合选项

其中每个玩家用五分之三的可能性来选择他们喜欢的选项。最后这种“不稳定”的情况可以用我们的方法，通过将不对称博弈简化或分解成对称博弈而迅速解决。类似的这些游戏本质上把每个玩家的奖励表作为一个独立的对称双人游戏，其平衡点与原来的非对称游戏相一致。

在下面的图中，通过两个简单的对应关系绘制了纳什均衡（Nash equilibrium），使我们能够快速确定不对称博弈中的最优策略（a）。反过来也使用不对称博弈来确定其对称的均衡。

红点代表纳什均衡。对于不对称的游戏(a)，很容易从两个对称副本(b)和(c)的图中推导出来，在所有图中，x轴对应于玩家1选择“歌剧”的概率，而y轴则对应于第二个玩家选择“歌剧”的概率。

这种方法也可以应用于其他游戏，包括Leduc扑克，这在本文中有详细的描述。在所有这些情况下，这种方法在数学上被证明是简单的，从而能够对非对称游戏进行快速和直接的分析，我们希望这能够帮助我们理解各种动态系统，包括multi-agent环境。

全文链接：

https://www.nature.com/articles/s41598-018-19194-4

这项工作由Karl Tuyls，Julien Perolat，Marc Lanctot，Georg Ostrovski，Rahul Savani，Joel Leibo，Toby Ord，Thore Graepel和Shane Legg完成。

原文链接：

https://deepmind.com/blog/game-theory-insights-asymmetric-multi-agent-games/

▌论文

论文地址：

https://www.nature.com/articles/s41598-018-19194-4

Symmetric Decomposition of Asymmetric Games

摘要：我们在两种不对称的游戏中引入了新的理论，允许对两种单一不对称游戏进行简洁的对称分解。具体地，我们通过构想和调查构成非对称博弈的收益表（A和B）作为两个独立的单一对称游戏，展示了一个不对称的bimatrix游戏(A，B)如何被分解成对称的副本。我们揭示了非对称的两种群（asymmetric two-population game）与对称的单一种群（symmetric single population）之间的一些令人惊讶的关系，由于分解的维度减少了，所以这有助于对原始的非对称博弈进行分析。主要的发现显示，如果（x，y）是非对称博弈（A，B）的纳什均衡，则这意味着y是由收益表A确定的对称博弈的纳什均衡，x是由收益表B确定的对称博弈的纳什均衡。我们通过检验几个典型例子中较简单游戏的演化动态，举例说明了这些关系是如何帮助识别和分析非对称博弈的纳什结构的（Nash structure）。

-END-

专 · 知

人工智能领域主题知识资料查看获取：【专知荟萃】人工智能领域26个主题知识资料全集（入门/进阶/论文/综述/视频/专家等）

同时欢迎各位用户进行专知投稿，详情请点击：

【诚邀】专知诚挚邀请各位专业者加入AI创作者计划！了解使用专知！

请PC登录www.zhuanzhi.ai或者点击阅读原文，注册登录专知，获取更多AI知识资料！