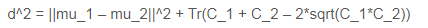学习GAN模型量化评价,先从掌握FID开始吧
选自machinelearningmastery
作者:Jason Brownlee
机器之心编译
编译:高璇,Geek AI
要说谁是当下最火的生成模型,GAN 当之无愧!然而,模式坍塌、训练不稳定等问题严重制约着 GAN 家族的发展。为了提图像质量、样本多样性的角度量化评价 GAN 模型的性能,研究者们提出了一系列度量指标,其中 FID 就是近年来备受关注的明星技术,本文将详细介绍如何在 python 环境下实现 Frechet Inception 距离(FID)。
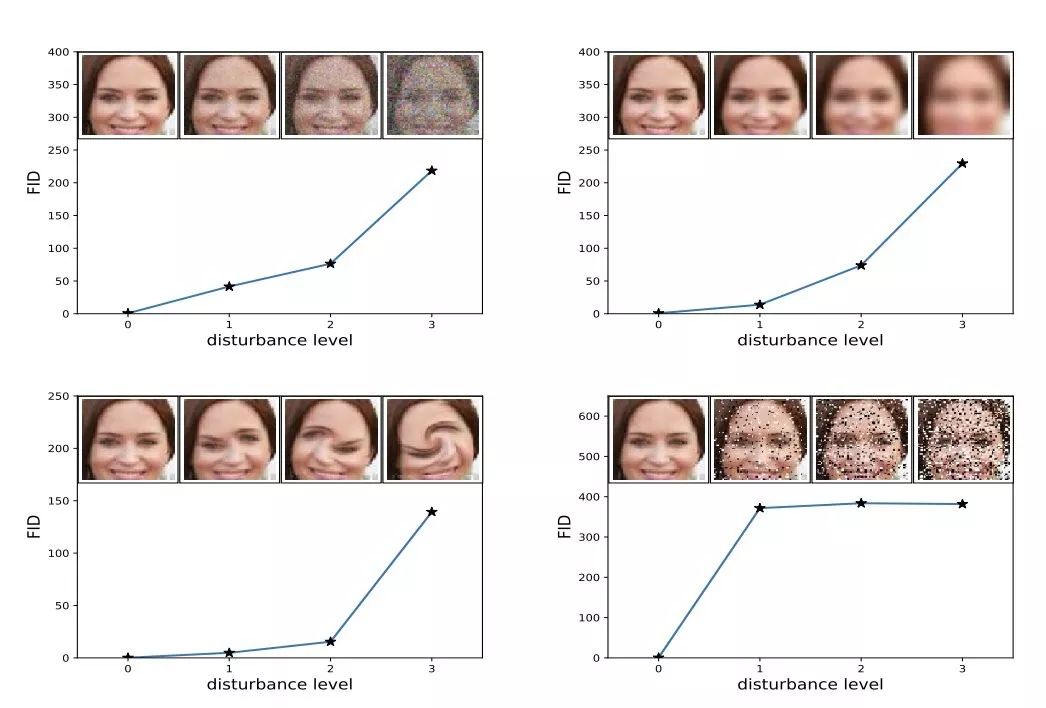
Frechet Inception 距离得分(Frechet Inception Distance score,FID)是计算真实图像和生成图像的特征向量之间距离的一种度量。
FID 综合表征了相同的域中真实图像和生成图像的 Inception 特征向量之间的距离。
如何计算 FID 分数并在 NumPy 环境下实现 FID。
如何使用 Keras 深度学习库实现 FID 分数并使用真实图像进行计算。
何为 FID?
如何计算 FID?
如何通过 NumPy 实现 FID?
如何通过 Keras 实现 FID?
如何计算真实图像的 FID?
为了评估 GAN 在图像生成任务中的性能,我们引入了「Frechet Inception Distance」(FID),它能比 Inception 分数更好地计算生成图像与真实图像的相似性。——「GANs Trained by a Two Time-Scale Update Rule Converge to a Local Nash Equilibrium」(https://arxiv.org/abs/1706.08500), 2017.
Inception 分数的缺点是没有使用现实世界样本的统计量,并将其与合成样本的统计量进行比较。——「GANs Trained by a Two Time-Scale Update Rule Converge to a Local Nash Equilibrium 」(https://arxiv.org/abs/1706.08500), 2017.
两个高斯分布(合成图像和真实图像)的差异由 Frechet 距离(又称 Wasserstein-2 距离)测量。 ——「GANs Trained by a Two Time-Scale Update Rule Converge to a Local Nash Equilibrium」(https://arxiv.org/abs/1706.08500), 2017.
def calculate_fid(act1, act2):
# calculate mean and covariance statistics
mu1, sigma1 = act1.mean(axis=0), cov(act1, rowvar=False)
mu2, sigma2 = act2.mean(axis=0), cov(act2, rowvar=False)
# calculate sum squared difference between means
ssdiff = numpy.sum((mu1 - mu2)*2.0)
# calculate sqrt of product between cov
covmean = sqrtm(sigma1.dot(sigma2))
# check and correct imaginary numbers from sqrt
if iscomplexobj(covmean):
covmean = covmean.real
# calculate score
fid = ssdiff + trace(sigma1 + sigma2 - 2.0 covmean)
return fid
act1 = random(102048)
act1 = act1.reshape((10,2048))
act2 = random(102048)
act2 = act2.reshape((10,2048))
fid = calculate_fid(act1, act1)
print('FID (same): %.3f' % fid)
fid = calculate_fid(act1, act2)
print('FID (different): %.3f' % fid)
import numpy
from numpy import cov
from numpy import trace
from numpy import iscomplexobj
from numpy.random import random
from scipy.linalg import sqrtm
def calculate_fid(act1, act2):
# calculate mean and covariance statistics
mu1, sigma1 = act1.mean(axis=0), cov(act1, rowvar=False)
mu2, sigma2 = act2.mean(axis=0), cov(act2, rowvar=False)
# calculate sum squared difference between means
ssdiff = numpy.sum((mu1 - mu2)*2.0)
# calculate sqrt of product between cov
covmean = sqrtm(sigma1.dot(sigma2))
# check and correct imaginary numbers from sqrt
if iscomplexobj(covmean):
covmean = covmean.real
# calculate score
fid = ssdiff + trace(sigma1 + sigma2 - 2.0 covmean)
return fid
act1 = random(102048)
act1 = act1.reshape((10,2048))
act2 = random(102048)
act2 = act2.reshape((10,2048))
fid = calculate_fid(act1, act1)
print('FID (same): %.3f' % fid)
fid = calculate_fid(act1, act2)
print('FID (different): %.3f' % fid)
FID (same): -0.000
FID (different): 358.927
登录查看更多
相关内容
Arxiv
4+阅读 · 2020年3月5日
Arxiv
15+阅读 · 2019年1月15日
Arxiv
15+阅读 · 2018年5月24日