图机器学习 2.1 Properties of Networks, Random Graph

图网络的基础知识还是蛮深的，笔者听着觉得耗很多脑细胞。代码块里大部分是笔者个人理解，希望大家多指导和讨论～

networks的性质--怎么度量一个network？

（1）度的分布（degree distribution):

首先什么是度（degree）：根据邻近矩阵的信息，对每一个节点来计算其度（行和）

形象的理解：数一数每一个节点都有几条连接线（也就是这个节点的度）

img

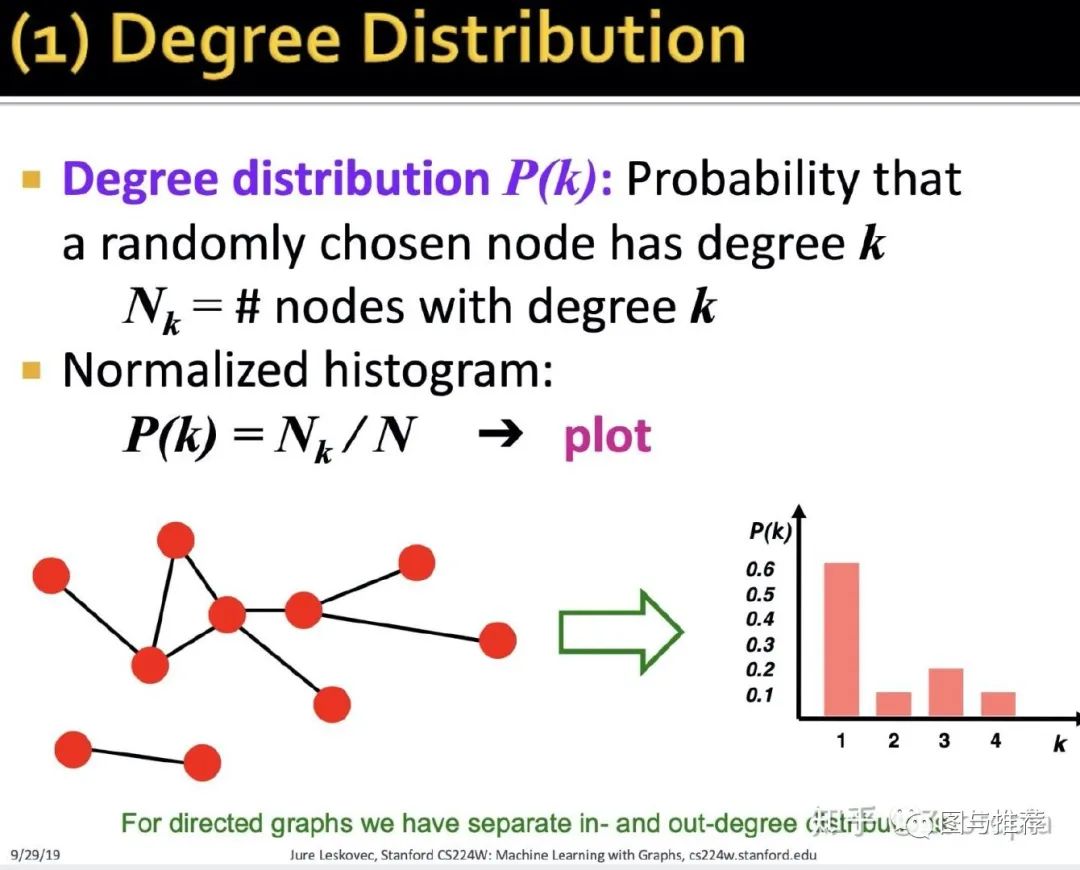
那度分布P(k)表示的是随机选择一个具有度为k的节点的概率

N（k）表示的是具有度为k的节点个数

有了这个N_k之后，对其进行归一化（也就是N（k)/总节点数）利用直方图画图

这样的方式就能从概率分布的角度直观的看到节点度的分布情况，例如从上图中我们可以观察到（微博用户，其中
1用户的关注+粉丝数量是比较大的，或者说用户1的活跃度是比较高的）

（2）图中的路径paths in a graph

也就是两两相邻节点进行连接后的路径---和我们常说的连通路径很类似

img

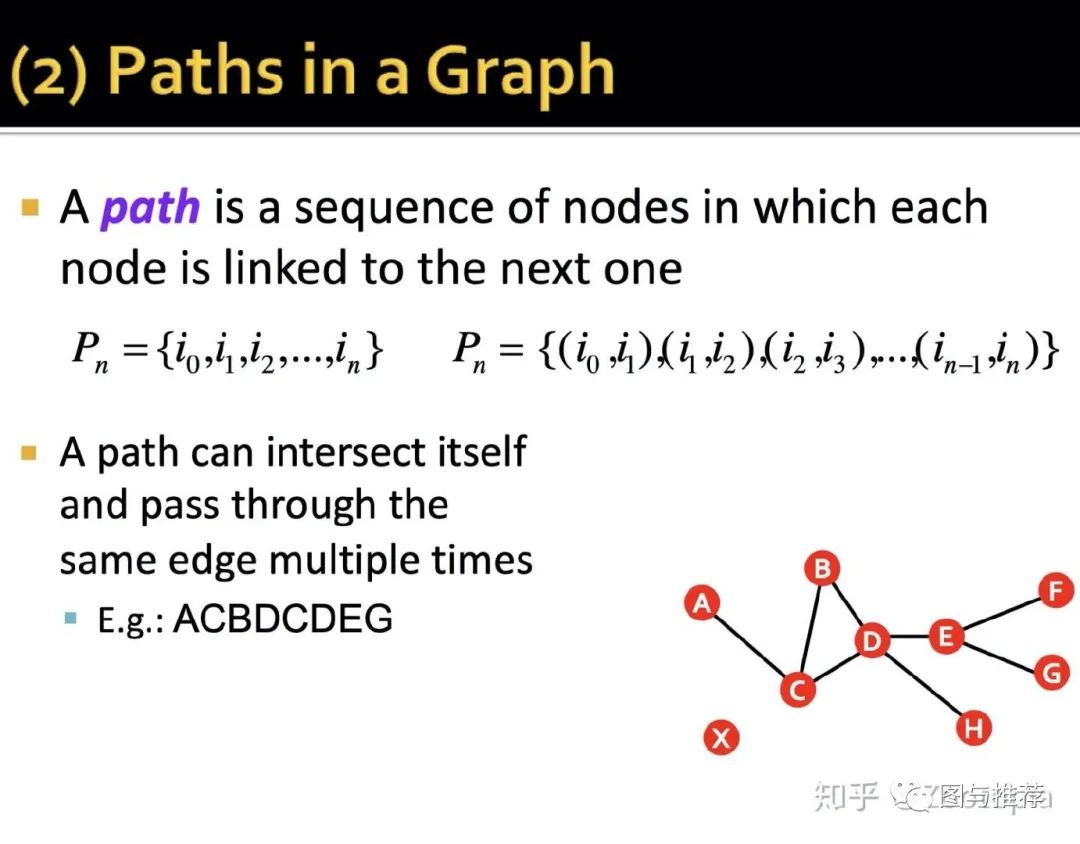
（3）图中的距离 distance in a graph

回顾我们数学基础课中定义的一个点到一个平面的距离：最短的路径

• 无向图中

图中的距离也可以约等于最短的路径，比如图中点B到D的距离（如果我们假设每两相邻节点之间连线数值为1）是2，那么点A到x则是无穷（因为没有路径）

• 有向图中（距离不满足对称性）因为在有向图中我们 要跟着箭头走

所以图中的B到C的距离是1，而节点C到节点B的距离则是2（C到A到B）

img

（4）聚类系数 clustering coefficient（针对无向图）

这个系数的提出是基于思考这样一个问题：节点i的neighbors都是如何连接的？

比如微信上，我作为节点i，我想看看我的朋友圈（neighbor)互相之间了解、互动有多少

img

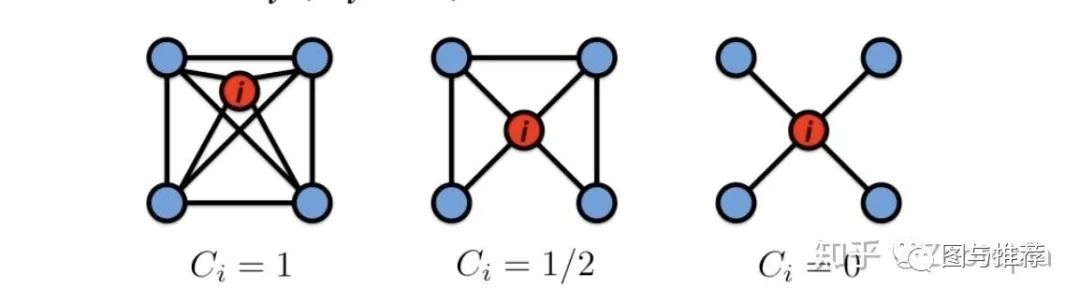
我是节点i，case 1:我的朋友们互相是know each other，那么系数C_i=1
         case 2:我的朋友们一部分相互认识，一部分毫无联系
         case 3:朋友们只和我认识，他们互不认识，这时候系数是0

注意：clustering coefficient是对每一个节点都设置的，计算公式是

img

下面将这些度量性质用于真实networks

思考问题：这些people是怎么联系each other？

img

img

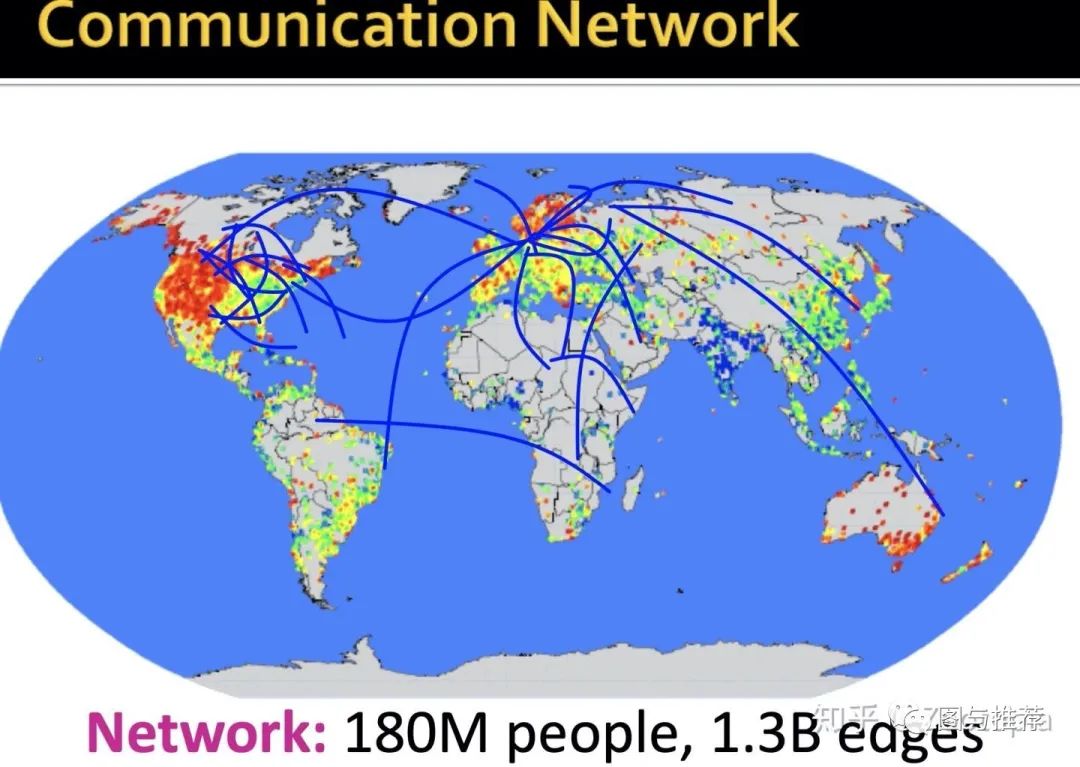
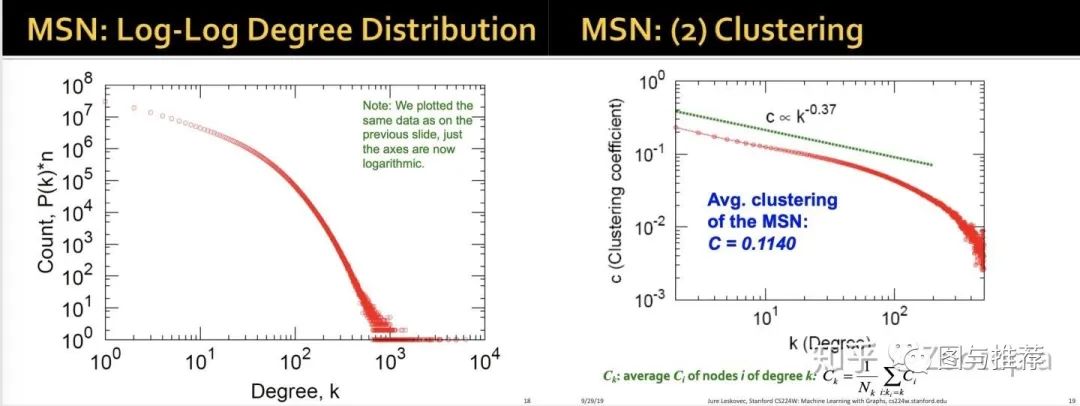
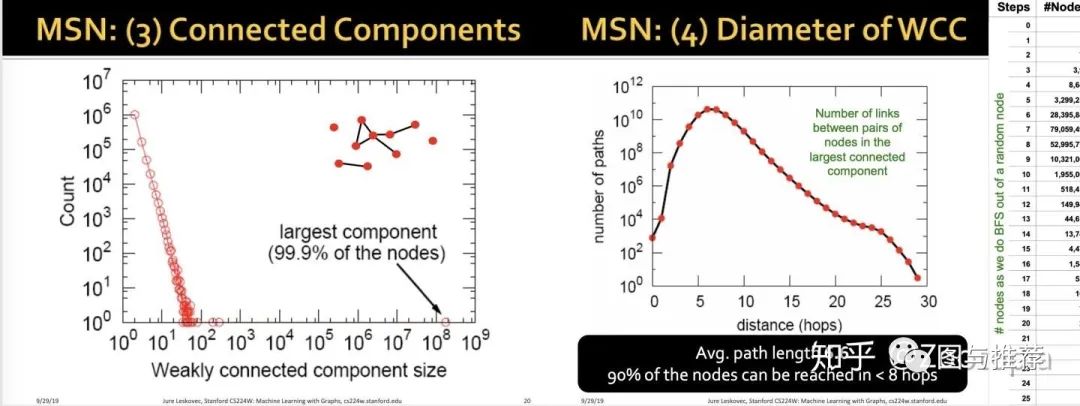
我们从diameter这个图可以看到，基本大部分人互相之间联系在“5”左右

平均路径长度是6.6，这和社会学中常说的每两个人之间只需要7个人即可相互
联系吻合

我们根据上面定义的图的一些属性得到的数据总结如下：

img

从这些数据中我们可以学到什么？先看另一个例子

img

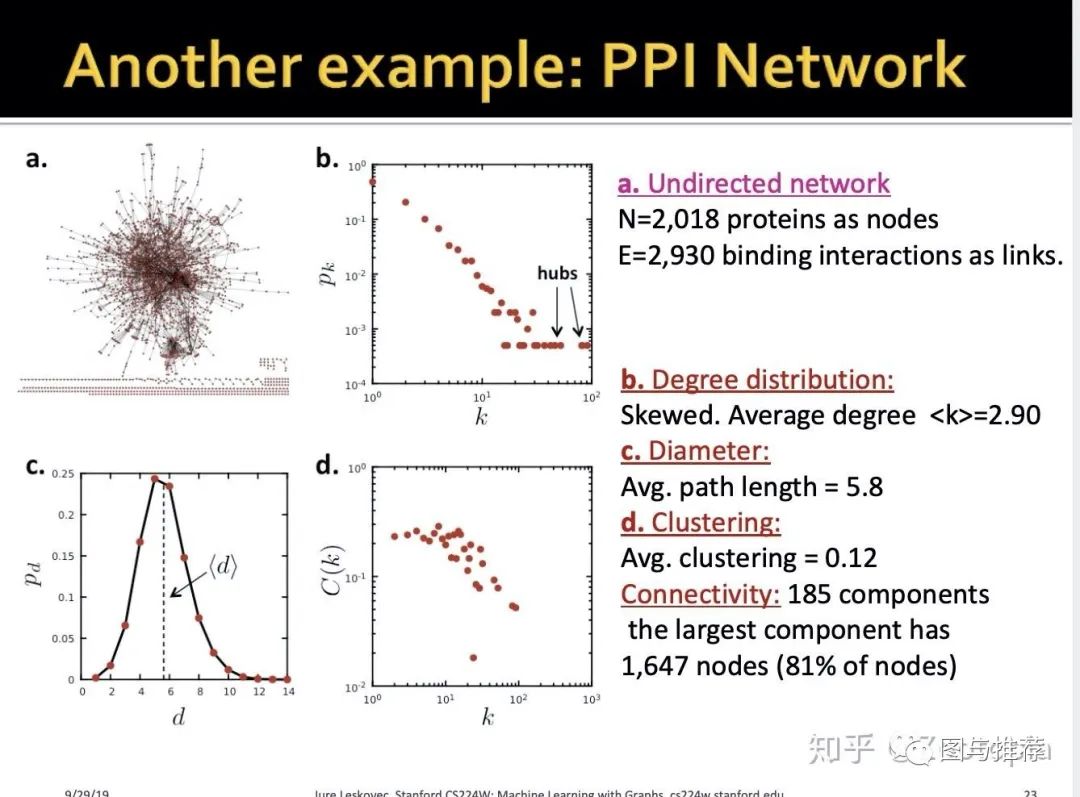
根据这个例子我们再次计算上面的那些属性：我们发现这些属性的数值和上一个例子是较为接近的

既然如此，那么根据具体的例子得到的属性，我们可以考虑其共性，建立我们需要的模型

所以下面我们需要考虑的就是一般的图模型的性质

random graph model

前面介绍了用来衡量一个图模型的几个主要属性，并且应用于实际中：msn人际关系图和PPI网络之后发现一些属性的值很接近

特殊->一般->建立模型

那么现在考虑一般情况下的模型：考虑最简单的图模型

【注意这里考虑的是无向图】我们用G_{np}来表示具有n个节点且每个边(u,v)都是服从概率p的独立同分布的无向图

img

【注意】n和p不能唯一决定图模型！

也就是说图其实是随机过程的一个结果，下图是给定n,p值的一个例子

img

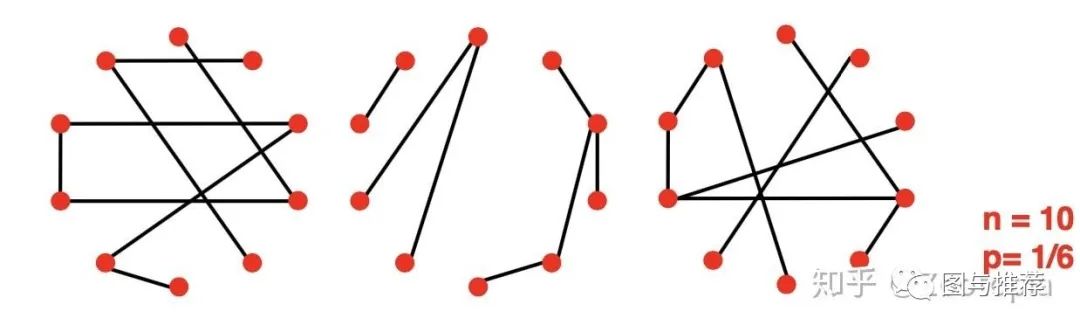
那么现在对于这么general的一个图，我们来看看前面提到的那些属性的值是多少

（1）度分布（degree distribution)

img

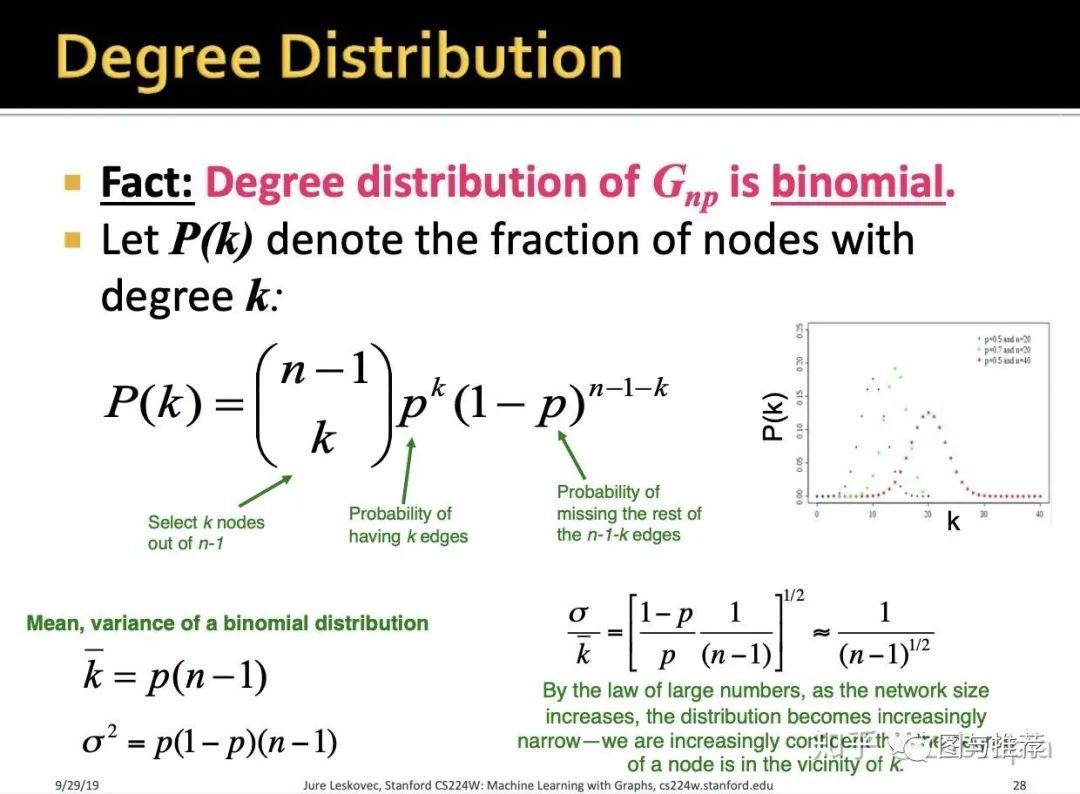
• P(k)：选定了一个节点，于是图中剩下n-1个节点，从剩下的节点中选取k个节点乘以这k个节点有k个边（也就是度为k）的概率
• 有了度分布，可以发现其是 二项式的
• 既然是二项式的我们就能得到其期望和方差

img

方差和期望的比值说明：当网络规模逐渐变大，平均值会越来越集中

对应了大数定理

img

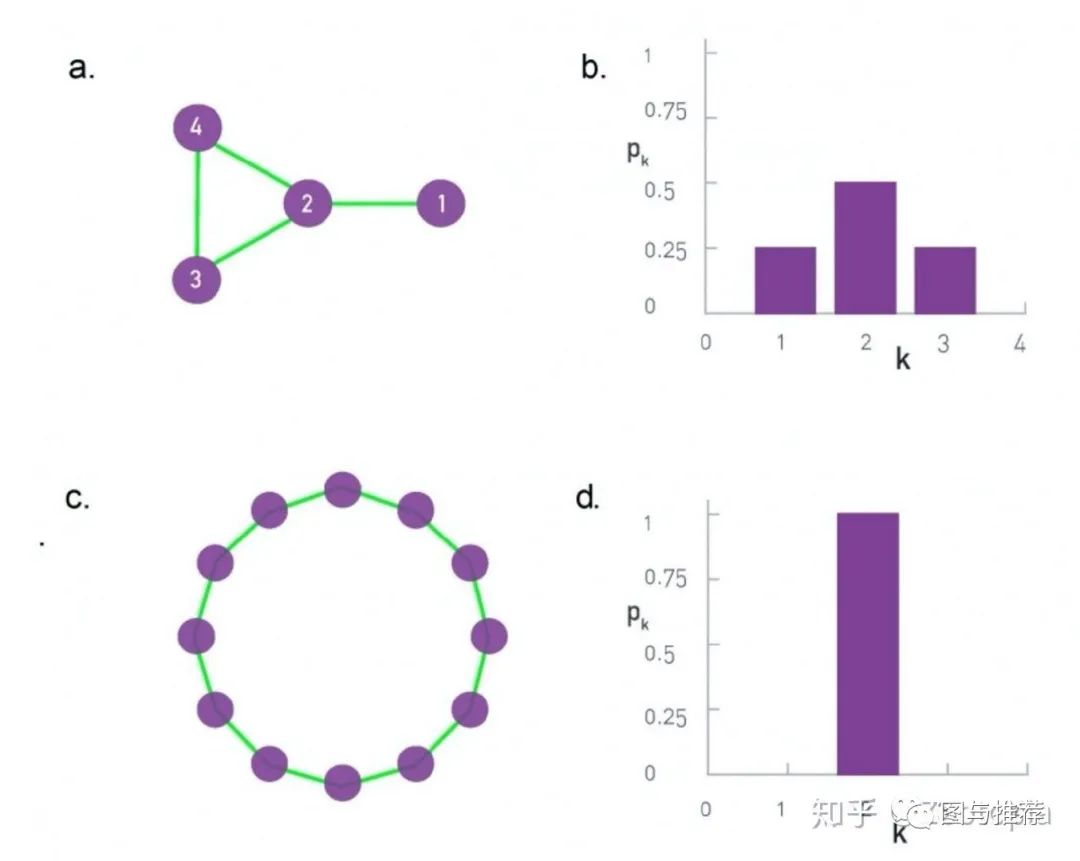
补充上一节的一个内容：注意到度的直方图有利于我们判断图的结构

（2）聚合系数

img

这里的计算比较显然，但是注意到E[Ci]可以发现当期望是一个固定值时，随着图规模越来越大，随机图的聚合系数会趋近于0。

【下面的学习部分，需要记住随机图的聚合系数是p】

讨论完了度分布和聚合系数，下面来看随机图的路径长度，这里通过“扩展(expansion）“来衡量

（3）expansion

什么是扩展数？

img

简单理解为：任取图中节点的一个子集，相对应的从子集中离开的（也就是和这些节点相关的）最小节点数目

或者还可以理解为：为了让图中一些节点不具备连接性，需要cut掉图中至少多少条边？

（answer：需要至少cut掉alpha Num(节点）条edges）

扩展数alpha也是一个用来衡量鲁棒性的一个度量

（4）largest connected component（最大连接元）

什么是最大连接元？我们看下面这个图就一目了然

图中标红的部分就是最大连接元：连接最多节点的部分

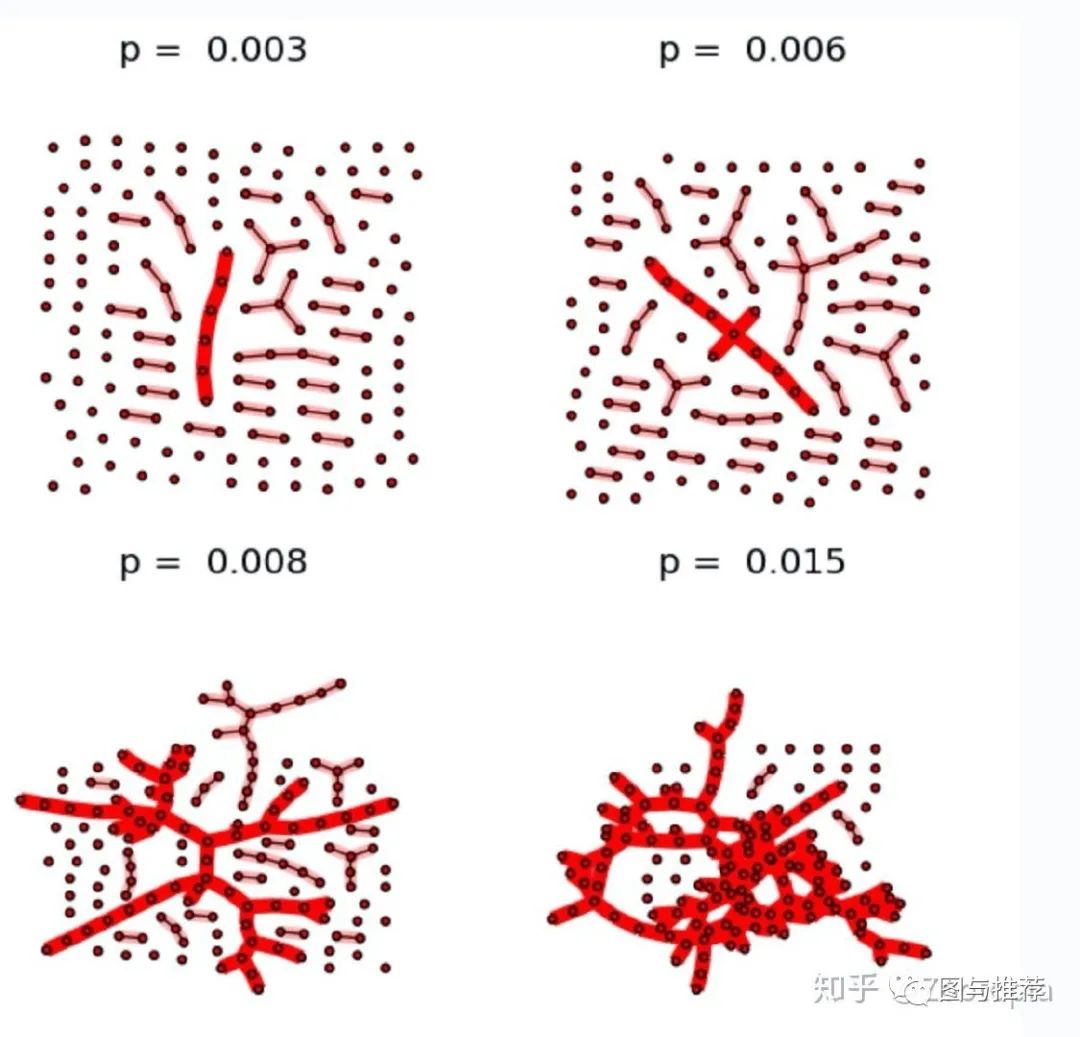
最大连接元的用途/意义：展示随机图的“进化”过程

当聚合系数=0的时候：也就是没有edge，这时候是一个空图

当聚合系数=1度时候：就是一个“全连接”的图

那么当聚合系数从0变化到1的过程中发生了什么变化？【当平均度=1的时候，因为k=p(n-1),此时聚合系数c=p=1/（n-1），出现了一个大连接元，以此类推】

img

学习完了随机图中的四个重要属性，下面来看随机图的应用性如何，看看和MSN数据的对比

img

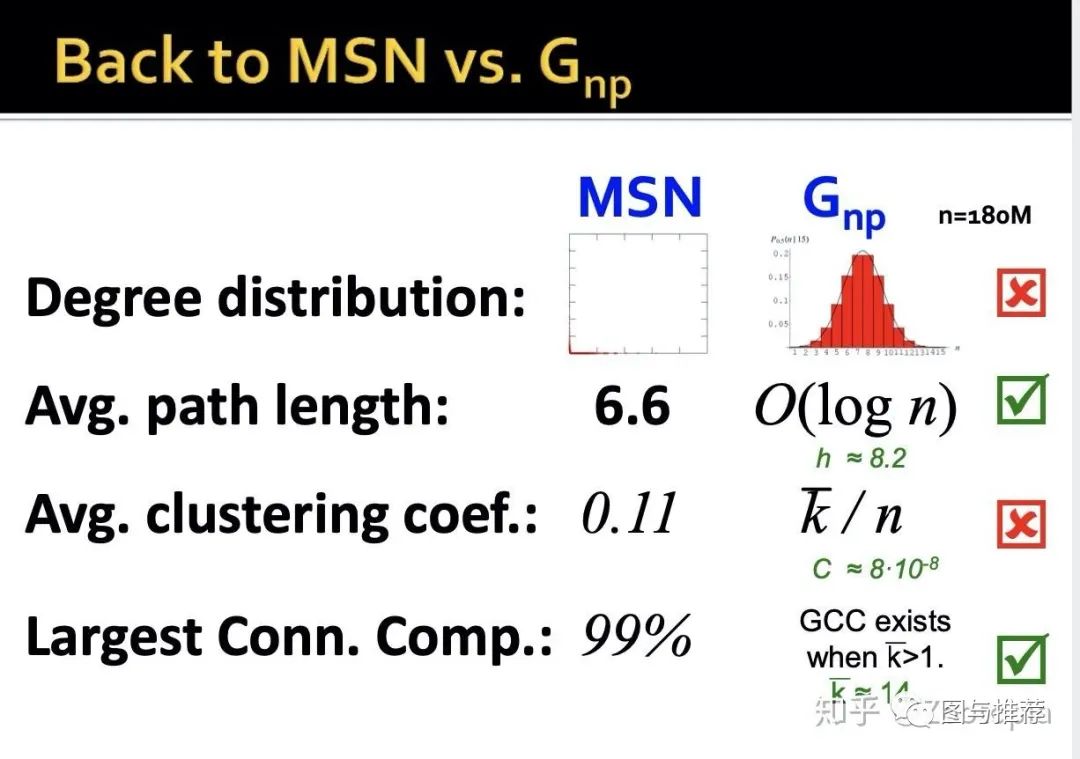
• 之前说过度分布的直方图有利于判断图的结构，MSN和随机图的直方图差距还是很大的；
• 平均路径：MSN和随机图的数据差不多
• 平均聚合系数：差距很大，随机图的非常小
• 最大连接元：很接近

综上来看，随机图的实际应用性如何？----不好！

img

从上面的属性比较可以看出：实际上的网络并不是随机的。

那么问题来了，既然如此又为什么要学习随机图呢？因为这是最简单也是最有效的学习和评估网络的方法！

随机性包罗万象，我们可以根据实际网络的特性来修改随机图来适应实际网络的需要

那么，如何让随机图实际应用性变强呢？

未完待续......