会员服务 ·

F-Principle：初探理解深度学习不能做什么

2019 年 1 月 31 日 PaperWeekly

作者丨许志钦、张耀宇

学校丨纽约大学阿布扎比分校博士后、纽约大学库朗研究所访问学者

研究方向丨计算神经科学、深度学习理论

近些年来，随着深度学习在众多实际应用中取得成功，在越来越多的科学领域内，研究人员开始尝试利用深度学习来解决各自领域的传统难题。和深度学习已获得成功的问题（比如图像分类）相比，许多科学领域内的问题往往有完全不同的特性。

因此，理解深度学习的适用性，即其能做什么尤其是不能做什么，是一个极为重要的问题。比如设计算法的时候，它可以帮助我们考虑是完全用深度学习来代替传统算法，还是仅在这个问题中的某些步骤用深度学习。

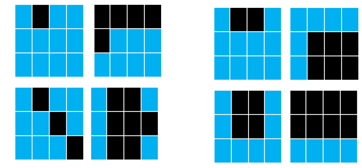
为了探讨这个问题，我们首先来看下面这个例子。在下面两组图中，左组中的每张图和右组有什么差别呢？

答案是左组的每张图中黑块数都是奇数，而右组都是偶数。这种按奇偶区分的函数数学上叫做 parity function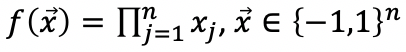：。其函数值由“-1”的个数决定，如果为偶数，结果为 1，否则为 -1。

对于该函数，如果取所有可能映射的一个子集进行训练，深度神经网络能够很好地拟合训练数据，但对那些未见过的测试数据，深度学习几乎没有预测（泛化）能力。而对于人来说，只要能从训练数据集中学到数“-1”个数这个规则，就很容易对未见过的数据进行准确分类。

对于很多问题，如图像识别，深度学习通常能取得较好的效果（泛化能力）。为了叙述方便，我们将这些深度学习能处理好的问题称为第一类问题，同时将深度学习处理不好（难以泛化）的问题称为第二类问题。

那么这两类问题有什么本质差别呢？深度学习模型为什么对这两类问题有截然相反的效果？

目前为止，大部分实验研究和理论研究集中于研究为什么深度学习能取得好的效果（泛化能力）。少部分的研究开始关注哪些问题深度学习难以处理。

在我们的研究中，我们希望能找到一个统一的机制，可以同时解释深度学习在两类问题中不同的效果。我们发现的机制可以用一句话概括：深度学习倾向于优先使用低频来拟合目标函数。我们将这个机制称为 F-Principle（频率原则）。

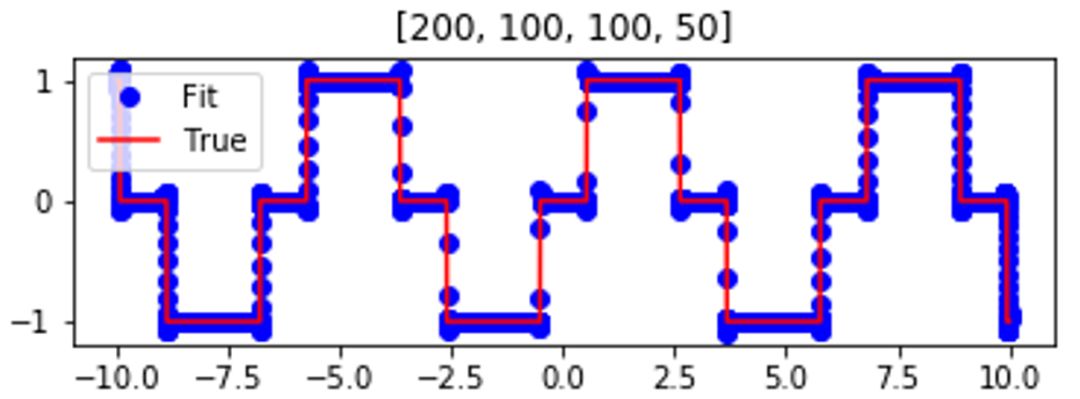
我们先用一个简单的例子来理解 F-Principle。用一个深度神经网络（DNN）去拟合如下的红色实线函数。训练完后，该曲线能被深度网络（蓝色点）很好地拟合。

我们感兴趣的是 DNN 的训练过程。如下图动画所示（红色为目标函数的 FT（傅里叶变换），蓝色为网络输出的 FT，每一帧表示一个训练步，横坐标是频率，纵坐标是振幅），我们发现，在训练过程中，DNN 表示的函数的演化在频域空间有一个清晰的规律，即频率从低到高依次收敛。

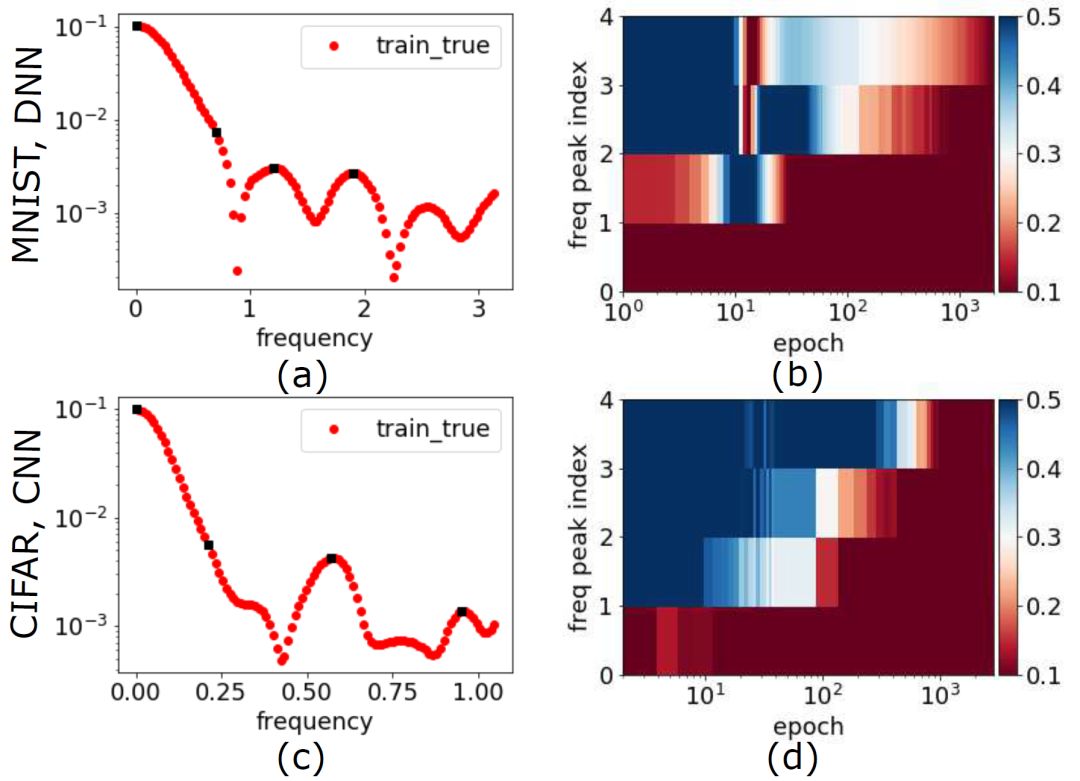
对于真实数据，如 MNIST 和 CIFAR10，对于不同的网络结构，如全连接和卷积神经网络（CNN），对于不同的激活函数，如 tanh 和 ReLU，我们都可以观察到 F-Principle（如下图所示）。

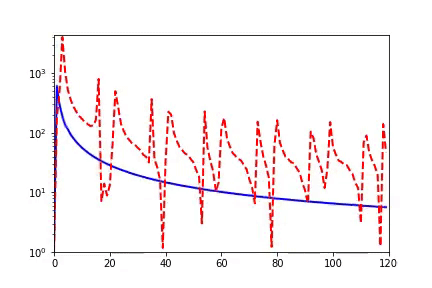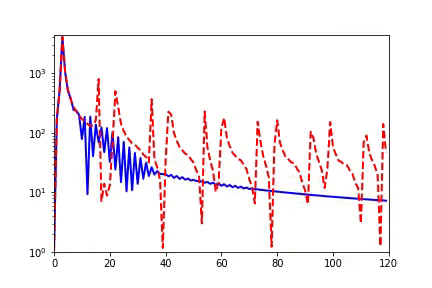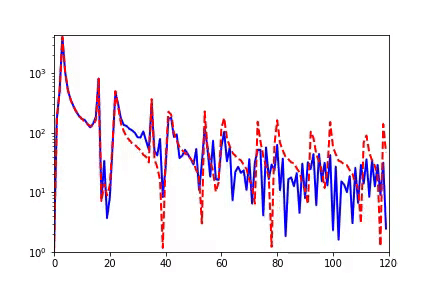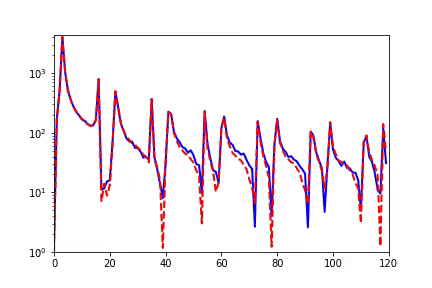
▲ 左边：数据集/DNN的Fourier变换在一个特定高维频率方向的变化曲线，右图：左图中黑色频率点处的相对误差与训练步数的关系，红色表示相对误差小。第一行是MNIST数据集的结果，使用全连接tanh网络。第二行是CIFAR10数据集的结果，使用ReLU-CNN网络。

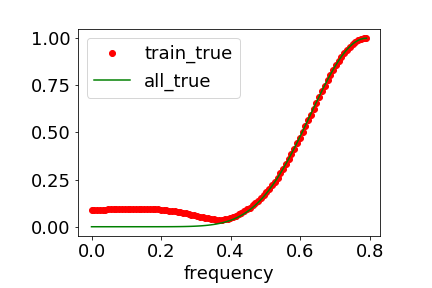
接下来，我们可以用 F-Principle 来理解为什么 DNN 在上述两类问题的处理中有巨大的差异。从频谱的角度，我们发现 MNIST 和 CIFAR10 数据集都有低频占优的特性。实验结果显示，全数据集（包含训练集和测试集）在频域空间与测试数据集在低频部分吻合地很好，如下图展示 MNIST 的情况。

parity 函数则不同，它是高频占优的。

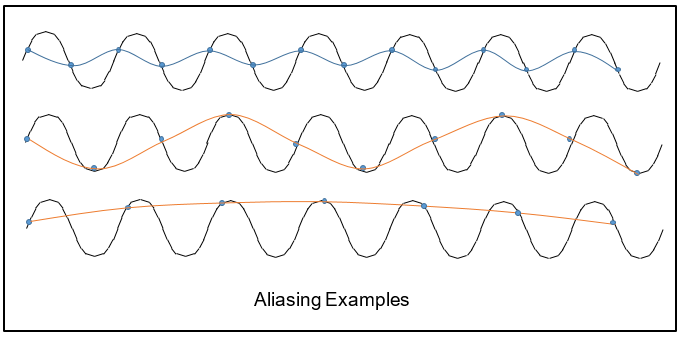
由于 aliasing 效应，相比真实的频谱，训练集的频谱在低频处有显著的虚假成分（见上图）。下图展示了一个 aliasing 的例子。

因此，对于我们举的例子，这两类问题在 Fourier 空间可以看到本质的差别。前者低频占优，后者高频占优。在训练过程中，基于 F-Principle 低频优先的机制，DNN 会倾向于用一个低频成分较多的函数去拟合训练数据。

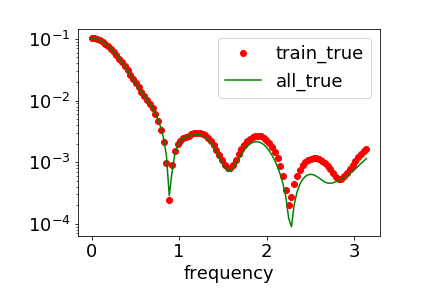
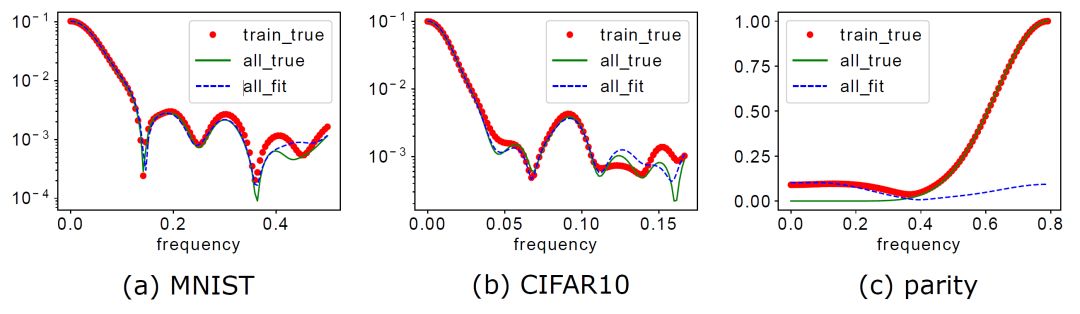
对于 MNIST 和 CIFAR10，一方面由于高频成分较小，aliasing 带来的虚假低频微不足道，另一方面由于 DNN 训练中低频优先的倾向与目标函数本身的低频占优的特性相一致，所以 DNN 能准确抓取目标函数的关键成分（下图蓝色为 DNN 学习到的函数在全数据集上的傅里叶变换在一个特定高维频率方向的曲线），从而拥有良好的泛化能力。

而对于 parity 函数，由于高频成分极为显著，aliasing 带来的虚假低频很严重，同时 F-principle 低频优先的倾向与目标函数本身高频占优的特性不匹配，所以 DNN 最终输出函数相比于目标函数低频显著偏大而高频显著偏小。显然，这种显著的差异会导致较差的泛化能力。

▲ 红色：训练数据集的傅里叶变换；绿色：全数据集的傅里叶变换；蓝色：网络输出在全数据集输入点的傅里叶变换

我们利用 F-Principle 对深度学习能做什么与不能做什么做了初步的探索，理解了具有低频优先特性的深度学习对于具有不同频谱特性的问题的适用性。如果目标函数具有低频占优的特性，那么深度学习比较容易取很好的效果，反之则不然。

进一步，我们可以利用深度学习这一特性更好地处理具体问题中的低频成分。比如传统算法（如 Jacobi 迭代）在解 Poisson 方程时，一般低频收敛慢，而高频收敛快。我们将在下一篇文章中介绍如何利用 F-Principle 机制设计基于 DNN 的 Poisson 方程求解方法。

参考文献

Xu, Zhi-Qin John, Zhang, Yaoyu, Luo, Tao, Xiao, Yanyang & Ma, Zheng (2019), ‘Frequency principle: Fourier analysis sheds light on deep neural networks’, arXiv preprint arXiv:1901.06523 .