数据结构与算法——图论基础与图存储结构
来自:五分钟学算法(微信号:CXYxiaowu)
1 前言
由于后续更新「面试专场」的好几篇文章都涉及到 图 这种数据结构,因此打算先普及一下 图 的相关理论支持,如果后面的相关内容有些点不太容易理解,可以查阅此篇文章。本文不建议一口气阅读完毕,可以先浏览一遍,在后续有需要的时候进行查阅即可。
2 图
图是数据结构中重要内容。相比于线性表与树,图的结构更为复杂。在线性表的存储结构中,数据直接按照前驱后继的线性组织形式排列。在树的结构中,数据节点以层的方式排列,节点与节点之间是一种层次关系。但是,在图的结构中数据之间可以有任意关系,这就使得图的数据结构相对复杂。
2.1 定义
定义:图(Graph)是由顶点的有穷非空集合和顶点之间边的集合组成,通常表示为:G(V,E),其中,G表示一个图,V 是图 G 中顶点的集合,E 是图 G 中边的集合。
例如:图 2.1 所示图

在图 2.1 中,共有 V0,V1,V2,V3 这 4 个顶点,4 个顶点之间共有 5 条边。
注:
当线性表没有数据节点时,线性表为空表。
树中没有节点时,树为空树。
但是,在图中不允许没有顶点,但是可以没有边。
2.2 无向边
无向边:若顶点 x 和 y 之间的边没有方向,则称该边为无向边(x,y),(x,y) 与 (y,x) 意义相同,表示 x 和 y 之间有连接。
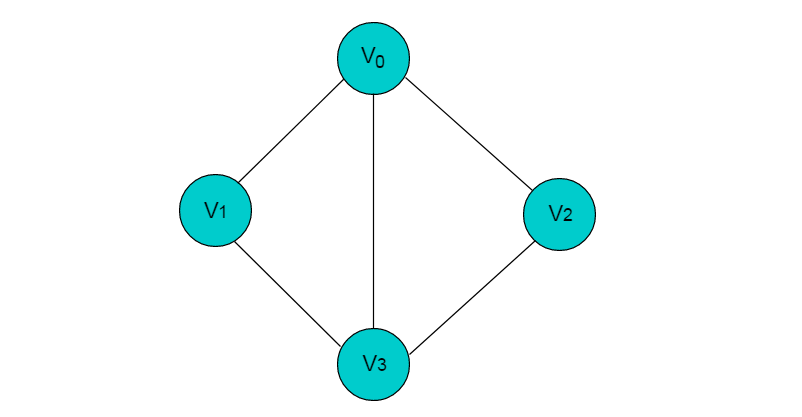
图 2.2 所示图中的边均为无向边。
2.3 有向边
有向边:若顶点 x 和 y 之间的边有方向,则称该边为有向边
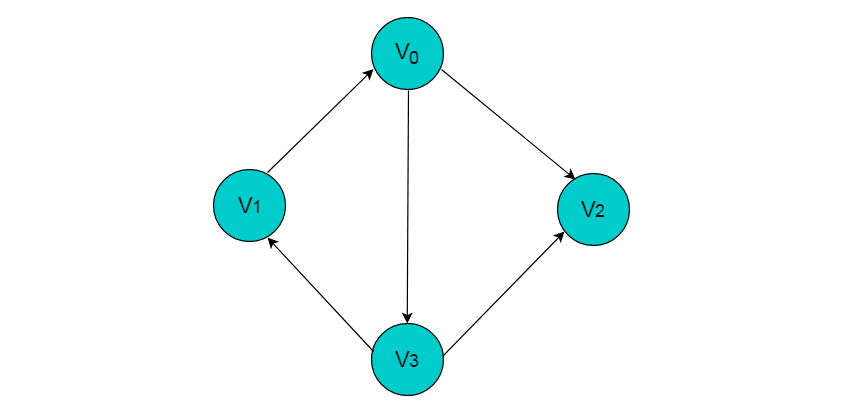
图2.3所示图中的边为有向边。
2.4 无向图
无向图:若图中任意两个顶点之间的边均是无向边,则称该图为无向图。
图2.2所示图为无向图。
2.5 有向图
有向图:若图中任意两个顶点之间的边均是有向边,则称该图为有向图。
图2.3所示的图为有向图。
2.6 顶点与顶点的度

顶点的度:
顶点 V 的度是和 V 相关联的边的数目,记为TD(V)。
图 2.6 所示图中,V0 顶点的度为 3 。
入度:
以顶点v为头的边的数目,记为ID(V)。
图2.6所示图中,V0的入度为1。
出度:
以顶点 v 为尾的边的数目,记为 OD(V)。
图2.6所示图中,V0的出度为2。
顶点的度 = 入度 + 出度。
即 TD(V) = ID(V) + OD(V)。
2.7 邻接
邻接是两个顶点之间的一种关系。如果图包含(u,v),则称顶点 v 与顶点 u 邻接。在无向图中,这也暗示了顶点 u 也与顶点 v 邻接。换句话说,在无向图中邻接关系是对称的。
2.8 路径
路径:在图中,依次遍历顶点序列之间的边所形成的轨迹。
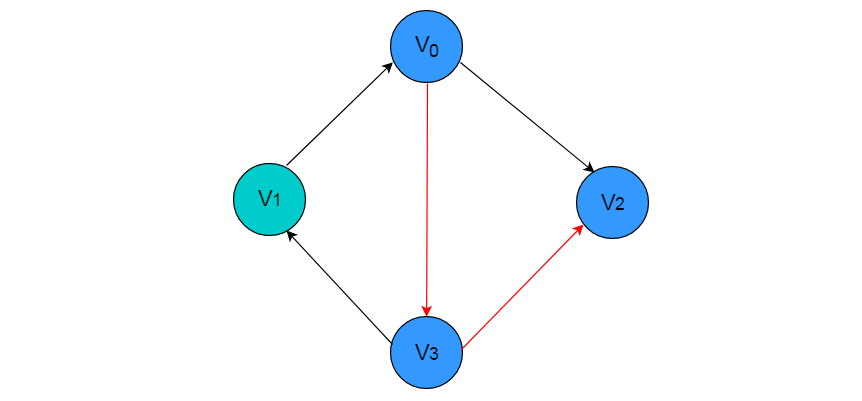
例如:在图 2.8 中所示图中依次访问顶点 V0 、V3 和 V2 ,则构成一条路径。
3 完全图
完全图:每个顶点都与其他顶点相邻接的图。
无向完全图:在无向图中,如果任意两个顶点之间都存在边,则称该图为无向完全图。(含有n个顶点的无向完全图有(n×(n-1))/2条边)
图 3.1 所示的图为无向完全图。

有向完全图:在有向图中,如果任意两个顶点之间都存在方向互为相反的两条边,则称该图为有向完全图。(含有 n 个顶点的有向完全图有 n×(n-1) 条边)
图3.2所示的图为有向完全图。

4 连通图
在无向图 G 中,如果从顶点 v 到顶点 v' 有路径,则称 v 和 v' 是连通的。 如果对于图中任意两个顶点 vi 、vj ∈E, vi,和vj都是连通的,则称 G 是连通图,否则图为非连通图。
例如:图4.1所示图,图中顶点A、B、C、D是连通的,但是其中任一顶点与顶点E或者顶点F之间没有路径,因此图4.1中所示的图为非连通图。
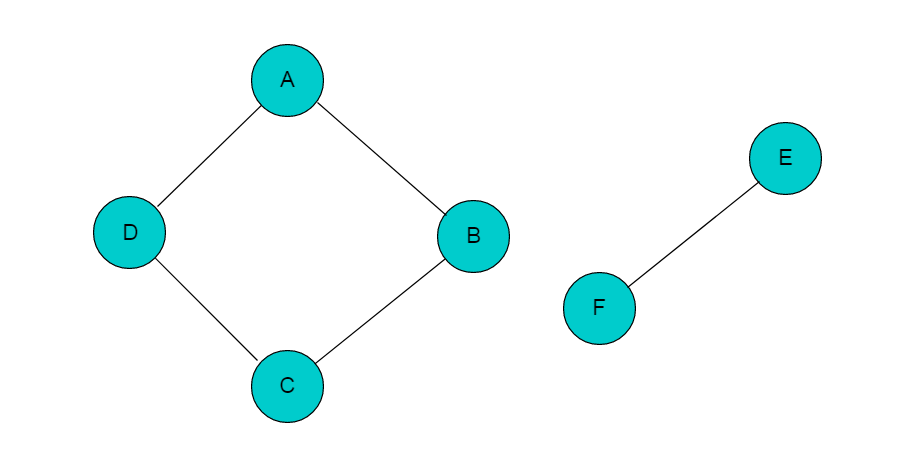
若添加顶点B与顶点F之间的邻接边,则图变为连通图,如图4.2所示:

5 数组存储
图的数组存储方式也称为邻接矩阵存储。图中的数据信息包括:顶点信息和描述顶点之间关系的边的信息,将这两种信息存储在数组中即为图的数组存储。
首先,创建顶点数组,顶点数组中存储的是图的顶点信息,采用一维数组的方式即可存储所有的顶点信息。存储图中边的信息时,由于边是描述顶点与顶点之间关系的信息,因此需要采用二维数组进行存储。
定义:设图 G 有 n 个顶点,则邻接矩阵是一个n X n的方阵A,定义为:

其中,
例如:下图所示的无向图,采用数组存储形式如下。

注:图中的数组存储方式简化了边的权值为 1 。
无向图的数组存储主要有以下特性:
(1)顶点数组长度为图的顶点数目n。边数组为n X n的二维数组。
(2)边数组中,A[i][j] =1代表顶点i与顶点j邻接,A[i][j] = 0代表顶点i与顶点j不邻接。
(3)在无向图中。由于边是无向边,因此顶点的邻接关系是对称的,边数组为对称二维数组。
(4)顶点与自身之间并未邻接关系,因此边数组的对角线上的元素均为0。
(5)顶点的度即为顶点所在的行或者列1的数目。例如:顶点V2的度为3,则V2所在行和列中的1的数目为3。
当图为有向图时,图的数组存储方式要发生变化。
例如:图5.2所示的有向图,采用数组存储形式如下。

有向图的数组存储主要有以下特性:
(1)顶点数组长度为图的顶点数目n。边数组为n X n的二维数组。
(2)边数组中,数组元素为1,即A[i][j] = 1,代表第i个顶点与第j个顶点邻接,且i为尾,j为头。 A[i][j] = 0代表顶点与顶点不邻接。
(3)在有向图中,由于边存在方向性,因此数组不一定为对称数组。
(4)对角线上元素为0。
(5)第i行中,1的数目代表第i个顶点的出度。例如:顶点V1的出度为2,则顶点V1所在行的1的数目为2。
(6)第j列中,1的数目代表第j个顶点的入度。例如:V3的入度为1,则V3所在列中1的数目为1。
数组存储方式优点:
数组存储方式容易实现图的操作。例如:求某顶点的度、判断顶点之间是否有边(弧)、找顶点的邻接点等等。
数组存储方式缺点:
采用数组存储方式,图若有n个顶点则需要n2个单元存储边(弧),空间存储效率为O(n2)。 当顶点数目较多,边数目较少时,此时图为稀疏图,这时尤其浪费空间。
例如:图5.3所示的图,图中有 9 个顶点,边数为10,需要 9X9 的二维数组,而实际存储边信息空间只有10,造成空间浪费。

图5.3所示无向图的存储数组:

6 邻接表
当使用数组存储时,主要有以下三个问题:
(1)对于一个图,若图中的顶点数目过大,则无法使用邻接矩阵进行存储。因为在分配数组内存时可能会导致内存分配失败。
(2)对于某些稀疏图(即顶点数目多,边数目少),创建的数组大小很大,而真正存储的有用信息又很少,这就造成了空间上的浪费。
(3)有时两个点之间不止存在有一条边,这是用邻接矩阵就无法同时表示两条以上的边。
针对以上情况,提出了一种特殊的图存储方式,让每个节点拥有的数组大小刚好就等于它所连接的边数,由此建立一种邻接表的存储方式。
邻接表存储方法是一种数组存储和链式存储相结合的存储方法。在邻接表中,对图中的每个顶点建立一个单链表,第 i 个单链表中的结点依附于顶点 Vi 的边(对有向图是以顶点Vi为尾的弧)。链表中的节点称为表节点,共有 3个域,具体结构见下图:
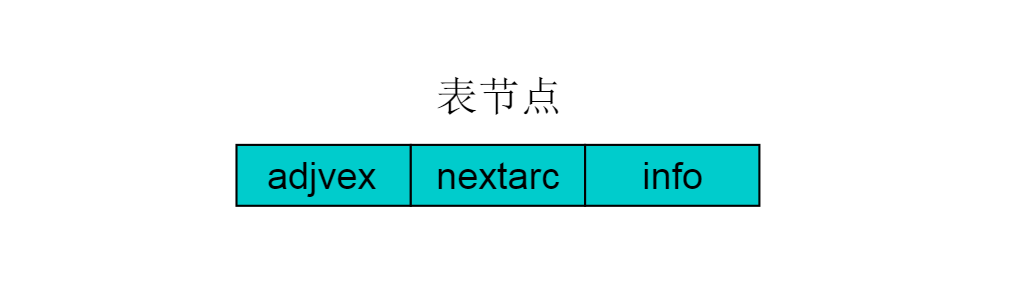
表结点由三个域组成,adjvex存储与Vi邻接的点在图中的位置,nextarc存储下一条边或弧的结点,data存储与边或弧相关的信息如权值。
除表节点外,需要在数组中存储头节点,头结点由两个域组成,分别指向链表中第一个顶点和存储Vi的名或其他信息。具体结构如下图:
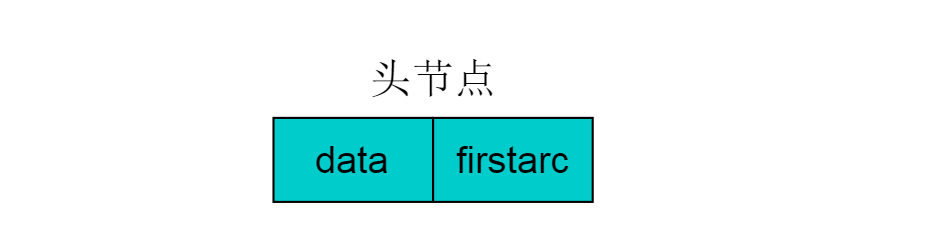
其中,data域中存储顶点相关信息,firstarc指向链表的第一个节点。
无向图采用邻接表方式存储
例如:图6.1所示的无向图采用邻接表存储。

采用邻接表方式存储图 6.1 中的无向图,绘图过程中忽略边节点的info信息,头结点中的 data 域存储顶点名称。以V1顶点为例,V1顶点的邻接顶点为V2、V3、V4,则可以创建3个表节点,表节点中adjvex分别存储V2、V3、V4的索引1、2、3,按照此方式,得到的邻接表为:
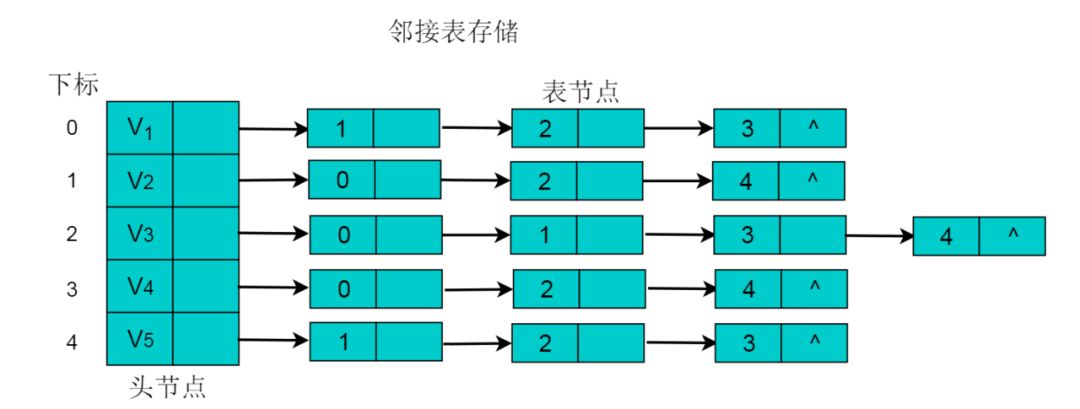
无向图的邻接表存储特性:
(1)数组中头节点的数目为图的顶点数目。
(2)链表的长度即为顶点的度。例如:V1顶点的度为3,则以V1为头节点的链表中表节点的数目为3。
有向图采用邻接表方式存储
例如:图 6.3 所示的有向图采用邻接表存储。

采用邻接表方式存储图6.3中的有向图,绘图过程中忽略边节点的info信息,头结点中的data域存储顶点名称。以V1顶点为例,V1顶点的邻接顶点为V2、V3、V4,但是以V1顶点为尾的边只有两条,即

有向图的邻接表存储特性:
(1)数组中表节点的数目为图的顶点数目。
(2)链表的长度即为顶点的出度。例如V1的出度为2,V1为头节点的链表中,表节点的数目为2。
(3)顶点Vi的入度为邻接表中所有adjvex值域为i的表结点数目。例如:顶点V3的入度为4,则链表中所有adjvex值域为2的表结点数目为4。
注:图采用邻接表的方式表示时,其表示方式是不唯一的。这是因为在每个顶点对应的单链表中,各边节点的链接次序可以是任意的,取决于建立邻接表的算法以及边的输入次序。
7 逆邻接表
在邻接表中,可以轻易的得出顶点的出度,但是想要得到顶点的入度,则需要遍历整个链表。为了便于确定顶点的入度,可以建立有向图的逆邻接表。逆邻接表的建立与邻接表相反。
采用逆邻接表的方式存储图3.2所示的无向图。以V3顶点为例,V3顶点的邻接顶点为V1、V2、V4、V5,以V3顶点为头的边有4条,即

8 十字链表
对于有向图而言,邻接链表的缺陷是要查询某个顶点的入度时需要遍历整个链表,而逆邻接链表在查询某个顶点的出度时要遍历整个链表。为了解决这些问题,十字链表将邻接链表和逆邻接链表综合了起来,而得到的一种十字链表。在十字链表中,每一条边对应一种边节点,每一个顶点对应为顶点节点。
顶点节点
顶点节点即为头节点,由3个域构成,具体形式如下:

其中,data域存储与顶点相关的信息,firstin和firstout分别指向以此顶点为头或尾的第一个边节点。
边节点
在边节点为链表节点,共有 5 个域,具体形式如下:

其中,尾域tailvex和头域headvex分别指向尾和头的顶点在图中的位置。链域hlink指向头相同的下一条边,链域tlink指向尾相同的下一条边。info 存储此条边的相关信息。
例如:图8.1所示的有向图,采用十字链表存储图方式。

采用十字链表的方式存储图8.1中的有向图,绘图过程忽略边节点中的info信息,表头节点中的data域存储顶点名称。以V1顶点为例,顶点节点的data域存储V1顶点名,firstin存储以V1顶点为头第一个边节点,以V1顶点为头边为
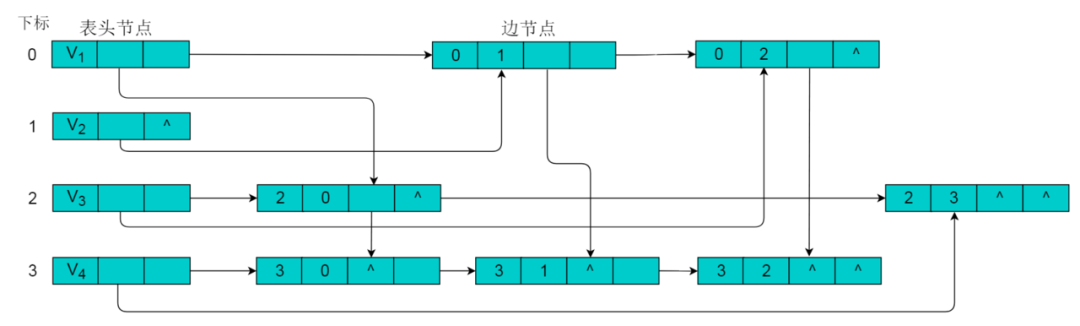
注:采用十字链表存储时,表头节点仍然使用数组存储,采用下标索引方式获取。
9 邻接多重表
对于无向图而言,其每条边在邻接链表中都需要两个结点来表示,而邻接多重表正是对其进行优化,让同一条边只用一个结点表示即可。邻接多重表仿照了十字链表的思想,对邻接链表的边表结点进行了改进。
重新定义的边结点结构如下图:

其中,ivex和jvex是指某条边依附的两个顶点在顶点表中的下标。 ilink指向依附顶点ivex的下一条边,jlink指向依附顶点jvex的下一条边。info存储边的相关信息。
重新定义的顶点结构如下图:
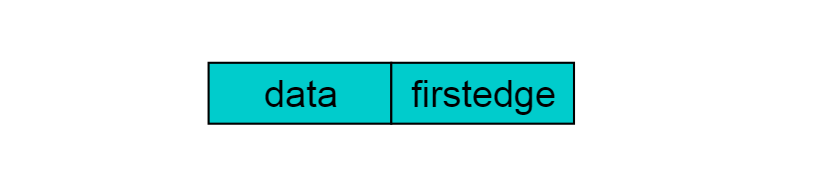
其中,data存储顶点的相关信息,firstedge指向第一条依附于该顶点的边。
例如:图9.1所示的无向图,采用邻接多重表存储图。
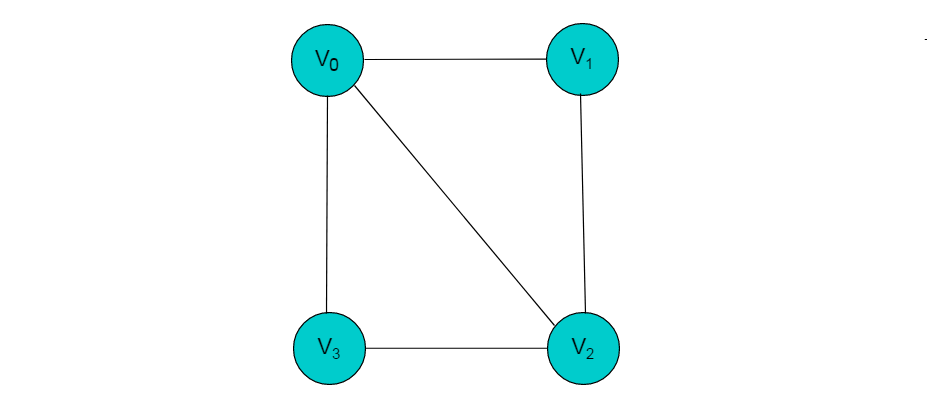
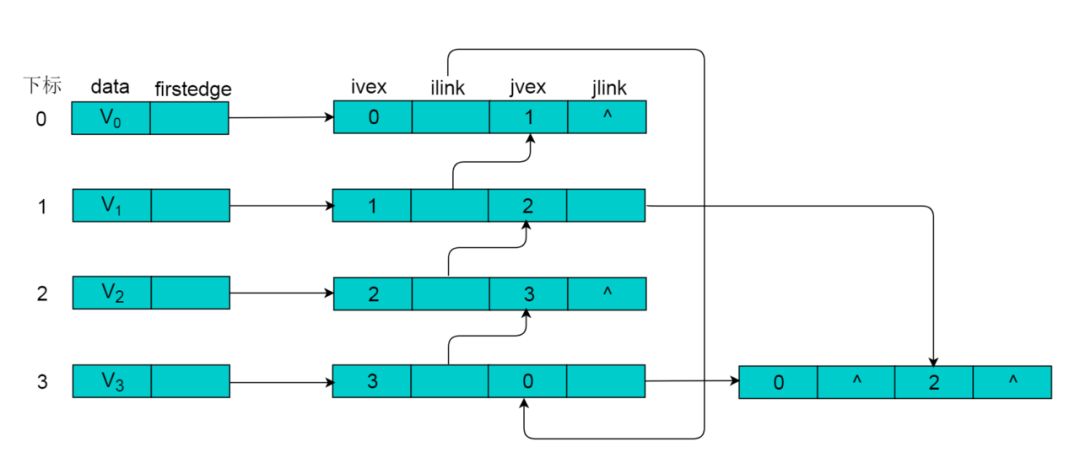
图 9.1 所示的无向图,采用邻接多重表存储,以 V0 为例,顶点节点的data域存储V0名称,firstedge 指向(V0 , V1)边,边节点中的ilink指向依附V0顶点的下一条边(V0 , V3),jlink指向依附V1顶点的下一条边(V1 , V2),按照此方式建立邻接多重表:
●编号881,输入编号直达本文
●输入m获取文章目录
程序员求职面试
更多推荐《25个技术类公众微信》
涵盖:程序人生、算法与数据结构、黑客技术与网络安全、大数据技术、前端开发、Java、Python、Web开发、安卓开发、iOS开发、C/C++、.NET、Linux、数据库、运维等。



