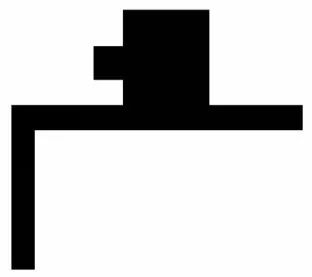人类如何从不同角度识别物体？你需要对「小样本学习」有所了解

来源：转载自公众号「雷克世界」微信号：ROBO_AI

编译：嗯~阿童木呀、多啦A亮

概要：在视觉层次结构的较低层次，不变性使你可以识别矩形或线条，即使它是倾斜、旋转或缩放的；而在更高的层次上，它可以让你识别人和物体，而无论视角、照明条件或背景环境。

之前，我们解释了视觉世界是由部分层次结构组成的。自行车由车把、车轮、踏板等构成；车轮由轮胎、轮辐、轮毂等组成；在物质世界的最低水平，一切都是由颜色、边缘、形状和纹理组成。在这种层次结构的每一层，我们的大脑在某种程度上都是不变的。在视觉层次结构的较低层次，不变性使你可以识别矩形或线条，即使它是倾斜、旋转或缩放的；而在更高的层次上，它可以让你识别人和物体，而无论视角、照明条件或背景环境。

相同两部分的三种排列方式

在上述图像中，这三个形状中的每一个都是相同的两个不变概念的排列。前两个我们可以识别为大写字母T，但第三个显然不是——即使它包含相同的部分。这告诉我们，不仅仅是定义一个对象的部分存在，还有它们之间的关系。第二个T仍然看起来像T，因为这两个部分仍然互相连接在同一个位置上，并且旋转到同一个程度。第三个不像T，因为各部分现在有不同的关系——它们以相反的方向旋转，并且加入到不同的相对位置上。

 

这使我们能够了解我们的大脑是如何运作的。首先，即使我们容忍差异，我们仍然可以看到变化。其次，我们可以描述这种变化是什么（旋转），这意味着我们将一个概念的改变作为一个独立的维度（旋转、平移、颜色、亮度等）来解构。最后，我们用于描述变化的维度在部分之间是常见的，我们可以将它们联系起来。为了证明这一点，尝试想象下面的图像，但将颜色更改为红色，并将其旋转90度。

  

想象一下黑色部分是红色的，整个旋转90度

 

你可能从未见过这种线条和形状的精确组合，但是你仍然可以很容易地想象它旋转，并以不同的颜色。 这意味着我们采用一组常用的变化维度来识别和想象物体如何从不同的角度看，而不必先从各个角度看它们。

 

2011年，Geoffrey Hinton、Alex Krishevsky和Sida Wang发表了一篇名为“Transforming Autoencoders”的论文，其中提出了一种理论，该理论被通常称为“胶囊理论（Capsules Theory）”。该论文证明，给定一组描述每个视觉概念如何转换的常见维度，网络可以准确地预测和分类输入的不可见变化，只能看到原始输入一次（或少量几次）。只有看见一次后对物体进行准确分类的能力被称为“小样本学习（one-shot learning）”，而且是人类可以自然而然地做的事情，但已被证明是难以在机器中复制出来。胶囊论文中描述的架构实现了小样本学习，但是需要转换变化的知识来训练系统。因此，将系统扩展到现实世界的视觉应用是非常困难的——因为我们根本无法获取所需的训练数据。

那么需要做些什么来创建一个具有更多可扩展性的胶囊架构？我们先来看看 “胶囊”是什么，以及它的作用。这是论文中对胶囊（capsule）的描述。

每个胶囊（capsule）都学会在一个观看条件和变形有限的空间内识别一个隐式定义的视觉实体，并且它会输出这个实体存在于其有限域内的概率以及和一组“实例化参数”，这里面可能包括精确的位姿、照明和该视觉实体相对于其隐式定义的规范版本的变形。

这真是一个相当密集、冗长的句子，但它意味着每个胶囊都代表一种视觉概念，这种概念在当诸如照明、视角等发生一定程度的变化时仍然保持不变。如果这个部分听起来很熟悉，不要怀疑，因为它正是我们在本文前面的部分所展示过的。还有一点是前文演示中没有提到，但胶囊可以做到的是随着变化的维度“实例化参数”。换句话说，它不仅可以识别出目标的存在，还可以确定其精确位置，如旋转角度、大小等。

其实，胶囊的架构主要依赖于训练期间所发生的转化变化的先验知识，但是当我们人类自身学着观察的时候，我们并没有给这些变化标上标签。我们能够简单地通过观察将我们能够将我们的视觉世界解构为一组常见的变化维度，如位置、光线条件和旋转。这一点与我们在上一篇文章中所提出的观点有些相似，我们建议人类利用情景性或顺序性数据来进行维度分离。

在我们以前的演示中，我们展示了这些片段可用于将视觉概念的所有变体分组到多个流形检测器中。在我们的架构中，每个流形都可以在其所有变体中检测到一个视觉概念，但它并没有给出关于当前变体的任何信息。它可能会告诉我们“在这个图像中有一个正方形”但不会告诉我们“正方形旋转了10度左右，相对较大，且位于图像的左下角附近”。下面的演示展示了我们该如何创造性地构建流形检测器，从而使得它能够使用情景性数据来提供这些信息。换句话说，我们如何将流形检测器架构转变成一个更具扩展性的胶囊版本。

下面是一个流形以不同位置和旋转度表示心形的示例。3d可视化中的每个点代表心形的一个特定版本。最初系统是无序的，所以移动滑块并不会产生任何有用的东西，但经过一些训练（按下播放）之后，它就会自动排序，发现潜在的隐含维度。一旦组织起来，这些滑块就代表了一个变化的单一维度。