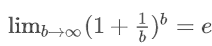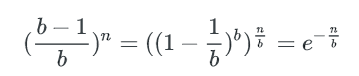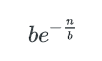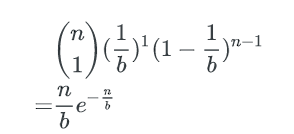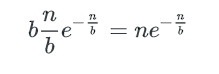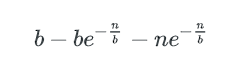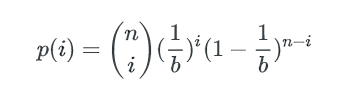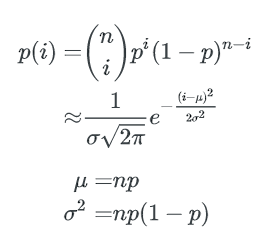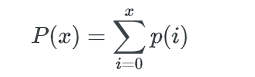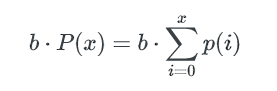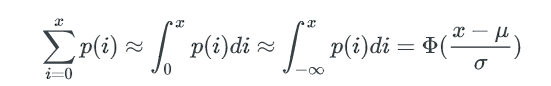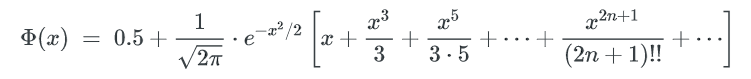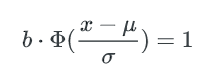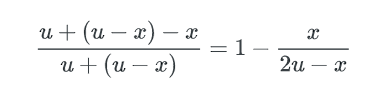程序员必读：摸清hash表的脾性

2017 年 9 月 6 日 CSDN 张炎泼

作者：张炎泼（XP），白山云科技合伙人兼研发副总裁，绰号XP。

张炎泼先生于2016年加入白山云科技，主要负责对象存储研发、数据跨机房分布和修复问题解决等工作。以实现100PB级数据存储为目标，其带领团队完成全网分布存储系统的设计、实现与部署工作，将数据“冷”“热”分离，使冷数据成本压缩至1.2倍冗余度。

张炎泼先生2006年至2015年，曾就职于新浪，负责Cross-IDC PB级云存储服务的架构设计、协作流程制定、代码规范和实施标准制定及大部分功能实现等工作，支持新浪微博、微盘、视频、SAE、音乐、软件下载等新浪内部存储等业务；2015年至2016年，于美团担任高级技术专家，设计了跨机房的百PB对象存储解决方案：设计和实现高并发和高可靠的多副本复制策略，优化Erasure Code降低90%IO开销。

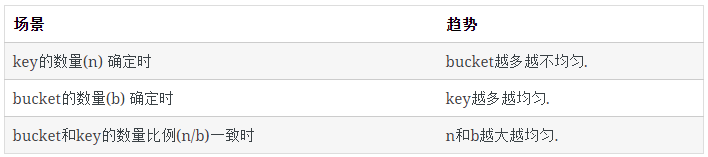
软件开发中，一个hash表相当于把n个key随机放入到b个bucket中，以实现n个数据在b个单位空间的存储。

我们发现hash表中存在一些有趣现象：

hash表中key的分布规律

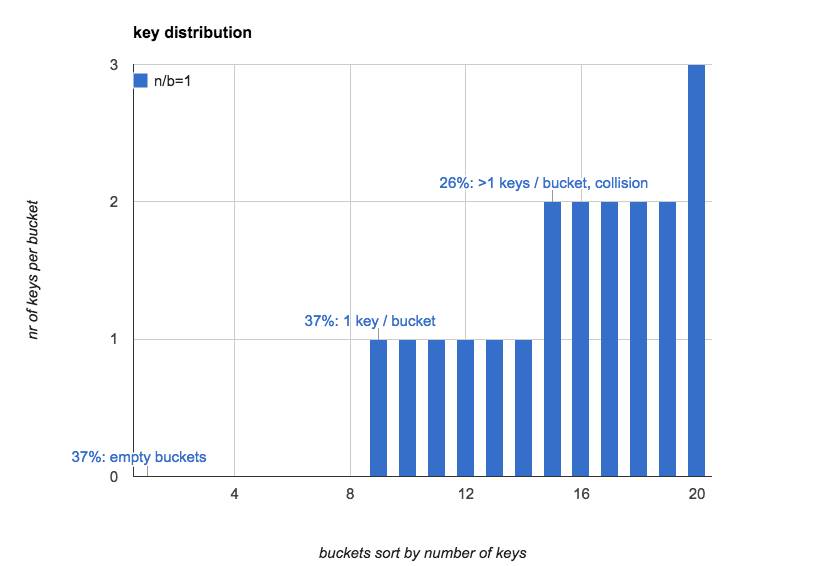
当hash表中key和bucket数量一样时（n/b=1）：

37% 的bucket是空的
37% 的bucket里只有1个key
26% 的bucket里有1个以上的key(hash冲突)

下图直观的展示了当n=b=20时，hash表里每个bucket中key的数量（按照key的数量对bucket做排序）：

往往我们对hash表的第一感觉是：如果将key随机放入所有的bucket，bucket中key的数量较为均匀，每个bucket里key数量的期望是1。

而实际上，bucket里key的分布在n较小时非常不均匀；当n增大时，才会逐渐趋于平均。

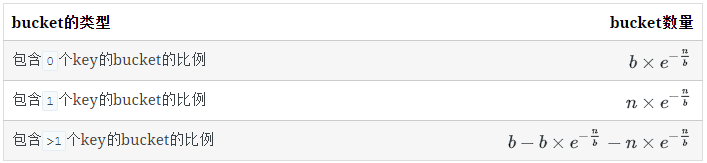
key的数量对3类bucket数量的影响

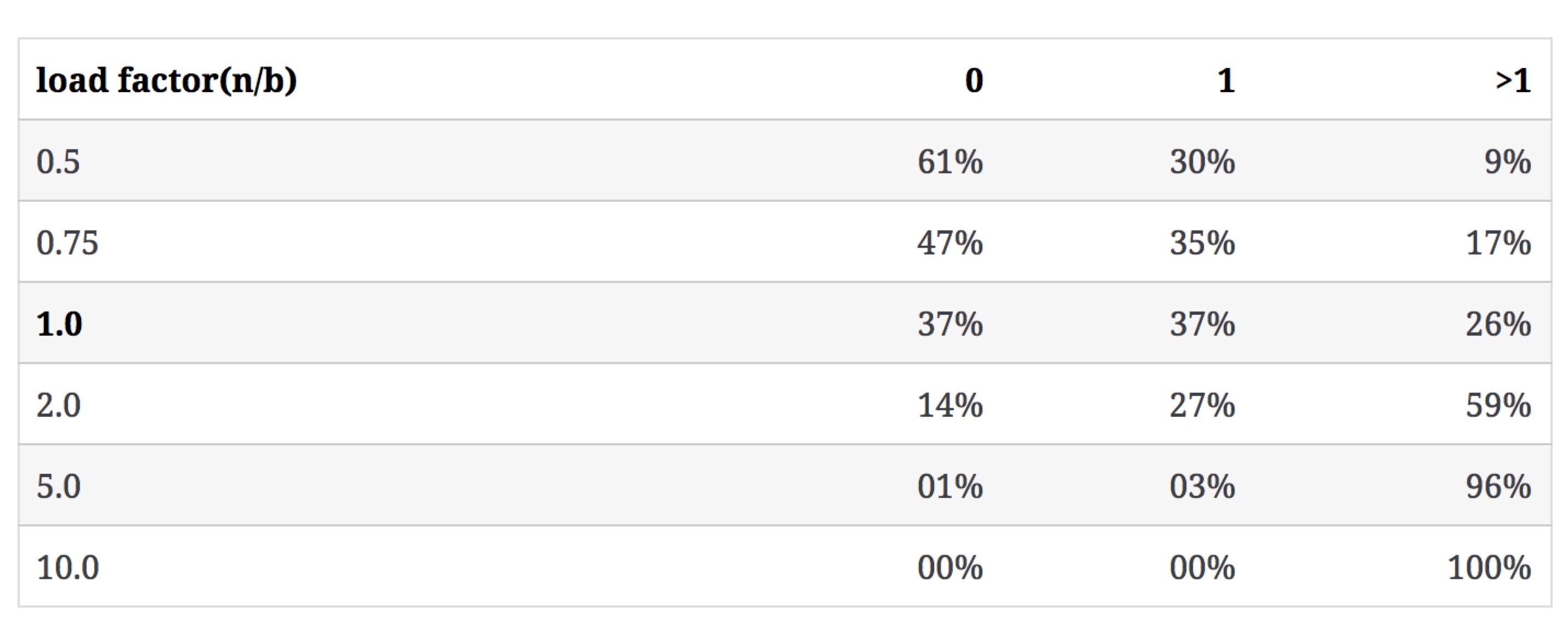
下表表示当b不变，n增大时，n/b的值如何影响3类bucket的数量占比（冲突率即含有多于1个key的bucket占比)：

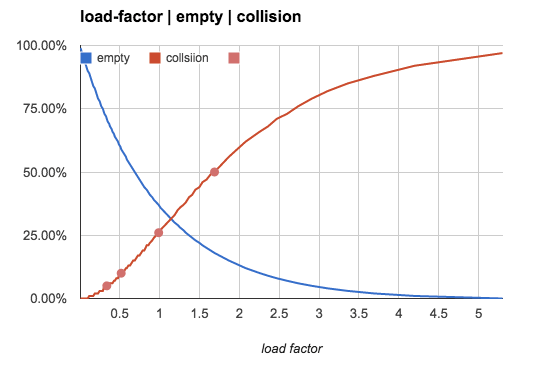
更直观一点，我们用下图来展示空bucket率和冲突率随n/b值的变化趋势：

key数量对bucket均匀程度的影响

上面几组数字是当n/b较小时有意义的参考值，但随n/b逐渐增大，空bucket与1个key的bucket数量几乎为0，绝大多数bucket含有多个key。

当n/b超过1（1个bucket允许存储多个key)，我们主要观察的对象就转变成bucket里key数量的分布规律。

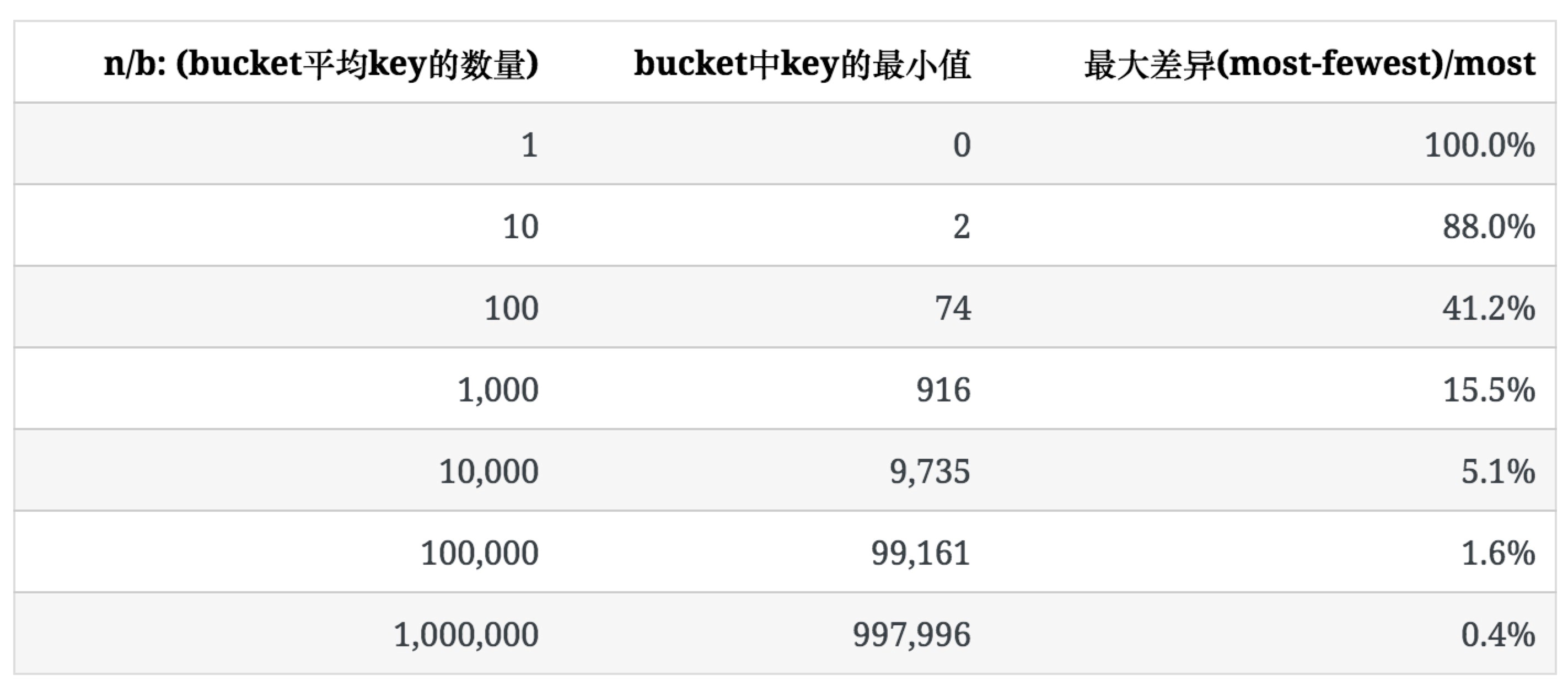
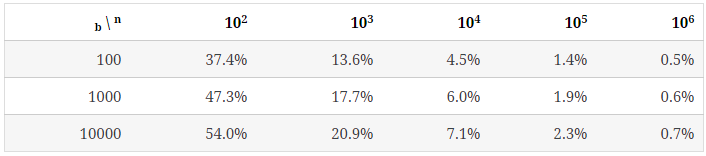
下表表示当n/b较大，每个bucket里key的数量趋于均匀时，不均匀的程度是多少。

为了描述这种不均匀的程度，我们使用bucket中key数量的最大值和最小值之间的比例（(most-fewest)/most)来表示。

下表列出了b=100时，随n增大，key的分布情况。

可以看出，随着bucket里key平均数量的增加，其分布的不均匀程度也逐渐降低。

和空bucket或1个key的bucket的占比不同n/b，均匀程度不仅取决于n/b的值，也受b值的影响，后面会提到。

未使用统计中常用的均方差法去描述key分布的不均匀程度，是因为软件开发过程中，更多时候要考虑最坏情况下所需准备的内存等资源。

Load Factor：n/b<0.75

hash表中常用一个概念 load factor α=n/b，来描述hash表的特征。

通常，基于内存存储的hash表，它的 n/b ≤0.75。这样设定，既可节省空间，也可以保持key的冲突率相对较低，低冲突率意味着低频率的hash重定位，hash表的插入会更快。

线性探测是一个经常被使用的解决插入时hash冲突的算法，它在1个bucket出现冲突时，按照逐步增加的步长顺序向后查看这个bucket后面的bucket，直到找到1个空bucket。因此它对hash的冲突非常敏感。

在n/b=0.75 这个场景中，如果不使用线性探测（譬如使用bucket内的链表来保存多个key)，大约有47% 的bucket是空的；如果使用线性探测，这47%的bucket中，大约一半的bucket会被线性探测填充。

在很多内存hash表的实现中，选择n/b＝<=0.75作为hash表的容量上限，不仅是考虑到冲突率随n/b增大而增大，更重要的是线性探测的效率会随着n/b的增大而迅速降低。

hash表特性小贴士：

hash表本身是一个通过一定的空间浪费来换取效率的算法。低时间开销(O(1))、低空间浪费、低冲突率，三者不可同时兼得；
hash表只适合纯内存数据结构的存储：

hash表通过空间浪费换取了访问速度的提升；磁盘的空间浪费是无法忍受的，但对内存的少许浪费是可接受的；
hash表只适合随机访问快的存储介质。硬盘上的数据存储更多使用btree或其他有序的数据结构。

多数高级语言（内建hash table、hash set等)都保持 n/b≤<=0.75；

hash表在n/b较小时，不会均匀分配key。

Load Factor：n/b>1

另外一种hash表的实现，专门用来存储比较多的key，当 n/b>1n/b1.0时，线性探测失效（没有足够的bucket存储每个key)。这时1个bucket里不仅存储1个key，一般在一个bucket内用chaining，将所有落在这个bucket的key用链表连接起来，来解决冲突时多个key的存储。

链表只在n/b不是很大时适用。因为链表的查找需要O(n)的时间开销，对于非常大的n/b，有时会用tree替代链表来管理bucket内的key。

n/b值较大的使用场景之一是：将一个网站的用户随机分配到多个不同的web-server上，这时每个web-server可以服务多个用户。多数情况下，我们都希望这种分配能尽可能均匀，从而有效利用每个web-server资源。

这就要求我们关注hash的均匀程度。因此，接下来要讨论的是，假定hash函数完全随机的，均匀程度根据n和b如何变化。

n/b 越大，key的分布越均匀

当 n/b 足够大时，空bucket率趋近于0，且每个bucket中key的数量趋于平均。每个bucket中key数量的期望是：

avg=n/b

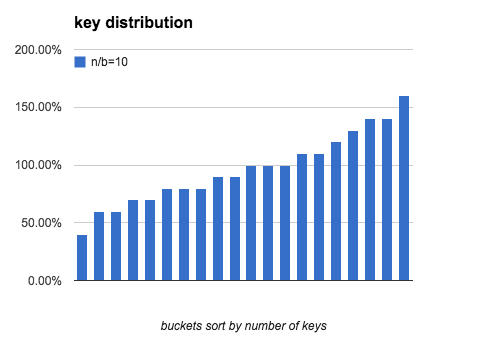
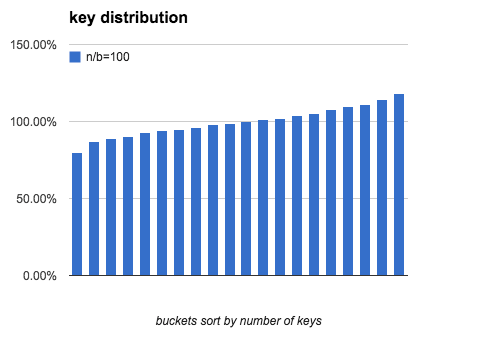
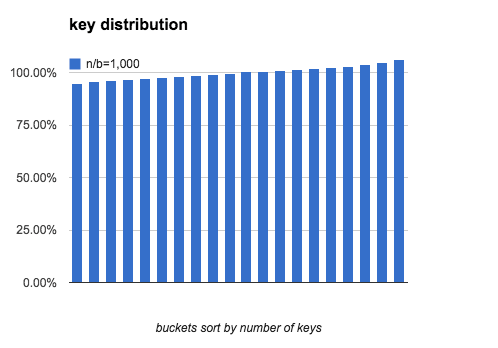
定义一个bucket平均key的数量是100%：bucket中key的数量刚好是n/b，下图分别模拟了 b=20，n/b分别为 10、100、1000时，bucket中key的数量分布。

可以看出，当 n/b 增大时，bucket中key数量的最大值与最小值差距在逐渐缩小。下表列出了随b和n/b增大，key分布的均匀程度的变化：

结论：

计算

上述大部分结果来自于程序模拟，现在我们来解决从数学上如何计算这些数值。

每类bucket的数量

空bucket数量

对于1个key, 它不在某个特定的bucket的概率是 (b−1)/b

所有key都不在某个特定的bucket的概率是( (b−1)/b)n

已知：

空bucket率是：

空bucket数量为：

有1个key的bucket数量

n个key中，每个key有1/b的概率落到某个特定的bucket里，其他key以1-(1/b)的概率不落在这个bucket里，因此，对某个特定的bucket，刚好有1个key的概率是：

刚好有1个key的bucket数量为：

多个key的bucket

剩下即为含多个key的bucket数量：

key在bucket中分布的均匀程度

类似的，1个bucket中刚好有i个key的概率是：n个key中任选i个，并都以1/b的概率落在这个bucket里，其他n-i个key都以1-1/b的概率不落在这个bucket里，即：

这就是著名的二项式分布。

我们可通过二项式分布估计bucket中key数量的最大值与最小值。

通过正态分布来近似

当 n, b 都很大时，二项式分布可以用正态分布来近似估计key分布的均匀性：

p=1/b，1个bucket中刚好有i个key的概率为：

1个bucket中key数量不多于x的概率是：

所以，所有不多于x个key的bucket数量是：

bucket中key数量的最小值，可以这样估算: 如果不多于x个key的bucket数量是1，那么这唯一1个bucket就是最少key的bucket。我们只要找到1个最小的x，让包含不多于x个key的bucket总数为1, 这个x就是bucket中key数量的最小值。

计算key数量的最小值x

一个bucket里包含不多于x个key的概率是：

Φ(x) 是正态分布的累计分布函数，当x-μ趋近于0时，可以使用以下方式来近似：

这个函数的计算较难，但只是要找到x，我们可以在[0~μ]的范围内逆向遍历x，以找到一个x 使得包含不多于x个key的bucket期望数量是1。

x可以认为这个x就是bucket里key数量的最小值，而这个hash表中，不均匀的程度可以用key数量最大值与最小值的差异来描述: 因为正态分布是对称的，所以key数量的最大值可以用 μ + (μ-x) 来表示。最终，bucket中key数量最大值与最小值的比例就是：

（μ是均值n/b）

程序模拟

以下python脚本模拟了key在bucket中分布的情况，同时可以作为对比，验证上述计算结果。

import sys

import math

import time

import hashlib

def normal_pdf(x, mu, sigma):

x = float(x)

mu = float(mu)

m = 1.0 / math.sqrt( 2 * math.pi ) / sigma

n = math.exp(-(x-mu)**2 / (2*sigma*sigma))

return m * n

def normal_cdf(x, mu, sigma):

# integral(-oo,x)

x = float(x)

mu = float(mu)

sigma = float(sigma)

# to standard form

x = (x - mu) / sigma

s = x

v = x

for i in range(1, 100):

v = v * x * x / (2*i+1)

s += v

return 0.5 + s/(2*math.pi)**0.5 * math.e ** (-x*x/2)

def difference(nbucket, nkey):

nbucket, nkey= int(nbucket), int(nkey)

# binomial distribution approximation by normal distribution

# find the bucket with minimal keys.

#

# the probability that a bucket has exactly i keys is:

# # probability density function

# normal_pdf(i, mu, sigma)

#

# the probability that a bucket has 0 ~ i keys is:

# # cumulative distribution function

# normal_cdf(i, mu, sigma)

#

# if the probability that a bucket has 0 ~ i keys is greater than 1/nbucket, we

# say there will be a bucket in hash table has:

# (i_0*p_0 + i_1*p_1 + ...)/(p_0 + p_1 + ..) keys.

p = 1.0 / nbucket

mu = nkey * p

sigma = math.sqrt(nkey * p * (1-p))

target = 1.0 / nbucket

minimal = mu

while True:

xx = normal_cdf(minimal, mu, sigma)

if abs(xx-target) < target/10:

break

minimal -= 1

return minimal, (mu-minimal) * 2 / (mu + (mu - minimal))

def difference_simulation(nbucket, nkey):

t = str(time.time())

nbucket, nkey= int(nbucket), int(nkey)

buckets = [0] * nbucket

for i in range(nkey):

hsh = hashlib.sha1(t + str(i)).digest()

buckets[hash(hsh) % nbucket] += 1

buckets.sort()

nmin, mmax = buckets[0], buckets[-1]

return nmin, float(mmax - nmin) / mmax

if __name__ == "__main__":

nbucket, nkey= sys.argv[1:]

minimal, rate = difference(nbucket, nkey)

print 'by normal distribution:'

print ' min_bucket:', minimal

print ' difference:', rate

minimal, rate = difference_simulation(nbucket, nkey)

print 'by simulation:'

print ' min_bucket:', minimal

print ' difference:', rate