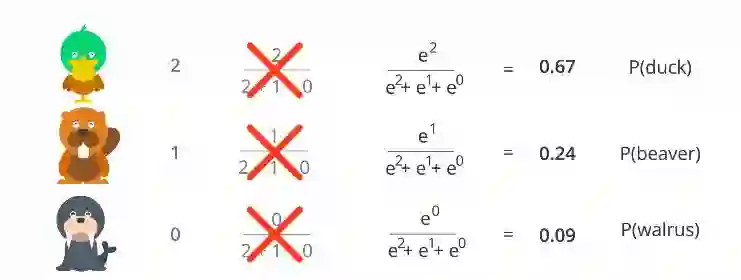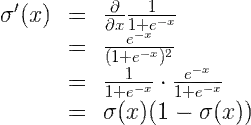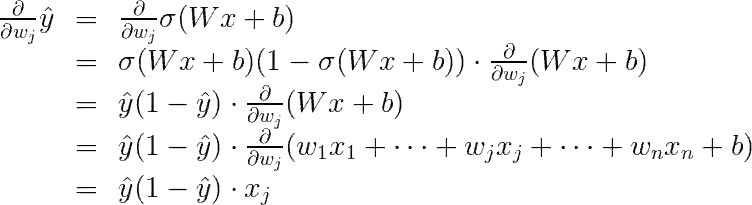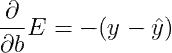用Pytorch做深度学习(第一部分)
本文为 AI 研习社编译的技术博客,原标题 :
Intro to Deep Learning with Pytorch - Part 1
作者 | Purnasai gudikandula
翻译 | 邓普斯•杰弗、shunshun
校对 | 酱番梨 整理 | 菠萝妹
原文链接:
https://medium.com/@purnasaigudikandula/intro-to-deep-learning-with-pytorch-part-1-53e111610575
注:本文的相关链接请点击文末【阅读原文】进行访问
用Pytorch做深度学习(第一部分)
这个博客是关于我从udacity pytorch奖学金挑战课程中学到的东西。
深度学习:
深度学习是机器学习的一个领域,利用大规模网络,海量数据集和在GPU(图形处理单元)上的加速运算。
机器学习 vs 深度学习
应用:
个人语音助理,医学成像,自动驾驶汽车,视频游戏AI等等。
内容包含:
深度学习背后的概念。
如何使用pytorch构建Deeplearning模型。
Pytorch:
Pytorch是来自facebook(facebook AI研究团队)的开源框架,用于开发深度神经网络。
你可以认为Pytorch是numpy的扩展,它有一些方便的定义,用于定义神经网络和使用GPU加速计算。
课程大纲:
本课程包含8节课和一个实验。8节课是
神经网络简介: 你将学习深度学习背后的概念以及我们如何使用反向传播训练深度神经网络。
与 soumith chintala 谈论 pytorch: soumith chintala , pytorch的创造者,谈论pytorch的过去,现在和未来。
pytorch简介: 您将学习如何使用pytorch构建深度神经网络,并使用预训练网络对狗和猫图像进行分类。
卷积神经网络: 您将学习卷积神经网络以及用于解决计算机视觉问题的强大的体系结构。
风格转换: 使用经过训练的网络将一个图像的样式转换为另一个图像并实现风格转换模型。
循环神经网络: 您将学习循环神经网络如何从时间序列等数据序列中进行学习的,并构建一个循环神经网络,从文本中学习并一次生成一个字符的新文本。
使用RNN的情感预测: 将建立和训练可以对电影评论的情感进行分类的循环网络。
部署pytorch模型: 将学习如何使用pytorch的混合前端将模型从pytorch转换为C++以用于生产。
实验: 从头开始构建一个深度学习模型,用于识别花卉图像的种类。你可以想象一个应用程序,告诉你你的相机正在拍的花的名称。在实践中,您将训练此分类器,然后将其导出以用于您的应用程序。
在训练和优化模型后,您将保存的网络上传到我们的工作区。您的模型将根据其测试集中预测花种的准确度得到分数。
该分数用于提供/不提供纳米学位。
第1课 - 神经网络介绍
深度学习有几个应用程序,如检测电子邮件中的垃圾邮件,预测股票价格,图片中的图像,医疗诊断,自动驾驶汽车等等。
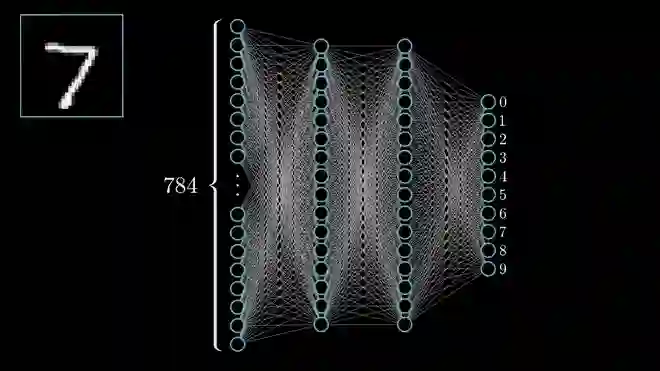
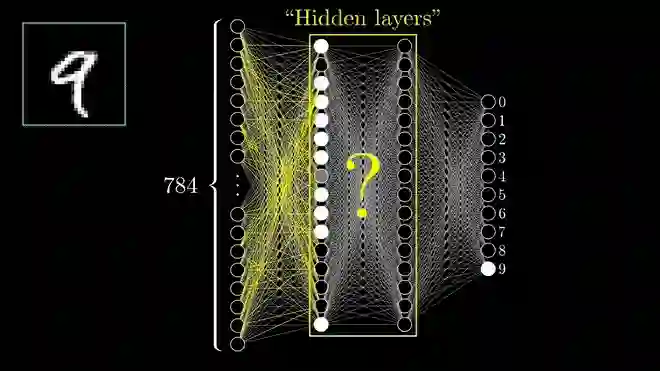
神经网络被认为是深度学习的核心。神经网络模糊地模仿了大脑如何运作的过程,神经元可以激发一些信息。深度神经网络具有大量节点,大量边缘,大量层,信息传递和遍历这些层。
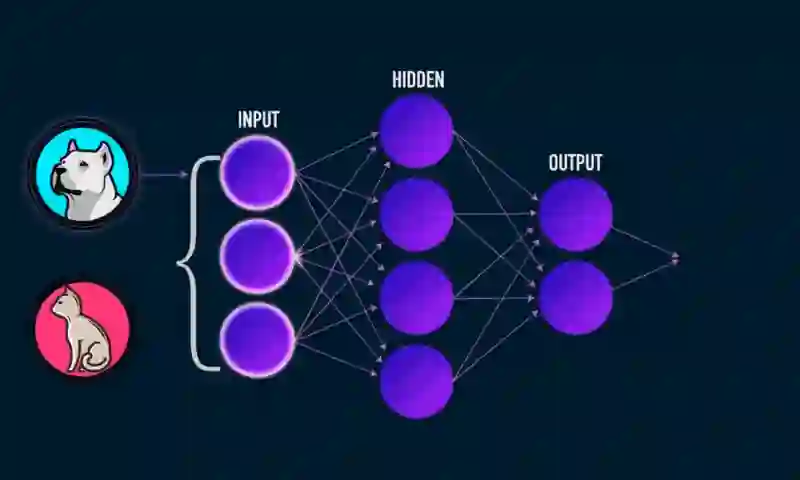
查看具有3层的简单神经网络,例如输入层,隐藏层和输出层。将图像猫/狗作为输入提供给网络/分类器,对给定图像进行分类,然后得到准确的输出,说明它是否是狗/猫。
深度神经网络对狗或猫进行分类
分类问题:
让我们举个例子。假设您是大学的录取官,您的工作是接受或拒绝申请。假设我们有3名学生,他们的成绩和考试成绩如下。
学生考试和成绩分数
在绘制图表上绘制这些点之后,如图所示:
绘制之后student1和student2的图形
在明确表示学生1被接受并且学生2被拒绝之后。现在可以说学生3会被接受吗?
线性边界:
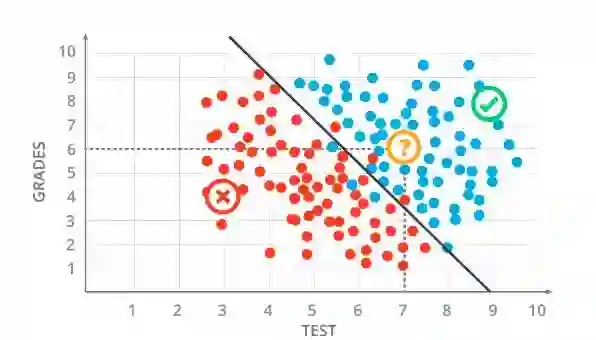
是的,学生3被接受了,因为如果你用给定的分数绘制图中的点,交叉点就会出现在蓝点区域。所以他被接受了。
线性模型的图形
如果我们在这些点之间绘制一条线,则清楚地表明直线上方的所有蓝色点都被接受,并且直线下方的红色点被拒绝。现在的问题是我们如何绘制这条线?通过观察它我们人类可以简单地绘制线条,但计算机将如何做。他们遵循几种算法来做到这一点。但不要忘记每个模型在分类时都会有一些错误。在上图中,即使在绘图之后,在线的上方和下方,模型也有几个蓝点和红点。
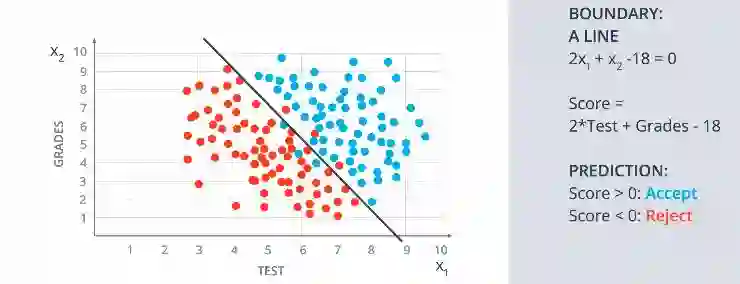
线性模型与一些方程
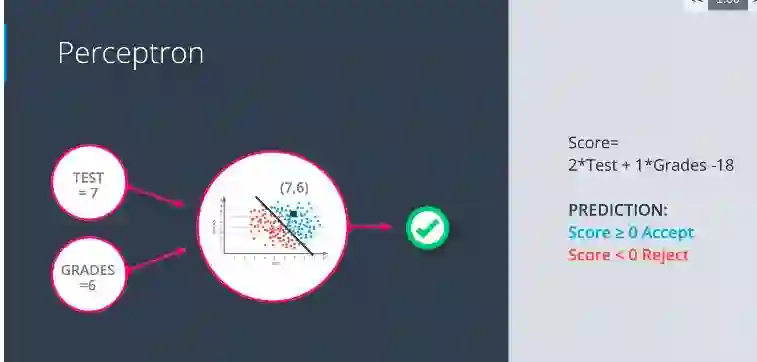
假设我们的线性模型有一些等式,分数用X2标记,考试成绩用X1标记。我们得到的线性模型(st线)是用下面的等式 2(x1) + (x2)- 18 =0 作为边界线。得分(y)是 Y= 2*Test +Grades- 18,如果我们想要绘制一条新线,预测值Y>0,那么学生就被接受。如果Y<0,那么学生将被拒绝。
一般来说,
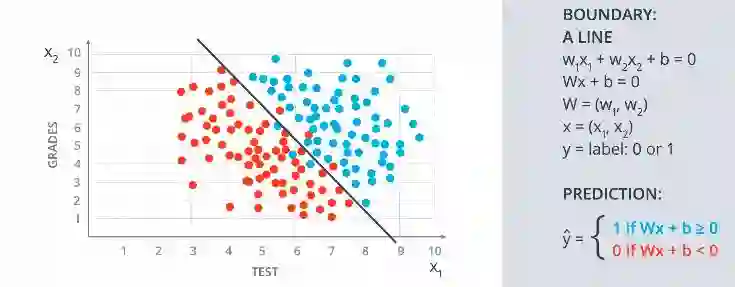
具有一般方程的线性模型
W 是具有点 W1 和 W2 的向量,X 也是具有 X1 和 X2 的向量。那么预测(y)是这两个向量的乘积加上偏差(b),它形成一个方程,y = Wx+ b。如果y =1,则接受,如果y=0,则拒绝。
更高的维度 :
现在如果我们有超过2个标签(grades, test)该怎么办?,如类别、等级。我们不会在二维工作。我们将在三维上展开。如下图
具有3个向量的高维图
如果我们有“n”个标签怎么办?然后那将是n维空间远超过2,如x1,x2,x3,x4,..., xn。
n维边界方程
感知机:
感知机是神经网络的一个重要组成部分,它只是将一个方程编码成一个小图。
感知机
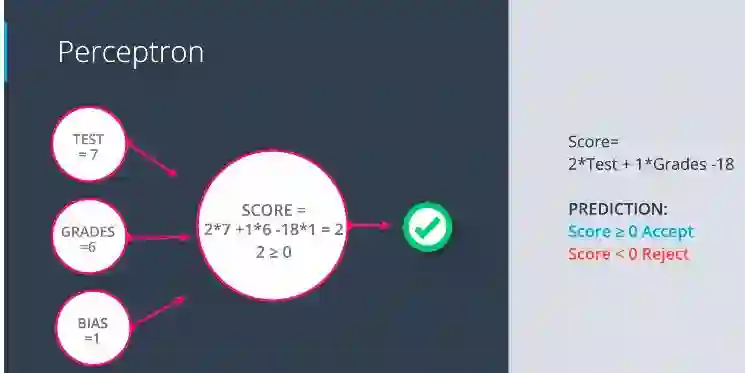
添加偏执后,如下图所示:
带有偏执的感知机
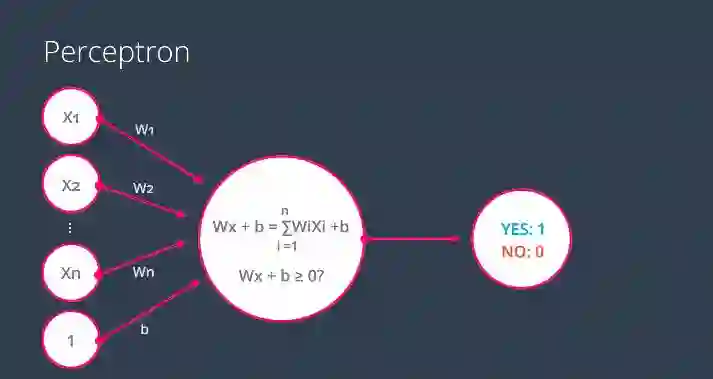
如果我们将带有“n”个权重的“n”个标签加上偏差“b”,那么简单地说就是2个向量的乘积加上偏差的求和形式。如果结果为1,则学生被接受否则被拒绝。看下面的图片。
带有n个标签的感知机
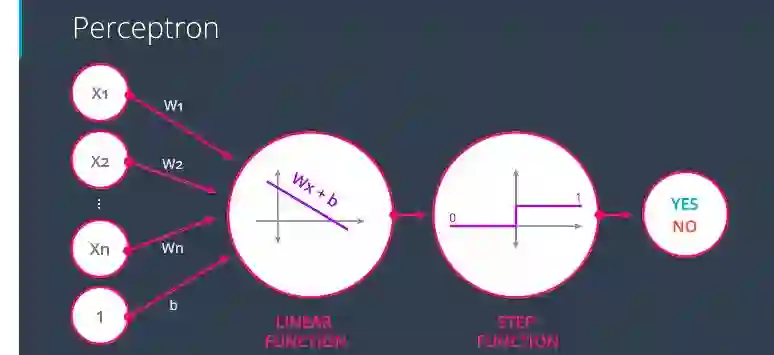
请注意,我们使用的是一个隐式函数,它被称为阶跃函数。
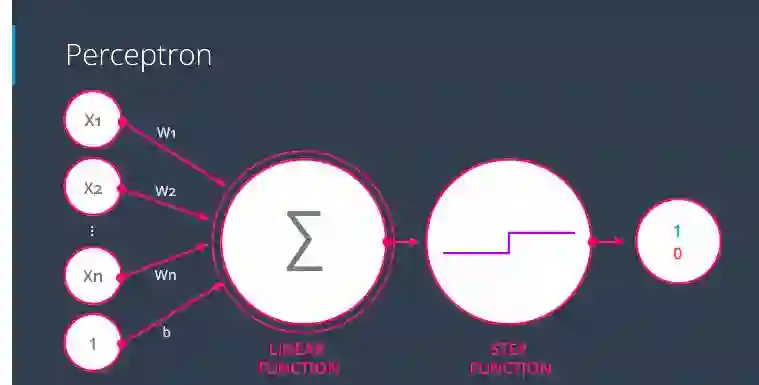
具有线性和阶跃函数的感知器
最后记住它的结构如下图:
为什么是“神经网络”?
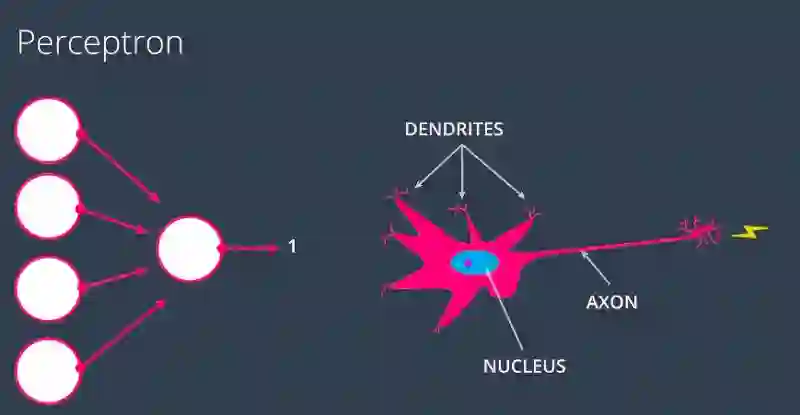
这些被称为神经网络的原因是感知器看起来像大脑中的神经元。
感知器类似于神经元
感知器作为逻辑运算符:
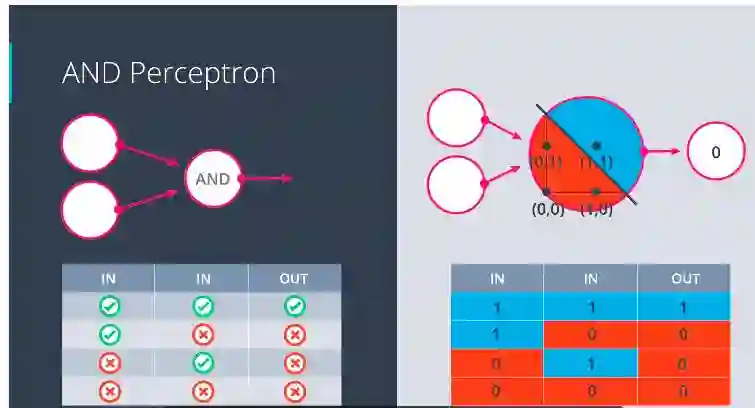
与(AND) 感知器:
具有“与”运算符的感知器
在“与”运算符中,如果两者都为真,则输出才为真。除此之外,每个组合都输出假。
注意: 不要在意输出节点中的零。
或(OR) 感知器:
具有“或”运算符的感知器
在“或”运算符中,如果任何一个组合为真(1),则输出将为真(1)。除此之外,每个组合都输出假。
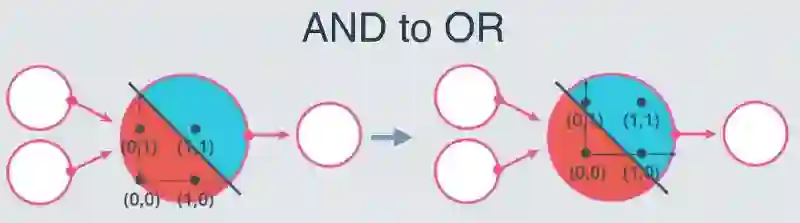
从“与”感知器到“或”感知器:
“与”到“或”
你能猜出从“与”感知器到“或”感知器应该怎么做么?
这里有两种从“与”感知器到“或”感知器的方法,它们可以通过增加权重或减少偏差的大小来实现。
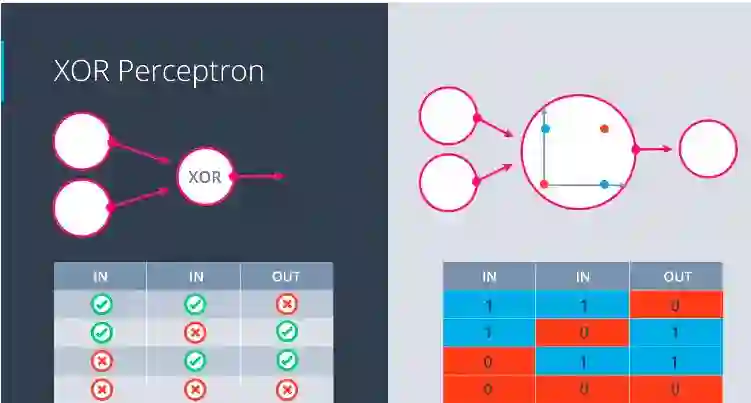
异或(XOR)感知器:
“异或”感知器
在“异或”运算中,一个为真(1),另一个为假(0),然后输出才为真(1)。除此之外,每个组合都输出假。
从“与”、“或”、“非”到"异或":
现在,让我们从“与”,“或”和“非”感知器构建一个多层感知器来创建逻辑“异或”!
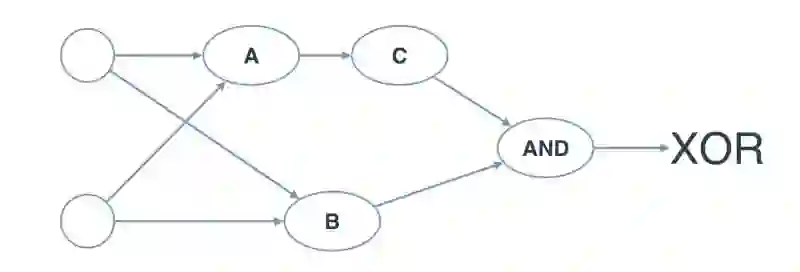
下面的神经网络包含3个感知器,A,B和C.最后一个(AND)已经为您提供。神经网络的输入来自第一个节点。输出来自最后一个节点。
下面的多层感知器计算XOR。每个感知器都是AND,OR和NOT的逻辑运算。但是,感知器A,B和C并不表示它们的操作。在以下测验中,为感知器设置正确的操作以计算XOR。
你能猜到A,B,C是什么吗?
在这里,A是AND,B是OR而C是NOT。在纸上试试这个并验证。
感知器技巧:
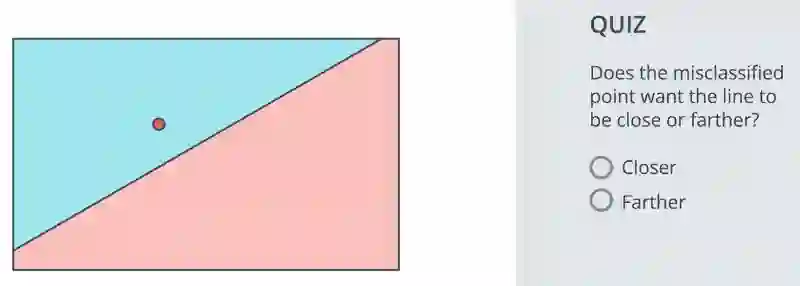
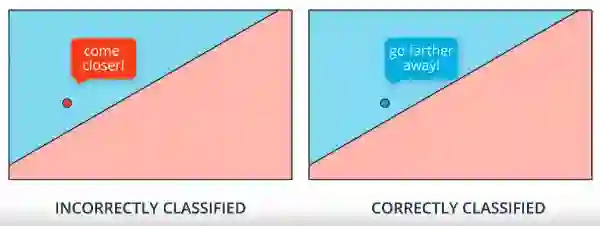
假设你有一个错误分类的点,你希望它被正确分类,那么你该怎么做?看下面的图片。
在这张照片中,很明显红点被错误分类。现在哪个选项使得错误分类点成为正确分类点。更近(Closer)还是更远(Farther)?
更近(Closer)
因为如果线越接近该点,那么这个点才有可能被正确分类,但不能通过移动使它远离。
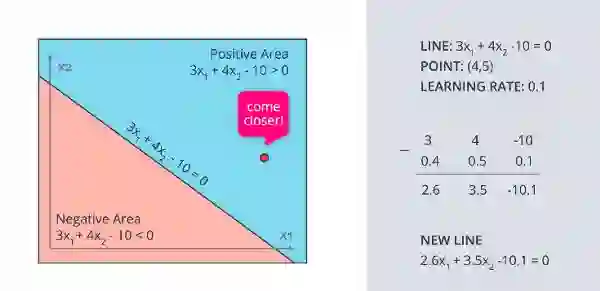
这里是感知器技巧,使线性模型正确地对点进行分类。
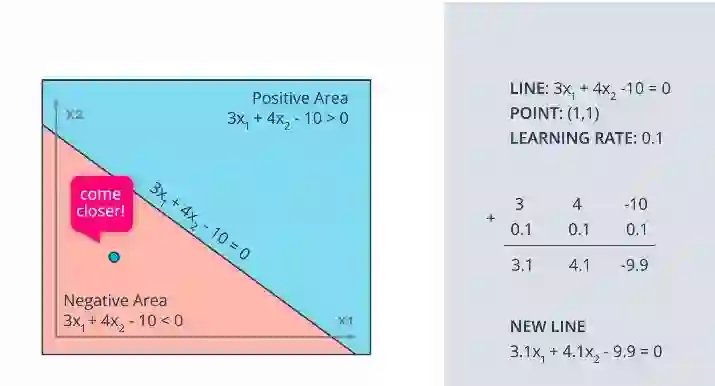
正如你在这里看到的,线性模型的公式为 3(x1) +4(x2) -10 =0,蓝色区域的点(4,5)显示为红色。这说明这个点是错误分类的。因此,重点在于“走近”,以便将这个点正确分类。因为该点在正区域,为了使其分类,我们必须从线的坐标中减去点和偏差,如图中所示。
但是这样做会给图形带来巨大的变化,可能会意外地错误地分类另一个点。我们希望这条线能够做出一个小小的动作来实现这一点,为此我们开始了解一个叫做学习率的术语。
在将学习率设为0.1后,将点值与学习率相乘,然后减去它。这导致新的线移近点。
以相同的方式,如果该点在负区域,则应用加法而不是减法。
感知器算法:
在上图中,除了圈出的点和线上的点之外,所有四个点都被正确分类。
因此,对于红色区域中的蓝点表示它被错误分类,如果预测表明它为0,则将权重加到与学习率相乘后得到的值。这里alpha是学习率。
并且对于蓝色区域中的红点表示它被错误分类,如果预测显示为1,则将权重减去与学习率相乘后的值。
算法如下:
import numpy as np
# Setting the random seed, feel free to change it and see different solutions.
np.random.seed(42)def stepFunction(t):
if t >= 0:
return 1
return 0def prediction(X, W, b):
return stepFunction((np.matmul(X,W)+b)[0])# The function should receive as inputs the data X, the labels y,
# the weights W (as an array), and the bias b,
# update the weights and bias W, b, according to the perceptron algorithm,
# and return W and b.
def perceptronStep(X, y, W, b, learn_rate = 0.01):
for i in range(len(X)):
y_hat = prediction(X[i],W,b)
if y[i]-y_hat == 1:
W[0] += X[i][0]*learn_rate
W[1] += X[i][1]*learn_rate
b += learn_rate
elif y[i]-y_hat == -1:
W[0] -= X[i][0]*learn_rate
W[1] -= X[i][1]*learn_rate
b -= learn_rate
return W, b# This function runs the perceptron algorithm repeatedly on the dataset,
# and returns a few of the boundary lines obtained in the iterations,
# for plotting purposes.
# Feel free to play with the learning rate and the num_epochs,
# and see your results plotted below.
def trainPerceptronAlgorithm(X, y, learn_rate = 0.01, num_epochs = 25):
x_min, x_max = min(X.T[0]), max(X.T[0])
y_min, y_max = min(X.T[1]), max(X.T[1])
W = np.array(np.random.rand(2,1))
b = np.random.rand(1)[0] + x_max
# These are the solution lines that get plotted below.
boundary_lines = []
for i in range(num_epochs):
# In each epoch, we apply the perceptron step.
W, b = perceptronStep(X, y, W, b, learn_rate)
boundary_lines.append((-W[0]/W[1], -b/W[1]))
return boundary_lines这是代码的核心部分。
def perceptronStep(X, y, W, b, learn_rate = 0.01):
for i in range(len(X)):
y_hat = prediction(X[i],W,b)
if y[i]-y_hat == 1:
W[0] += X[i][0]*learn_rate
W[1] += X[i][1]*learn_rate
b += learn_rate
elif y[i]-y_hat == -1:
W[0] -= X[i][0]*learn_rate
W[1] -= X[i][1]*learn_rate
b -= learn_rate
return W, b非线性区域:
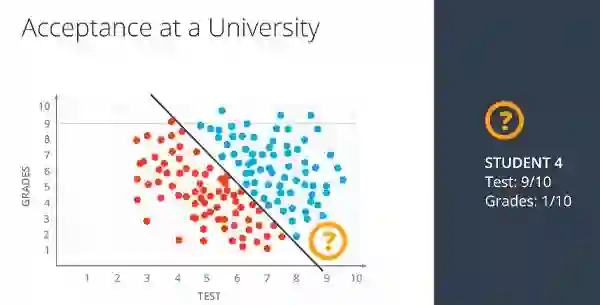
在这里你可以看到,根据当前模型已经接受了具有考试成绩9和成绩得分1的student4。但确切地说,这不应该发生。任何成绩不好的学生都不应被录取。
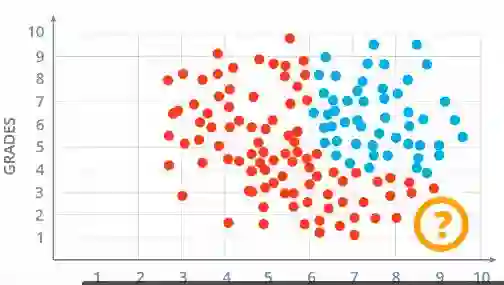
现在这个模型看起来更加真实,但正确分类这个模型的模型是什么?
蓝点(或)周围的圆形分隔蓝色和红色的曲线。让我们继续来看曲线。但不幸的是,这次感知器算法无法正常工作。
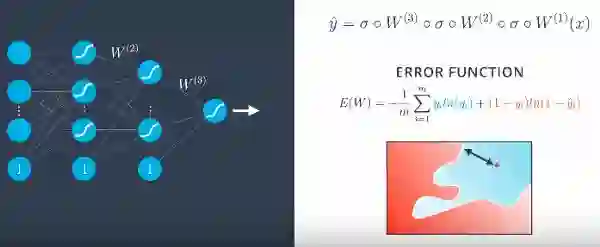
误差函数:
从现在开始,我们将看到具有误差函数的模型。这些模型正确地对点进行分类。误差函数只是告诉我们离解有多远。
假设你在登珠穆朗玛峰,你想要从顶部下山。那你要做什么?你会环顾四周,考虑所有可能的方向,然后我们选择让我们下降最快的方向。通过多次这样做,我们终于到达了珠穆朗玛峰的底部。这里我们用来解决问题的关键指标是作为误差的高度。误差告诉我们我们在运动中做得有多糟糕,以及我们与理想解的距离。
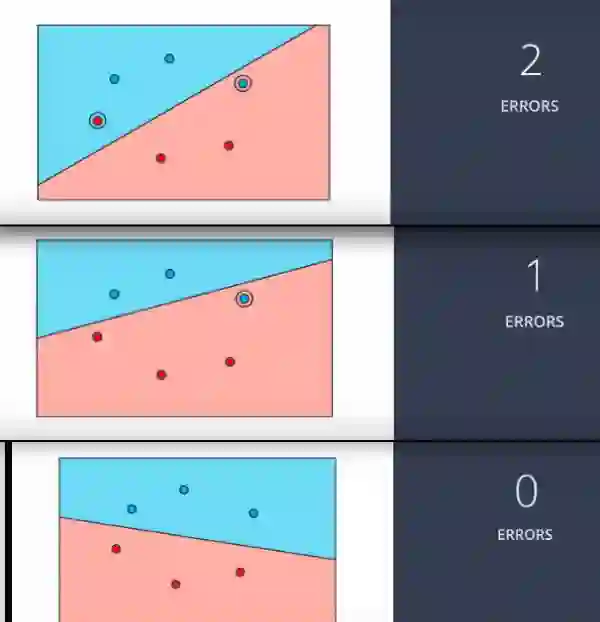
现在让我们对此图表采用相同的方法。在这里计算错误数量。这里有2个。
现在我们环顾所有方向来移动我们的线,使它可以减少错误。移动线后,我们在这里有1个错误。现在再看看并移动线以将误差减小到0.最后在移动线后我们得到0个错误。
但这种方法存在一个小问题。你知道我们的算法由于微积分需要非常小的步。我们的小步是通过使用导数产生的。这样做看起来像下图:
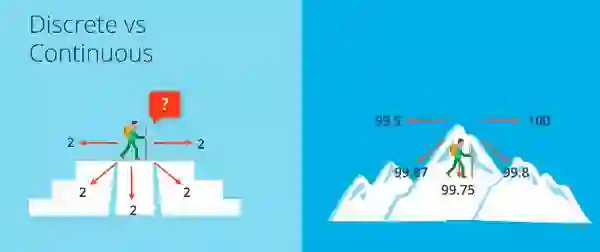
它就像从金字塔中下降一样,因为使用微积分会产生微小的运动,这会使我们的误差函数发生微小的变化,就像左边图中的值一样。为了使用梯度下降,我们的程序必须是连续的,就像珠穆朗玛峰一样,但不能像离散的那样可以从2到1然后从1到0进行突然的运动。
现在我有一个问题要问你。应用梯度下降应该满足哪些条件?
误差函数应该是连续的和可微的。
而且为了应用梯度下降,我们应该从离散预测转向连续预测。
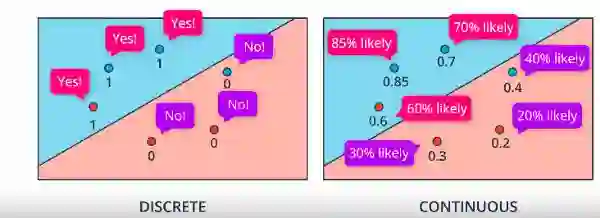
离散与连续:
在离散中,红色区域中的点为0,蓝色区域中的点为1。但是在连续的情况下,我们在红色区域中的点数值小于0.5,而在蓝色区域中的点数值大于0.5。
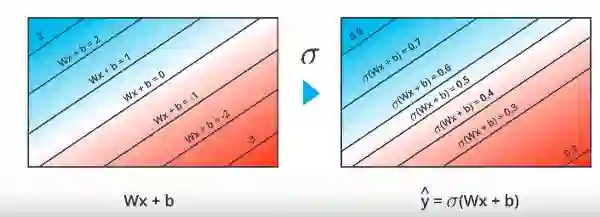
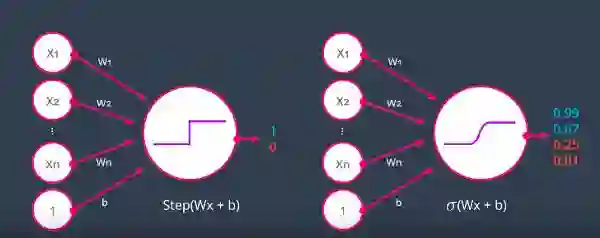
我们从离散到连续的方式是将激活函数从阶跃改为sigmoid函数。
在将sigmoid函数应用于离散形式的值3,2,1,0,-1,-2,-3之后,现在我们具有从0到1的值。
图左侧具有阶跃激活函数,输出值为0和1,右侧具有sigmoid激活函数,输出值范围在0到1。
多类分类和softmax:
到目前为止,我们已经看到模型给我们答案是/否或标签为正或负的概率。如果我们有更多的类别,比如狗,猫,鸟怎么办?
我们将学习softmax函数,当问题有3个或更多类时,它相当于sigmoid激活函数。
现在我们希望我们的模型能够获得鸭子,海狸和海象的概率。让我们假设我们有一些输入,比如它有一个喙?它可以住在水里吗?头发还是没头发?没有牙齿?使用所有这些输入,我们的模型给出了分数,例如鸭子duck = 2,海狸beaver = 1,海象walrus = 0。现在我们如何得到这些分数的概率?我们几乎没有问题,因为所有这些概率必须加到1,因为我们的鸭子的值大于海狸的值大于海象的值。现在我们应该以同样的方式获得概率。
这样做的简单方法是,让我们把它的得分除以所有得分的总和。这可能有效。但如果我们有负值怎么办?因为当我们有1 /(1 + 0 +( - 1))之类的值时,它可能会导致无穷大。看看左边的图。
那么即使我们有负值,我们怎么才能让这个想法发挥作用呢?
我有一个问题,什么函数将每个数字都转换为正数呢?
指数函数
sofmax函数:
应用指数函数后的方程
这解决了我们之前遇到的所有问题。这个函数叫做softmax函数。
一般来说,假设我们有一个线性函数,得分从Z1到Zn。那么类i的概率是exponent(Zi)/(exp(Z1) + exp(Z2) +
…..exp(Zn))
让我们在Python中编写Softmax函数的公式。
import numpy as np
def softmax(L):
expL = np.exp(L)
sumExpL = sum(expL)
result = []
for i in expL:
result.append(i*1.0/sumExpL)
return resultOne-hot编码:
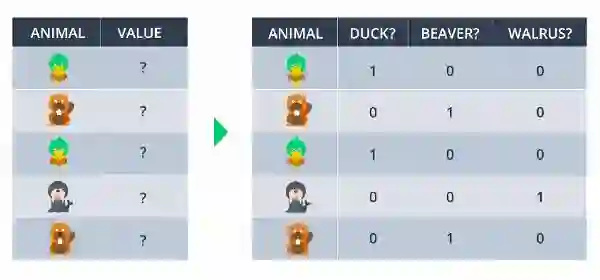
到目前为止,我们看到了输入数据为数字,但如果我们输入数据为鸟/非鸟(或)如果我们有更多的类别怎么办。
将这些值转换为1或0称作作为hot编码。
对于二分类它就像左边的那个,礼物为1而没有礼物为0.但如果我们有更多的类别怎么办?
如左图所示,如果我们有更多的类,那么为鸭子分配0,为海狸分配1,为海象分配2,但那不会起作用。它会产生一些依赖性问题。所以,如果动物是鸭子,那么只将1分配给你有鸭子的盒子,如果是海狸,那么将1分配给你有海狸的盒子。像这样你甚至可以解决“n”类的问题。
最大似然:
在我们进行深度学习时,概率将成为我们最好的朋友之一。我们将看到我们如何使用概率来评估(和改进!)我们的模型。
那么如果我们有2个具有2个不同概率的模型,我们如何对最佳模型进行分类。模型A有86%的可能获得大学录取,而模型B有55%的概率被录取。那么你怎么说哪种模型更好。
好吧,最好的模型是给我们发生的事件提供更高概率的模型,无论是被接受还是被拒绝。这是非常直观的。这称为最大似然。
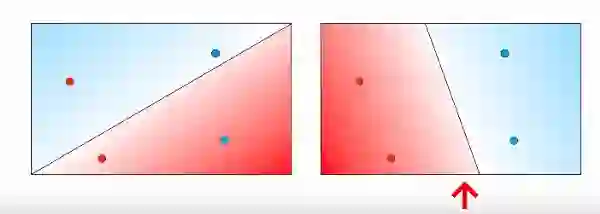
现在通过查看左边的图片,你能说出哪种型号看起来最好/准确吗?
是的,你是对的。与左侧相比,右侧的模型看起来相当不错。但是让我们做一些数学,然后相信右边的模型更好。
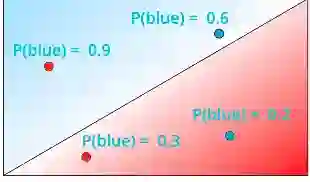
让我们说每个点为蓝色的概率如图所示。你知道红色的概率 = 1 - 蓝色概率。
所以现在对于2个蓝点,概率是0.6和0.2,而对于2个红点,概率是0.1和0.7。现在计算这些点的实际颜色的概率是乘以这些概率。由于这些概率是独立的,让我们将它们相乘,如下图所示。
对右边的模型做同样的事情并获得它的概率。在完成这个过程之后,这就是模型的概率。
因为我们知道似然最大的模型是最好的模型。所以右边的模型是最好的模型。
最大化概率:
因为我们知道给出最大值的模型是最好的。所以现在让我们最大化概率。我们之前也谈过误差函数,这个误差函数与最大化概率有什么关系吗?增加或减少任何一个取决于其他的变化?
现在我们需要做的就是最大化这些概率,但概率是数字的乘积。如果我们有更多的概率导致更多的分数怎么办?以及如果这些概率的一个值发生变化怎么办?然后整个概率发生变化。所以概率的乘积很差。现在使用和吧。
我有一个问题,什么函数将乘积变成和?
--
-
对数函数
是的,因为log(ab) = log(a) + log(b)
交叉熵 1:
应用自然对数后,每个概率都会产生一些负值。这是因为我们知道log 0和log1之间的值为负,因为log(1)=0。
现在,将这些对数的取反使他们变为正。这称为交叉熵。在左侧添加坏模型后,结果为4.8(高值),右侧的好模型为1.2(低值)。原因是最大值的负对数值低,反之亦然。
你可以清楚地观察到高值的负对数很低。错误分类的点的负对数具有巨大的误差值,例如2.3和1.61。
注意:较高的交叉熵意味着事件的概率较低。
现在我们的目标是最小化这个交叉熵。
交叉熵 2:
所以到了某个地方,概率与误差函数之间肯定存在联系,它被称为交叉熵。这个概念在很多领域都非常流行,包括机器学习。让我们深入研究公式,并实际编写代码!
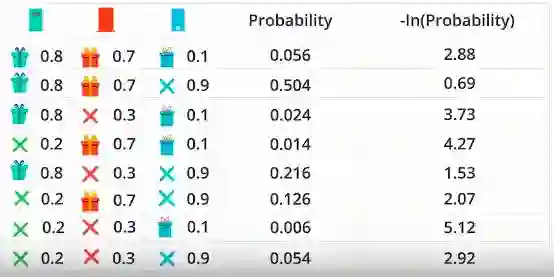
假设你给了3扇门,并且给出了有礼物或没有礼物的概率。由于有3个门,我们将获得8种情况。由于这些事件是独立的,因此给出了这些概率的乘积和这些概率的负对数。如果你在使用负对数后清楚地观察到高值的概率值很低。
使用变量导出公式,让我们取“p”和“y”。1-p是没有礼物而y = 0也是因为没有礼物,如图2所示。
现在,让我们在Python中编写交叉熵的公式。
import numpy as np
def cross_entropy(Y, P):
Y = np.float_(Y)
P = np.float_(P)
return -np.sum(Y * np.log(P) + (1 - Y) * np.log(1 - P))多类交叉熵:
这里给出了3扇门以及这些动物在门后的概率。在计算交叉熵后结果为2.48。
现在让我们概括一下,并在公式中加入一些变量。
现在给出了一些通用变量的公式,如图所示。
逻辑回归:
现在,我们终于开始机器学习中最流行和最有用的算法之一,以及构成深度学习的所有构建块。Logistic回归算法基本步骤是这样的:
取一些数据
选择一个随机模型
计算误差
最小化误差,获得一个更好的模型
Enjoy!
计算误差函数:
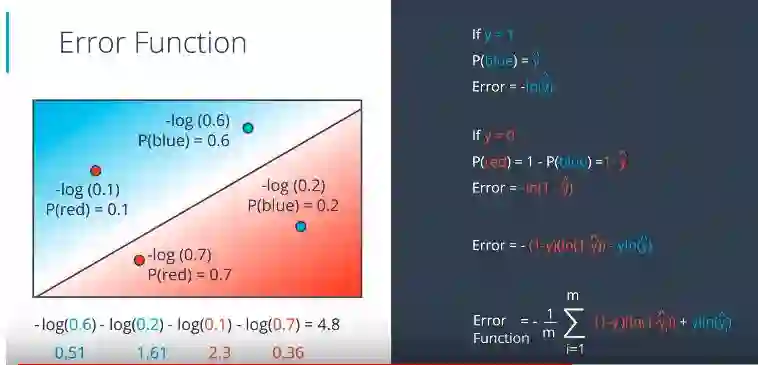
梳理一下我们今天学到的东西。就是如图所示计算误差函数的方法
这里如果y = 1,则表示点为蓝色的概率。如果y = 0,则表示点为红色的概率。并且我们知道误差是y_hat的负对数。在用图中计算公式计算误差函数之后,它输出4.8并且在平均之后我们得到每个点为1.2。
这里的误差函数看起来像是有礼物或没有礼物的二类熵和鸭子,海狸和海象的多类熵。
现在我们将学习梯度下降算法背后的原理和数学。
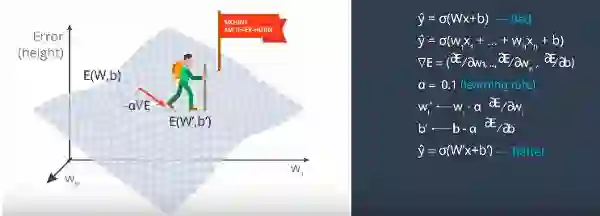
假设我们在顶部而且必须到底部。w1和w2是函数的输入。误差函数由E给出。然后,E的梯度作为E的偏导数相对于w1和w2的向量和给出。梯度实际上告诉我们想要移动的方向。所以我们采用误差函数的负梯度作为我们想要下降的方向移动。
我们知道预测(y hat) = sigmoid (Wx+b)。它很糟糕,因为我们在顶部有很大的误差函数。对于n 个权重,梯度对权重的偏导数作为误差函数的偏导数的向量形式给出。我们引入了alpha作为学习率。现在通过使用alpha与梯度相乘来更新权重,从顶部向下迈出一步。最后在更新yhat = sigmoid(w’x +b’)之后,会更好,因为误差更小。
我们了解到,为了最大限度地减少误差函数,我们需要应用一些导数。所以,让我们弄脏手,实际计算误差函数的导数。首先要注意的是,sigmoid函数有一个非常好的导数。也就是说,
σ′(x)=σ(x)(1−σ(x))
原因如下,我们可以使用商公式计算它:
最后一个等式是因为只计算wj的倒数,WJ XJ的导数为XJ。
现在,我们可以继续计算误差E相对于权重wj在点x处的的导数。
类似的计算将告诉我们:
感知器与梯度下降:
如果该点被错误分类,感知器和梯度下降都会使得线条更接近。但如果该点被正确分类,感知器不会做任何改变。但是梯度下降告诉线消失,因为如果该点在右侧区域,那么您将获得低错误率并且预测几乎= 1。
非线性模型:
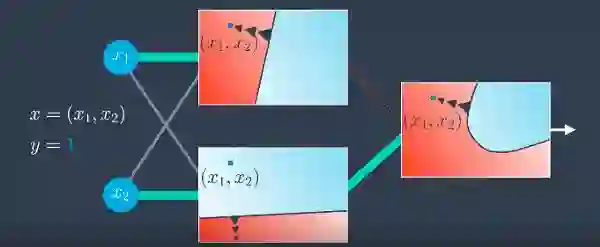
如果你看到这个,你可以说线性模型或线不能简单地划分数据。在这种情况下,我们主要考虑的是曲线。对于这样的数据,我们将创建一个概率函数,其中蓝色中的点更可能是蓝色,红色中的点更可能是红色,并且分离它们的曲线旁边有红色点也有蓝色点。所有都和前面一样,除了这个等式不是线性的。这是我们的神经网络发挥作用的地方。
神经网络架构:
好的,我们已准备好将这些块放在一起,并构建出色的神经网络!(或多层感知器。)
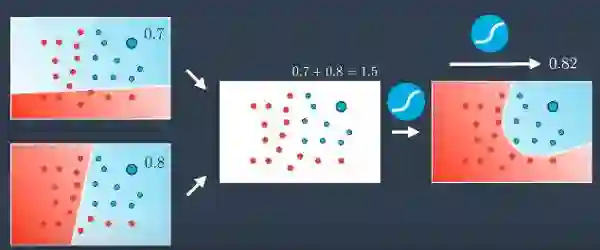
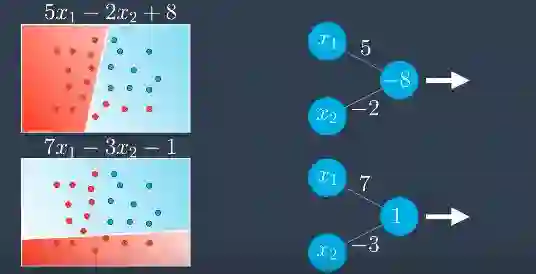
我们将结合2个线性模型来获得非线性模型。在这里,我们有一个点,蓝色的概率是0.7和0.8的两个模型。如果我们进行合并,那么我们得到一个高于1的值,即1.5。但是概率应该在0和1之间。所以我们应用sigmoid函数使值在0和1之间。
如果您希望第一个模型果对最终结果产生更大影响,该怎么办?这是怎么回事。
第一模型蓝色点的概率乘以7,即7 * 0.7,再加上第二模型蓝色点的概率乘以5,即5 * 0.8,再加上偏差-6得到2.9,这是交叉概率规则。应用sigmoid函数后,它是0.95。
某个值乘以常数或模型 + 某个值乘以另一个常数或模型 + bais = 形成非线性模型。
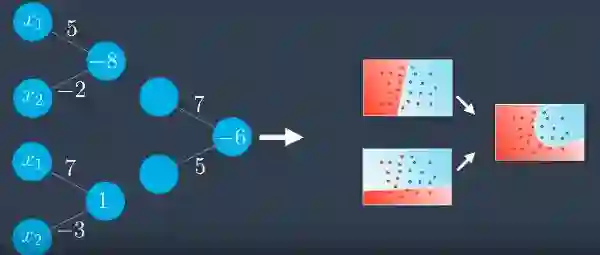
假设我们有2个不同的线性方程模型。如果我们在感知器中表示它们,它应该看起来像这样。
在为第一个和第二个模型中添加一些权重之后,在感知器中表示它们之后,它应该看起来像这样。
在加入这个之后我们得到了一些神经网络。
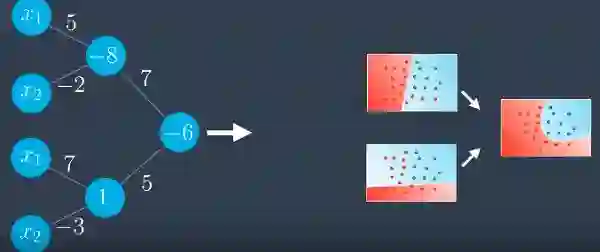
清洁一下后,它应该看起来像这样。
保留偏置节点的节点后,并应用sigmoid函数后,它看起来像左边的那个。
现在,并非所有神经网络都像上面那样。他们可能会更复杂!特别是,我们可以做以下事情:
向输入,隐藏和输出层添加更多节点。
添加更多层。
具有输入,隐藏和输出层的简单的神经网络。
这就是线性模型组合得到非线性模型的情况,如果这些非线性模型再次结合,便会形成更复杂的非线性模型。
这些复杂的模型是通过大量隐藏层获得的。这就是神经网络发生魔力的地方。现实生活中的自驾驾驶模型,游戏模型中有很多隐藏层。这个神经网络将用高度非线性的边界分裂n维空间,如顶部的那个。
我有一个问题,如果你试图对英文字母中的所有字母进行分类,你能猜出输出层中有多少个节点吗?
--
-
26
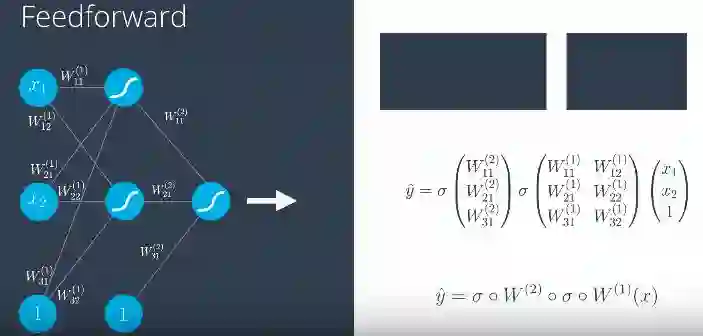
前馈:
前馈过程是神经网络中用于将输入转化为输出的过程。
为了训练神经网络,我们必须确定误差函数,对于输入向量为x1伴随着偏置输入到感知机输出至xn和权重为w1至wn的过程。
在应用sigmoid函数之后,如图所示,给出预测和误差函数。误差函数给出了测量点从直线分类的错误程度的度量。
即使在多层感知器中,除了预测(y ^)是通过权重矩阵并使用sigmoid函数获得,其他一切都保持不变。
反向传播:
简而言之,反向传播将包括:
进行前向传播操作。
将模型的输出与期望的输出进行比较。
计算误差。
进行反向传播以将误差分散到每个权重。
使用它来更新权重,并获得更好的模型。
继续直到我们有一个好的模型。
听起来比实际更复杂。
在做前向传播之后,模型应该像这样。但这并不好,因为仍然有点被错误分类。关键是要让曲线靠近点使其被正确分类。
如果隐藏层发生变化,可能会发生这种情况,在隐藏层中,第二个模型很好,因为它可以正确分类,但第一个模型不太好。
现在如果第二个模型的权重增加了怎么样?这有用么?是的,有些时候,只是在某种程度上有用。因此,我们可以通过增加或减少输出中的结果并进行一些校正来更新两个模型,希望能够得到正确的分类。
用一些有趣的照片来教你。
很快,第2部分和第3部分也将发布。
请点击喜欢,以促使我发布下一个部分
关注我以获取更新
如果你喜欢它,请与你的朋友分享。因为最好的总是应该分享。
感谢!
参考文献:
https://in.udacity.com/course/deep-learning-pytorch--ud188
https://www.youtube.com/watch?v=aircAruvnKk&list=PLLMP7TazTxHrgVk7w1EKpLBIDoC50QrPS
想要继续查看该篇文章相关链接和参考文献?
长按链接点击打开或点击底部【阅读原文】:
https://ai.yanxishe.com/page/TextTranslation/1321
AI研习社每日更新精彩内容,观看更多精彩内容:
深度学习的NLP工具
五个很厉害的 CNN 架构
一文带你读懂计算机视觉
Python高级技巧:用一行代码减少一半内存占用
等你来译:
(Python)3D人脸处理工具face3d
25个能放到数据湖中的语音研究数据集
如何在数据科学面试中脱颖而出
Apache Spark SQL以及DataFrame的基本概念,架构以及使用案例
【AI求职百题斩】已经悄咪咪上线啦,还不赶紧来答题?!

想知道正确答案?
回公众号聊天界面并发送“1217挑战”即可获取!
点击 阅读原文 查看本文更多内容↙