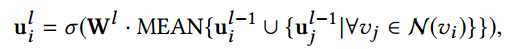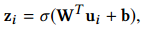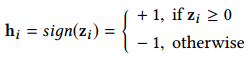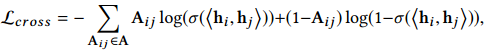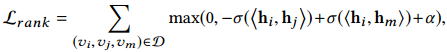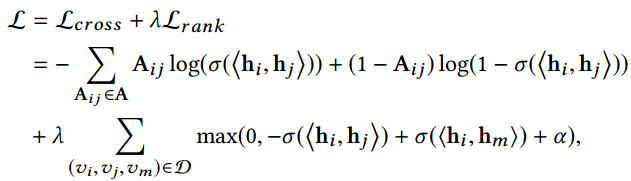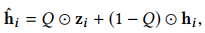WWW2020 | 基于GNN和哈希学习的高效推荐系统

2020 年 8 月 28 日 机器学习与推荐算法

嘿，记得给“ 机器学习与推荐算法 ”添加 星标

最近看了篇利用哈希技术来提高基于图神经网络的推荐系统检索速度的文章。该文的亮点本人认为主要有以下两点：（1）模型同时学习用户/物品的实值表示和离散表示，用于协调模型的效率和性能，（2）该文提出了一个端到端的训练框架，解决了哈希模型在反向传播中遇到的优化困境：即模型中包含非光滑函数sign(.)。因此把这篇文章推荐给大家。

标题：Learning to Hash with Graph Neural Networks for Recommender Systems

来源：WWW 2020

链接：https://arxiv.org/abs/2003.01917

1 Motivation

推荐系统已成为我们日常生活中支持各种在线服务的基本工具，比如网络搜索和电子商务平台。给定一个query，我们期望推荐引擎返回一小部分用户感兴趣的物品集合。这一过程中，包含了Recall和Ranking两个重要阶段。Recall主要是为了从大量（百万级）的物品中高效的检索出少量（几百几十）个候选物品；Ranking负责利用预测排序模型为用户生成一个精确的排序列表。为了提升召回质量，网络嵌入模型已经被广泛应用于推荐场景。在众多网络嵌入模型中，图神经网络（GNN）[1]作为结构化神经网络的一种特殊实例，在信息检索领域取得了最优性能。尽管如此，但在连续空间中筛选出这样一部分候选物品的计算成本太高，线性搜索的计算复杂度为，其中为物品总数，为特征维数。当较大（百万级）时，这样的复杂度仍使得模型效率低下。因此，在实际的推荐中，如何提高召回阶段的效率成为了一个亟需解决的问题。

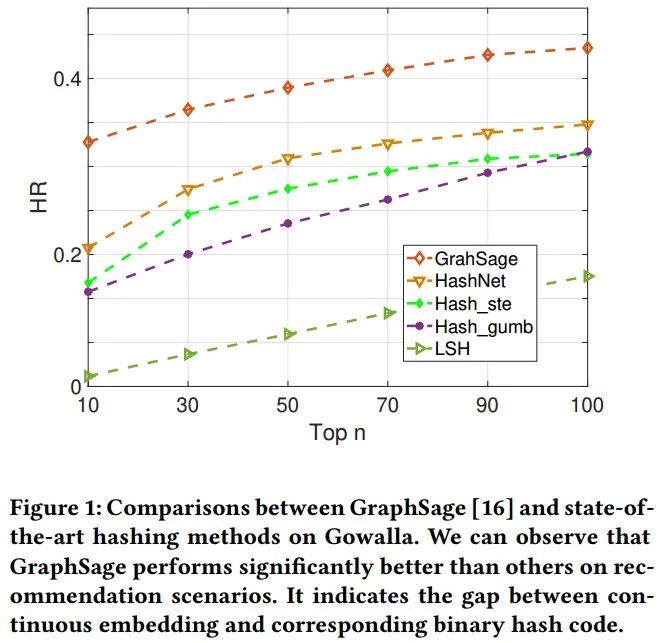
哈希技术[2]由于其从大数据中检索的高效性而引起了越来越多的关注。最近基于手工特征的哈希模型和深度哈希模型被相继提出，但前者需要首先学习实值表示，然后在后续步骤中利用符号阈值函数将其二进制化为哈希码，这样一种机制可能无法学得紧凑的二进制码，导致次优解；后者主要用于生成高质量二进制代码，与之相关联的实值嵌入的代表性能力可能很差，如图1所示。

从图1中我们发现，在推荐场景下哈希方法的推荐精度差于利用相应的实值嵌入的检索精度。因此在Ranking阶段，利用哈希方法获得的推荐精度并不是最优。

综上，为了同时解决召回效率和排序精度两大问题，论文提出了一种用于哈希图数据的新型端到端学习框架，名为HashGNN。

2 HashGNN Model

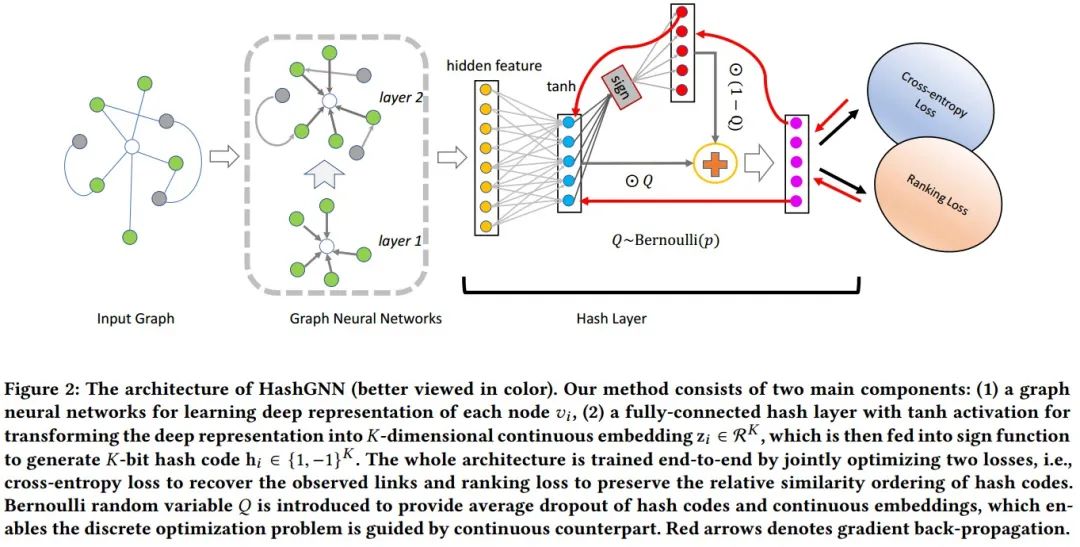
模型的整体框架如图2所示，HashGNN模型包含了两个主要部件：（1）Graph Neural Network （2）Hash Layer。模型的大致流程为：将graph作为输入，通过一个图编码器生成一个节点的中间表示，再将中间表示喂入哈希层从而学得节点的哈希码。

在介绍各部件之前，我们先给出相关定义：

2.1 Graph Encoder

在该工作中，作者选择一个两层的图卷积网络（graph convolutional network, GCN）[3]作为图编码器。在GCN中生成嵌入的主要步骤为整合节点的邻居信息。令为深度为l的层上的节点的表示，则

其中为第l层上的权重矩阵，MEAN为平均聚合器，为节点的邻居集合。

2.2 Hash Code Embedding

在获得了节点的中间表示后，将节点的中间表示输入到一个全连的哈希层，将中间表示按如下所示转换为维的嵌入向量：

其中为参数矩阵，为偏置向量，为函数。为了生成最终的哈希码，利用符号函数将连续的维实值向量转换为二进制码，

为了能够更好地在海明空间中保存图的拓扑信息，我们利用交叉熵损失来重构观测到的连接：

2.3 Ranking Preserving Hash Coding

尽管帮助模型保存了图的结构信息，使得相似的节点有着相似的表示，但是，在推荐场景中，候选物品的相关排序也是十分重要的。基于此，论文提出保存节点在海明空间内的相对排序，并提出了一种排序结构增强损失函数：

其中三元组表示相较于，与更相似，为三元组的集合，是用来控制相似与不相似哈希码之间差异的边缘参数。

3 End-to-End Learning of Hash Code

结合上述讨论的因素，总体的损失函数表述为：

其中为用来平衡交叉熵损失和排序损失重要的参数。

由于模型中存在非光滑的函数，模型无法通过标准的随机梯度下降（Stochastic Gradient Descent, SGD）方法来进行优化。

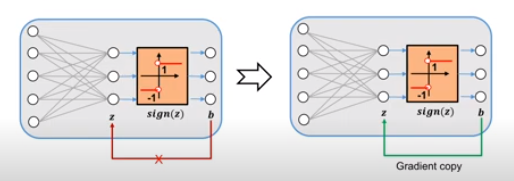
为了能够端到端的优化HashGNN模型，论文近似估算直通估算器STE的梯度[4]，即在前向传播中，使用函数生成哈希码，然后在反向传播中，将梯度从直接复制到，通过这样一种优化机制，便可以利用梯度下降算法来优化哈希模型。由于STE方法经历梯度放大问题，从而导致模型训练不稳定和次优解，为了解决这一问题，作者提出在模型训练过程中将实值嵌入向量联系起来，因此，作者利用实值向量和哈希码的dropout平均来替代二进制码进行训练，

其中表示带有参数的伯努利分布。

4 Experiments

论文针对以下四个问题展开了实验：

4.1 Q1

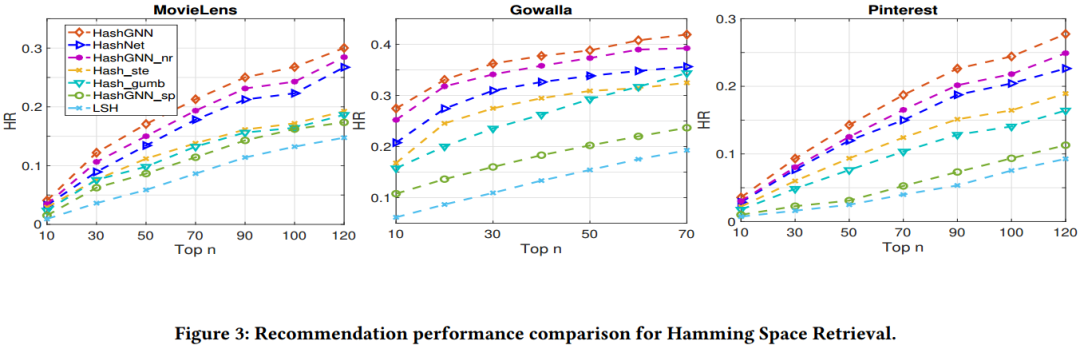
这一节中，我们通过海明空间检索来对比各个模型的性能。实验结果如图3所示。

观察上述结果发现，本文方法一直优于其他模型。

4.2 Q2

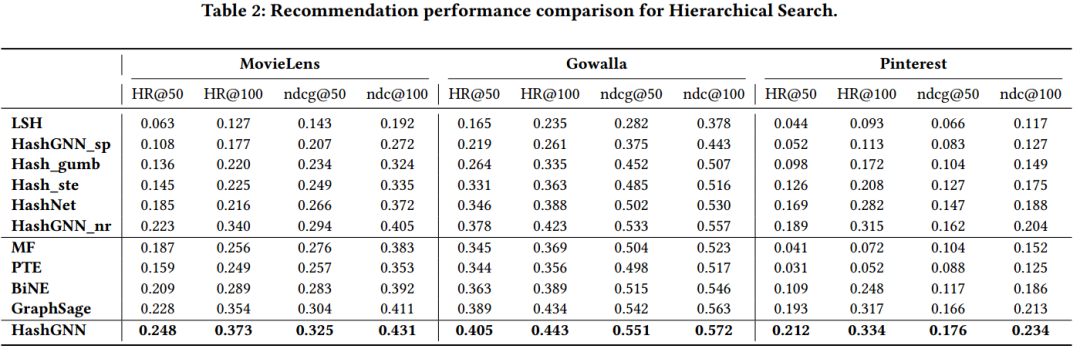
在本节中，作者试图了解通过哈希方法和连续网络嵌入方法学习到的节点嵌入的表示能力，并在阶级搜索设置下进行了实验。与海明空间搜索不同，阶级搜索需要同时利用哈希码和实值嵌入进行预测，即首先利用海明空间检索返回一部分候选物品集，再利用候选物品的实值嵌入进行排序指导最后的推荐。因此，阶级搜索衡量了哈希模型生成二进制码和实值嵌入的能力。

观察可知，HashGNN在众多模型中获得了最优异的性能。同时观察图3和表2，发现在阶级搜索的场景下，所有模型的性能都优于在海明空间检索的性能。这说明，相较于实值嵌入，哈希码精确的检索能力有限。

4.3 Q3

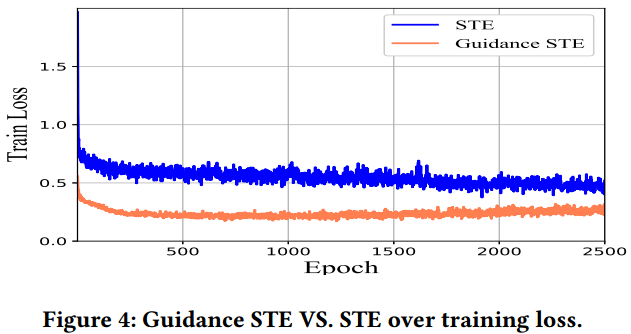
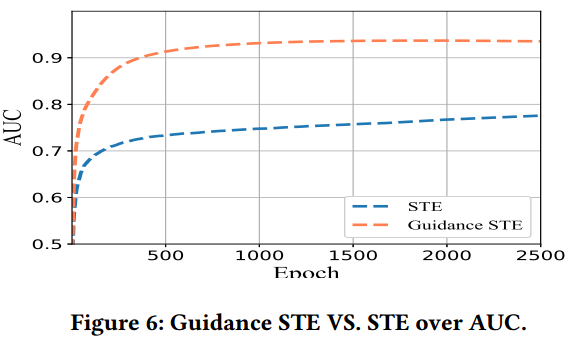
在这一节中作者对比了改进后的STE算法相较于原始的STE算法有何优势。

观察发现，不论是训练损失还是AUC，改进后的STE总是优于原始STE。

4.4 Q4

在这一节中，作者研究了不同参数对于模型性能的影响。

（由于参数实验过多，这里便不一一说明，更多细节可阅读原文）

小结

在这项工作中，作者使用图神经网络研究无监督深度哈希的问题，以进行推荐。提出了一个新的HashGNN框架，该框架以端到端的方式同时学习深度哈希函数和图表示。该模型较灵活，可以用于扩展现有的各种图神经网络。通过共同优化两个损失，即重建损失以重建观察到的连接以及排序损失用以保留哈希码的相对相似性排名，来训练整个架构。为了使梯度能够在反向传播中传播，作者提出了一种基于实值嵌入指导的STE得到了一种新颖的离散优化策略。实验表明所提离散优化策略不仅加速了训练过程同时还提升了模型性能。

参考文献

[1] Wenqi Fan, Yao Ma, Qing Li, Yuan He, Eric Zhao, Jiliang Tang, and Dawei Yin. 2019. Graph Neural Networks for Social Recommendation. arXiv preprint arXiv:1902.07243 (2019).

[2] Jun Wang, Wei Liu, Sanjiv Kumar, and Shih-Fu Chang. 2015. Learning to hash for indexing big dataâĂŤA survey. Proc. IEEE 104, 1 (2015), 34–57.

[3] Will Hamilton, Zhitao Ying, and Jure Leskovec. 2017. Inductive representation learning on large graphs. In NIPS. 1024–1034.

[4] Yoshua Bengio, Nicholas Léonard, and Aaron Courville. 2013. Estimating or propagating gradients through stochastic neurons for conditional computation. arXiv preprint arXiv:1308.3432 (2013).