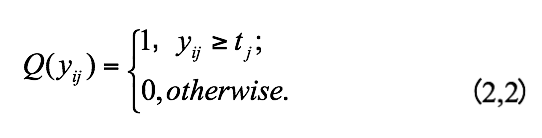AI综述专栏| 大数据近似最近邻搜索哈希方法综述(上)(附PDF下载)
AI综述专栏
在科学研究中,从方法论上来讲,都应先见森林,再见树木。当前,人工智能科技迅猛发展,万木争荣,更应系统梳理脉络。为此,我们特别精选国内外优秀的综述论文,开辟“综述”专栏,敬请关注。
导读
最近邻搜索(Nearest Neighbor Search)也称作最近点搜索,是指在一个尺度空间中搜索与查询点最近点的优化问题。最近邻搜索在很多领域中都有广泛应用,如:计算机视觉、信息检索、数据挖掘、机器学习,大规模学习等。其中在计算机视觉领域中应用最广,如:计算机图形学、图像检索、复本检索、物体识别、场景识别、场景分类、姿势评估,特征匹配等。由于哈希方法可以在保证正确率的前提下减少检索时间,如今哈希编码被广泛应用在各个领域。本文是关于大数据近似最近邻搜索问题中应用哈希方法的综述。文章分为两部分,本篇为第一部分。
「关注本公众号,回复"曹媛",获取完整版PPT」
该文是曹媛博士论文的一部分,谢绝拷贝,违者必究
作者简介
作者曹媛,大连理工大学计算机科学与技术专业在读博士,研究领域:机器学习,大数据检索,哈希算法。
目 录
1 简介1
1.1 背景1
1.2 基于哈希的近似最近邻搜索框架2
2 哈希编码方法简介5
2.1 哈希机理特性6
2.1.1 数据依赖性6
2.1.2 哈希过程7
2.1.2.1 传统哈希方法7
2.1.2.2 基于深度学习的哈希方法9
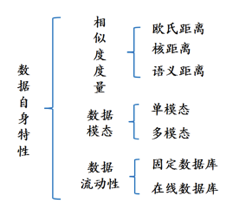
2.2 数据自身特性 10
2.2.1 相似度度量10
2.2.1.1 欧氏距离10
2.2.1.2 核距离10
2.2.1.3 语义距离10
2.2.2 数据模态11
2.2.2.1 单模态11
2.2.2.2 多模态11
2.2.3 数据流动性11
2.2.3.1 固定数据库11
2.2.3.2 在线数据库11
2.3 哈希平台12
2.3.1 单机12
2.3.2 分布式12
3 哈希排序方法简介12
3.1 加权汉明距离13
3.1.1 按位算权重13
3.1.2 按类别算权重13
3.2 非对称距离14
4 总结15
参考文献15
1 简介
1.1 背景
最近邻搜索(Nearest Neighbor Search)也称作最近点搜索,是指在一个尺度空间中搜索与查询点最近点的优化问题。具体定义如下:在尺度空间M中给定一个数据库点集S和一个查询点q ∈ M,在S中找到距离q最近的点。其中M为多维的欧几里得空间,距离由欧几里得距离决定。最近邻搜索在很多领域中都有广泛应用,如:计算机视觉、信息检索、数据挖掘、机器学习,大规模学习等。其中在计算机视觉领域中应用最广,如:计算机图形学、图像检索、复本检索、物体识别、场景识别、场景分类、姿势评估,特征匹配等。
随着互联网和电子技术的高速发展,网络上信息量的增长异常迅速,每秒钟都会上传大量的文本,图像等信息。这给很多需要进行高效最近邻搜索的领域带来了极大的挑战。当数据库中的信息量较少的时候,我们可以使用最简单有效的穷尽搜索方式,即:将数据库中的点与查询点一一比较欧式距离,最终根据距离的大小排序。时间复杂度为线性复杂度 ,
和
分别是数据的维度和样本数。但当数据库的规模庞大,如有上百万到上亿个点时,线性搜索的方式已不适用。另外,如在计算机视觉领域,已越来越倾向使用高维度数据或结构化数据来更加精确地表达图像信息,并使用复杂的相似度公式计算图像间距离,在这些情况下,穷尽搜索的方式无法高效完成最近邻搜索。
因此,人们开始使用近似最近邻搜索(Approximate Nearest Neighbor Search)方法快速搜索有效解,其定义为: 。其中,
为查询点,
为精确解,
为近似误差,
为某种距离函数。早期被大量使用的是通过各种树形结构对特征空间分割的方式,最经典的以K-D树为代表。不过,虽然这些利用树形结构做近似最近邻搜索的方法在处理低维数据的时候有较好的性能,但随着数据维度的增长,该类方法的时间性能显著降低,有时甚至比线性搜索还差。
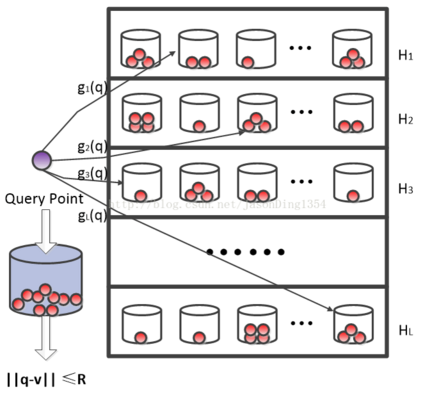
后来就不断有人提出各种基于哈希编码的近似最近邻搜索方法。哈希编码即将数据库中的点(高维向量)通过编码的方式转化为二进制向量,同时尽可能保持原始空间中点之间的距离关系。查询过程一般分为三步:
a、计算查询点的二进制编码;
b、找到与查询点具有相同二进制码的哈希篮子;
c、将该哈希篮子中的所有点导入内存并根据要求对它们重新排序。
哈希编码主要有两大优点:
a、空间复杂度低。原始空间中的点一般为几百到几千维,每一维都是实数值(占多位二进制),而哈希码为二进制向量,维度大概只有几十到几百维;
b、时间复杂度低。哈希码之间的距离用汉明距离计算,在计算机中仅仅为一个异或操作的时间复杂度。同时,由于哈希码占有较少的空间,可以更多地存入内存,因而在计算时减少CPU访问外存的次数,从而减少时间复杂度。
当然,哈希编码的最大缺点就是损失了大量原始信息从而降低检索精度。因此,自哈希编码提出以来,人们不断探寻可以提高哈希编码精度的方法。但Antonio Torralba等人早在2008年就提出:以图像压缩为例,我们可以使用少量位数表示图像信息而不影响图像识别的准确率(如图1.1)。因此,哈希方法是可以在保证正确率的前提下减少检索时间的,如今哈希编码被广泛应用在各个领域。
图1.1 图像压缩示例
1.2 基于哈希的近似最近邻搜索框架
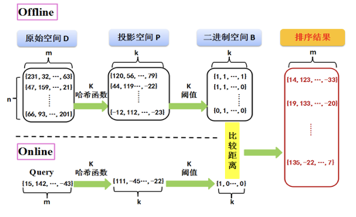
图1.2描述了一种典型的基于阈值哈希的近似最近邻搜索框架。如图所示,原始空间D中有 n 个 m 维的向量,这些向量可来自于各种应用领域,如图像、文本、生物医学等。当 n 与 m 的数值较大时( n 达到百万至亿数量级,m 达到几千维以上),我们使用哈希方法可以有效解决大规模近似最近邻搜索问题。由于基于阈值的哈希方法是最常用的哈希编码方法,因此我们以其为例阐述近似最近邻搜索的完整过程。
基于哈希的近似最近邻搜索过程主要分为两阶段:Offline和Online。图中虚线上面为Offline阶段,即对数据库中点进行与查询点无关的哈希编码。该过程可分为两步:首先使用 k 个哈希函数将原始空间 D 中 n 个 m 维的点映射到 k 维的投影空间 P 中,该映射要尽可能保持原始空间中点间的相似度关系。然后再使用 k 个阈值将投影空间中的点映射到二进制空间 B 中,即将其每一维度映射为“0”或“1”,阈值的选择要满足哈希特性(如平衡性);图中虚线下面为Online阶段,即对查询点哈希编码。对于查询点,我们使用与Offline阶段中同样的哈希函数与阈值,将 m 维查询点编码为 k 维二进制。最后,通过比较查询点二进制码和数据库中点二进制码之间的汉明距离即可将数据库中的点按照汉明距离由小到大排序。
图1.2 哈希近似最近邻搜索框架
下面我们从不同的角度将哈希方法分类。首先哈希方法可以分为两大类:哈希编码和哈希排序。哈希编码又可以从三个角度分类:哈希机理特性,数据自身特性,哈希平台。哈希排序可以分为两类:加权汉明距离和非对称距离。具体分类细节如图1.3所示。
图1.3 哈希方法分类
2 哈希编码方法简介
哈希编码即将数据库中的点(高维向量)通过编码的方式转化为二进制向量,同时尽可能保持原始空间中点之间的距离关系。将其符号化为:数据库矩阵 ,其中每个行向量代表一个 m 维的点,共 n 个点。哈希编码就是采用某种映射的方式将矩阵 D 映射为二进制矩阵
,矩阵中每个值为二进制0或1,k 为二进制的码长。对于查询点
,采用同样的哈希编码方法将其映射为
。
与
之间的汉明距离为:
。在查询时,对数据库 D 中的 n 个点按
由小到大排序。
哈希编码必须满足的要求主要有以下三个:
a、码长短。因为我们要将大量的信息存入到内存中,如:普通的工作站有16GB的内存,若存储250百万幅图像,每幅图像最多可以用64位二进制表示;
b、保距。即原始空间中相似(任意相似度:欧氏距离、核距离、语义相似度等)的点编码后二进制编码间的汉明距离要短;
c、效率高。即无论是在训练时学习哈希编码的参数,还是对新的输入点编码,速度都要快。
为了得到更加高效的哈希码,哈希编码一般还需要满足以下两个特性:平衡性和独立性。
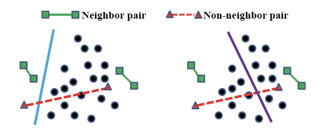
a、平衡性:即编码后的所有点的每一维度都有一半编码为0,一半编码为1。当编码达到平衡时,熵达到最大,信息量最大,哈希编码最好。如图1.4所示,左右两幅图的哈希方法都可以使带有标签的点对正确编码,但很明显右侧图哈希的空间分割有较大的熵,包含更大的信息量,因此比左侧图哈希好。
图1.4 哈希平衡性
b、独立性:即不同哈希函数之间相互独立。各个哈希函数若不相互独立则会产生类似的哈希结果,造成信息冗余,因此相互独立的哈希函数才可以对数据空间进行最有效的分割。
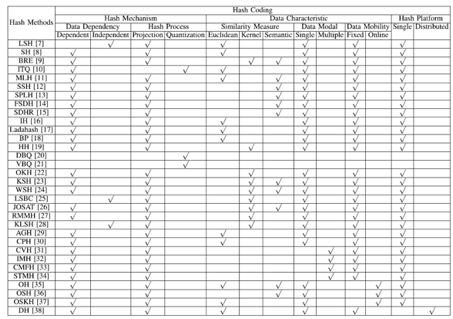
常见哈希编码方法的分类如表2.1所示,其中标号为[1]中参考文献。
2.1 哈希机理特性
2.1.1 数据依赖性
如图1.2所示,哈希编码的第一步是学习 k 个哈希函数将原始空间 D 中 n 个 m 维的点映射到 k 维的投影空间 P 中。早期哈希函数的学习是不依赖于数据分布的,如Locality-Sensitive Hashing (LSH) ,哈希函数是从符合高斯分布的数据中随机选取的若干个投影分布。尽管随着投影分布数量的增加,LSH搜索结果渐近逼近理论值,但是为了获得满意的精度往往需要较长的码长和较多的哈希表。由于时间空间的限制很难扩展到上百万的数据集上。因此,依赖于数据分布的哈希方法被不断提出。早期经典的依赖于
表2.1 哈希编码方法分类
数据分布学习哈希函数的哈希方法以Spectral Hashing (SH) 为代表,SH在数据库数据集上构造了一个目标函数保持原始空间和汉明空间之间的相似度表示,即原始空间中相似的数据点要投影到汉明空间中相似的二进制码上。再加上上面提到的独立性和平衡性限制,最小化SH目标函数得到的数据库二进制码的解即为:其拉普拉斯矩阵的前 k 个最小特征值(除了0)所对应的 k 个特征向量。
尽管SH与LSH相比由于利用到了数据分布信息往往可以表示出较高的精度,但SH有以下三个缺点:1) SH由于没有学习明确的哈希函数使得无法将其直接应用到新输入的数据点上;2) SH没有明确的理论依据,即随着码长的增加,哈希码之间的汉明距离是否会收敛于原始空间的相似度表示是不明确的;3) 在实际应用中,投影后的数据点的信息往往只分布在前几个维度上,导致SH 只在较短码长的二进制码上性能较好。在下一节的哈希过程中,我们会详细描述SH的哈希函数和哈希码学习过程。
2.1.2 哈希过程
2.1.2.1 传统哈希方法
在2014年以前,大多数哈希方法都依赖于传统的两步走哈希框架:投影和量化。在投影阶段,使用 k 个哈希函数将原始空间 D 中 n 个 m 维的点映射到 k 维的投影空间 P 中,该映射要尽可能保持原始空间中点间的相似度关系。在量化阶段,使用 k 个阈值将投影空间中的点映射到二进制空间 B 中,即将其每一维度映射为“0”或“1”。
下面我们用矩阵运算的形式表示投影量化两阶段过程。假设原始空间中的数据点表示为 ,组成的数据库矩阵为
。哈希方法的目标即找到一个投影矩阵
,其中 c 表示二进制码长度。对于
,哈希函数定义为:
其中 是矩阵 P 的一列,
是数据库点对应的二进制码矩阵,同时
其中, 是由哈希方法确定的第 j 位阈值。由此,哈希编码的整个过程可以表示为:B=Q(XW) 。从(2,1) 中,我们可以看出一个哈希函数可以将数据点投影为一位,如果想要获得 k 位哈希码,我们需要 k 个哈希函数。各个传统哈希方法之间的区别主要在于投影矩阵 W 的计算上。下面我们举例分析哈希方法是如何学习投影矩阵以及如何量化投影空间中的数据点的。
1.投影
我们将投影过程定义为 P=XW。目前大多数传统哈希方法通过构造目标函数学习哈希函数,最大化或最小化目标函数可以保持原始空间和汉明空间中点之间的相似度表示。同时为了进一步提高哈希函数的性能,还需要满足一些限制,如:平衡性和独立性。
下面我们以SH为例分析哈希方法的投影过程,以下是SH的目标函数和限制条件:
minimize:
subject to:
其中, 和
分别表示点 i 和点 j 在投影空间中的第 l 位。
表示点 i 和点 j 在原始空间中的相似度。观察发现,在原始空间中如果两个点很相似,则
值较大,那么
应当较小。因此,SH通过最小化目标函数同时满足平衡和独立两限制条件(2,3) 学习哈希函数。
2.量化
在量化阶段,投影空间中的点通过阈值量化为二进制码。目前大多数哈希方法将每个投影维度用一个阈值量化,被称作单位量化。阈值通常由平衡性限制( )求得。然而单位量化一个比较严重的缺点是其阈值往往分布在数据密度最高的区域,这将导致很多邻近的数据点被量化为完全不同的二进制码。因此,双位量化被提出。双位量化即对每个投影维度动态学习两个阈值并将其编码为两位二进制码(01,00,10)。阈值的学习使其避免设置在数据点密集的区域。除此之外,由于一些哈希函数可能比另一些携带更多的信息,变位量化被提出为每个哈希超平面分配变化位数的哈希码。变位量化首先构造一个目标函数使得为那些更好保持数据在原始空间中相似度关系的维度分配更多的哈希位。与单位量化和双位量化相比,变位量化可以获得更高的精度。
2.1.2.2 基于深度学习的哈希方法
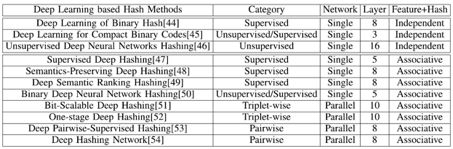
对于图像检索应用中的哈希方法,输入的图像往往由人工视觉特征向量表示。这些人工视觉特征向量并不能严格保持图像对之间的精确语义相似度信息,这将导致学习的哈希函数性能较低。因此,基于深度学习的哈希方法被不断提出。这类方法的不同主要体现在四个方面:
1.监督性
监督性即在使用深度神经网络框架学习哈希码的过程中是否利用到原始图像的标签或相似点对信息,分为监督和非监督。对于监督的基于深度学习的哈希方法,除了传统的依赖于图像标签信息的监督哈希方法,另一些利用相似对信息的监督哈希方法又可以分为两类,一类依赖于成对相似度信息,另一类依赖于三元组相似度信息。
2.网络并行性
即只使用单一的深度神经网络还是并行使用多个深度神经网络学习哈希码。
3.网络层数
即使用的深度神经网络的层数。
4.独立性
即从图像中学习特征表示和哈希编码两个过程是联合学习的还是独立学习的。
对当前几种经典的基于深度学习哈希方法的分类细节详见表2.2,其中标号为[1]中参考文献。
表2.2 基于深度学习哈希方法分类
历史文章推荐:
AI综述专栏 | 脑启发的视觉计算2017年度关键进展回顾(附PPT)
AI综述专栏 | 11页长文综述国内近三年模式分类研究现状(完整版附PDF)
AI综述专栏 | 朱松纯教授浅谈人工智能:现状、任务、构架与统一(附PPT)
【AIDL专栏】罗杰波: Computer Vision ++: The Next Step Towards Big AI