征文 | 数学与乐趣

2019 年 7 月 16 日 遇见数学

本文参与遇见数学＃数学蒲公英＃第2次征文活动，作者戴玥旻，上海师范大学附属中学高一4班学生。

谈论到数学，许多人的第一反应就是初等数论，解析数论，代数学，微分代数，几何学，拓扑学等等这种常人认为枯燥乏味，没有什么乐趣的东西。但是事实上，许多的数学家包括物理学家，化学家在内，本人都是非常风趣。比如说勒内·托姆，他是法国人，35岁得的菲尔兹奖。

勒内·托姆，突变论的创始人，于1958年获菲尔兹奖。(图自维基)

在一次采访当中，作为数学家的托姆同两位古人类学家讨论问题。谈到远古的人们为什么要保存火种时，一个人类学家说，因为保存火种可以取暖御寒;另外一个人类学家说，因为保存火种可以烧出鲜美的肉食。而托姆说，因为夜幕来临之际，火光摇曳妩媚，灿烂多姿，是最美最美的。美丽是我们的数学家英雄们永恒的追求。看，数学家不仅仅只追求数学，更是追求美丽。

当然数学家们也并不仅仅关注于美丽的事物，生活中的任何不一样的事物都会引起他们的观察，不一样的想法。正如世界近代三大数学难题之一的四色定理(four color theorem)，事实上应该被称为四色猜想。困扰了人类多少年，多少数学家钻研其中却又无法证明。只能靠计算机验证目前的地图四色就够了。四色定理证明的关键可以归纳为二维平面内两条直线相交的问题。

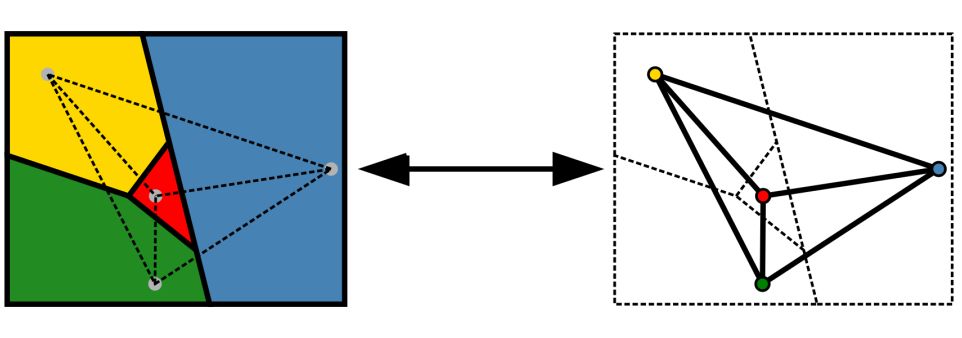
一个四个国家的地图转化为一个平面图(图自维基)

1.将地图上不同的区域用不同的点来表示。
2.点与点之间的连线用来表示地图上两区域之间的相邻逻辑关系，所以, 线与线之间不可交叉（即不可存在交叉而没有公共交点的情况），否则就超越了二维平面，而这种平面暂时称它为逻辑平面，它只反应区域之间的关系，并不反应实际位置。

通过以上的变换处理，可以将对无穷尽的实际位置的讨论，变为有条理可归纳的逻辑关系的讨论，从而提供了简单书面证明的可行性。

如果证明可以用一句话来说，那就是：“二维平面不存在交叉直线，只存在共点直线”。

看起来只是简简单单的一句话，却怎么也证明不出，反倒是在类似面包圈上的形状，轻易证明出了只需要用 7 种颜色。这就像我们平时遇到数学难题时，明明感觉它就是对的，也难以举出反例，却怎么也想不出如何证明。

而这也就是数学的乐趣所在，也就是为什么如此多数学家对“它”执念这么深。当然，也不是所有的数学都需要证明，如果这样的话，那么未必太过于繁琐，对难的问题的证明也会太过于复杂，造成不必要的麻烦。

“证明一个理论在一个系统中已为实践所反复证明而被认为无须再证明的真理。如“等量加等量, 其和相等”，就是公理。”

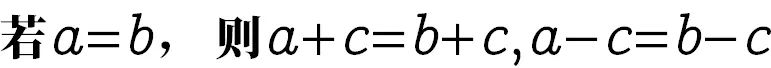
公理的出现与使用大大方便了数学的证明。自此数学也渐渐发展迅速起来，甚至被数学家称为科学的皇后。在一次“纯粹数学和应用数学联席会议”上，有人邀请希尔伯特作一次公开演讲，他这样说：“经常听到有人说，纯粹数学和应用数学是相互对立的，这是不符合事实的，纯粹数学和应用数学不是相互对立的，它们过去不曾对立过，将来也不会对立，他们是对立不起来的，因为在事实上他们两毫无共同之处。”

而我认为，这两者是相辅相成的。在现代，数学不仅作为一个解决问题的工具，而且已成为时代文化的一个重要组成部分，一些数学概念、语言已渗透到日常生活中去，一些数学原理已成为人们必备知识，如面积、体积、对称、比例、角度等成为社会生活中常见名词；比如人口增长率、生产统计图、股票趋势图等不断出现在报刊、电视等大众信息传播媒介中；而像储蓄、债券、保险、面积、体积计算（估算）、购物决策等成为人们难以回避的现实问题。那么将来的公民——现在的学生，必须具备一个解决实际应用问题的数学素养，这一切都呼唤应用问题呈现于数学教育教学过程中。

中国古代数学一向有实用的传统，数学教学中重视数学应用也并非新问题。在小学里，数学应用问题是教学的重点和难点，从未有人持异议。到了初中，学了平面几何，数学品味趋于抽象，逻辑推理不断加强，数学应用渐有淡出之势。不过，数学应用并未绝迹，诸如浓度问题、行程问题等仍有出现，平行四边形与铁栅门的关系等也总要提及。甚至我在初中学了这么多几何后仍然比较喜爱代数，以及数学应用。

一到高中，情况变得越发严重。数学一直是中学的主干课程，为什么要学那么多的数学？一般认为，数学是“能力筛子”、“思想的体操”，无非是“升学需要”、“思想健身”而已。至于有什么用，对不起，你只管学就好了。数学仿佛已经不再只为兴趣而学，之前在日记上兴冲冲写下“果然只有做数学能带给我快乐啊”的小孩已经不见了，取而代之的是一个对数学提不起兴趣，却还不得不每天面对它的大人。之前我一时兴起，对着我家的人工智能盒子问了一句，人类会灭亡吗？它只是回答了我一句：

“科技在进化，人类在退化。”

我思考了很久，退化究竟指的是什么呢？大概就是指的这样吧。

END