作者:刘宁
编辑:好困
【新智元导读】「彩票假说」指出神经网络可能存在准确率和原始网络相近的子网络。然而,这种中奖特性在许多情况中很难被观测到。最近,王言治教团队发现并揭示了中奖特性的潜在条件和基本原理。
在深度模型压缩领域中,「彩票假说」(Lottery Tickets Hypothesis)指出一个原始神经网络可能存在中奖彩票的子网络(Winning ticket),该子网络可以达到和原始网络相近的准确率。
然而,这种中奖特性(Winning property)在许多情况中很难被观测到。例如,在训练网络过程中,当使用有利于训练的相对较大的学习率时,就很难发现中奖彩票。
近期,由美国东北大学王言治教授研究组与合作组通过对「彩票假说」工作的研究,发现并揭示了中奖特性的潜在条件和基本原理。
![]()
论文链接:https://arxiv.org/pdf/2102.11068.pdf
会议论文链接:http://proceedings.mlr.press/v139/liu21aa.html
该研究发现其本质原因,即当学习率不够大时,初始化权重和最终训练权重之间存在相关性。
因此,中奖特性的存在与神经网络(Deep neural network,DNN)预训练不足有关,并且该特性不太可能发生在训练良好的神经网络中。
为了克服这个限制,该研究提出了「剪枝与微调」的方案,其在相同的剪枝算法和训练时长下始终优于中奖彩票训练的精度。
该研究对不同数据集上的多个深度模型(VGG、ResNet、MobileNet-v2)进行了广泛的实验,以证明所提出方案的有效性。目前,该文章已经被ICML 2021会议收录。
神经网络的权重剪枝技术已经被广泛研究和使用,权重剪枝可以有效地去除过度参数化的神经网络中的冗余权重,同时保持网络准确率。
典型的剪枝流程有三个主要阶段。
训练一个拥有过度参数的原始DNN;
剪枝掉原始DNN中不重要的权重;
微调剪枝后的DNN从而恢复准确率。
目前,很多工作都在研究权重剪枝领域的原理与方法。其中有代表性的「彩票假说」[1]工作中表明,在一个使用随机初始化权重的密集网络中,存在一个小的稀疏子网络,当使用与原始密集网络相同的初始权重单独训练这个稀疏子网络时,可以达到与密集网络相似的性能。
这样一个具有初始权重的稀疏子网络被称为中奖网络(Winning ticket)。中奖网络拥有如下特性:
-
训练相同随机初始化稀疏子网络
![]() T轮(或更少)将达到与密集预训练网络
T轮(或更少)将达到与密集预训练网络![]() 相似的准确率。
相似的准确率。
-
训练相同随机初始化稀疏子网络
![]() T轮和训练重新随机初始化稀疏子网络之间
T轮和训练重新随机初始化稀疏子网络之间![]() 应该有明显的准确率差距,前者应更高。
应该有明显的准确率差距,前者应更高。
在彩票假说工作中发现,在低学习率的情况下可以通过迭代剪枝算法(Iterative pruning)观察到中奖特性,但在较高的初始学习率下,特别是在较深的神经网络中,很难观察到。
例如,在初始学习率低至0.0001情况下,「彩票假说」工作在CIFAR-10数据集上的CONV-2/4/6架构确定了中奖网络。
对于CIFAR-10上的ResNet-20和VGG-19等更深的网络,只有在低学习率的情况下才能识别出中奖网络。在较高的学习率下,需要额外的预热训练(Warm up epochs)来找到中奖网络。
在Liu等人的工作「Rethinking the value of pruning」[2]中,它重新审视了「彩票假说」工作,发现在广泛采用的学习率下,中奖彩票与随机重新初始化相比,并没有准确率优势。这就对中奖特性的第二个方面提出了质疑,即训练![]() 和训练
和训练
![]() 之间的精度差距。
此外,接下来Frankle等人的工作「Stabilizing the lottery ticket hypothesis」[3]提出了迭代剪枝与回倒的方式从而稳定识别中奖网络。
在本工作中,作者研究了中奖特性背后的基本条件和原理。并在各种代表性的神经网络和数据集上进行大量实验,重新审视了「彩票假说」工作,证实了
只有在低学习率下才存在中奖特性。
事实上,这样的「低学习率」已经明显偏离了标准学习率,并导致预训练的DNN的准确率明显下降。
通过引入提出的相关性指标进行定量分析,作者发现,当学习率不够大时,潜在的原因主要归因于初始化权重和最终训练的权重之间的相关性。
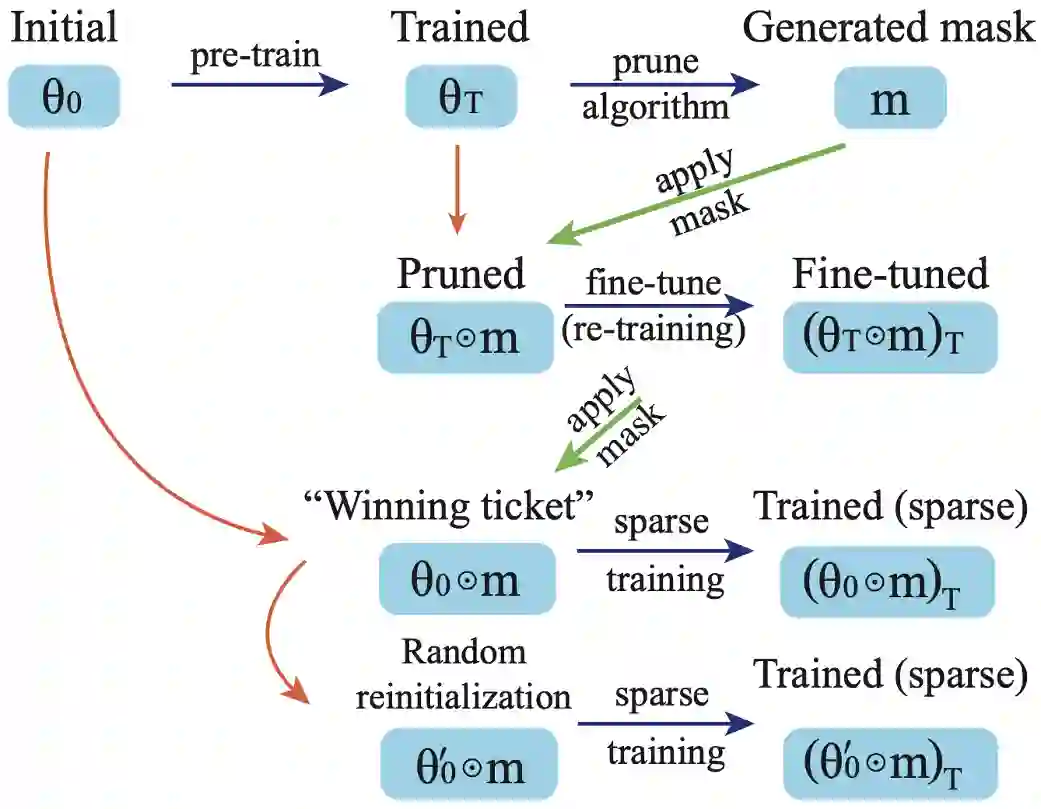
图1 不同训练阶段的表示方法示意图:包括预训练、剪枝(剪枝掩码生成)、稀疏训练以及「剪枝与微调」
本工作在各种DNN架构和CIFAR-10和CIFAR-100数据集上重新审视了「彩票假说」工作的实验,包括VGG-11、ResNet-20和MobileNet-V2。作者的目的是研究中奖特性存在的精确条件。
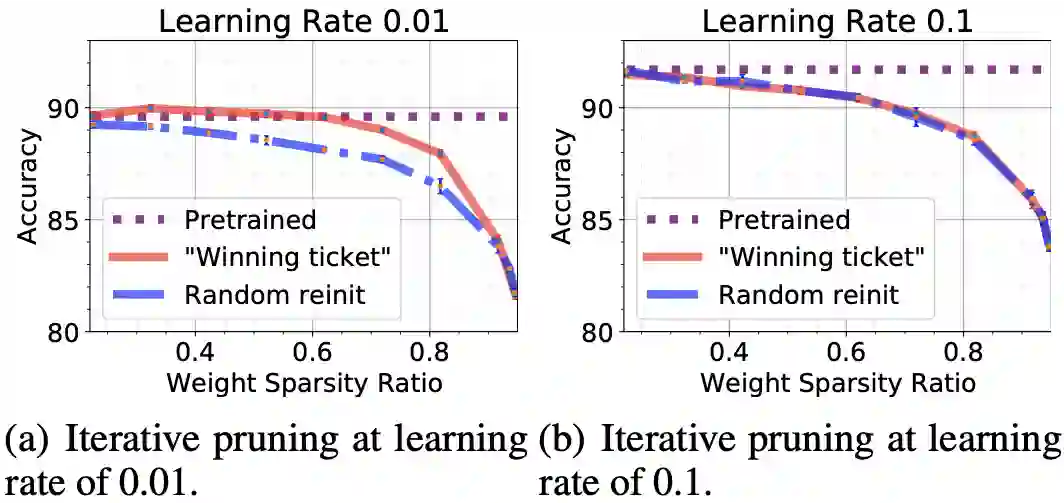
图2 CIFAR-10数据集上的ResNet-20网络在学习率为0.01和0.1时的随机重新初始化和「中奖网络」的展示
以ResNet-20的CIFAR-10数据集上为例,在初始学习率为0.01的情况下,预训练的DNN的准确率为89.62%。在不同的稀疏率下,「中奖网络」的表现持续优于随机重初始化。在稀疏率为62%时,它达到了最高的准确率90.04%(高于预训练的DNN)。
这与「彩票假说」工作在同一网络和数据集上发现的观察结果相似。
另一方面,在初始学习率为0.1的情况下,预训练的DNN的准确率为91.7%。在这种情况下,「中奖网络」的准确率与随机重新初始化相似,在有意义的稀疏率下(例如50%或以上),无法达到接近预训练的DNN的准确率。因此,没有满足中奖特性。
从这些实验来看,在低学习率的情况下,中奖特性存在,但在相对较高的学习率下很难发现,这在「Rethinking the value of pruning」[2]工作中也观察到类似现象。
然而,需要指出的是,相对较高的学习率0.1(实际上是这些数据集的标准学习率)导致预训练的DNN的准确率明显高于低学习率(91.7%对89.6%)。
在「彩票假说」的设置中,在学习率为0.1的情况下,其稀疏训练的结果(「中奖网络」,随机重新初始化)也是相对较高。
这一点在之前的相关讨论中是缺失的。
现在的关键问题是:上述两个观察结果是相关的吗?如果答案是肯定的,这意味着中奖特性对DNN来说并不普遍,也不是DNN本身或者相关应用的自然特性。相反,它表明当学习率不够大时,原始的预训练DNN没有得到很好的训练。
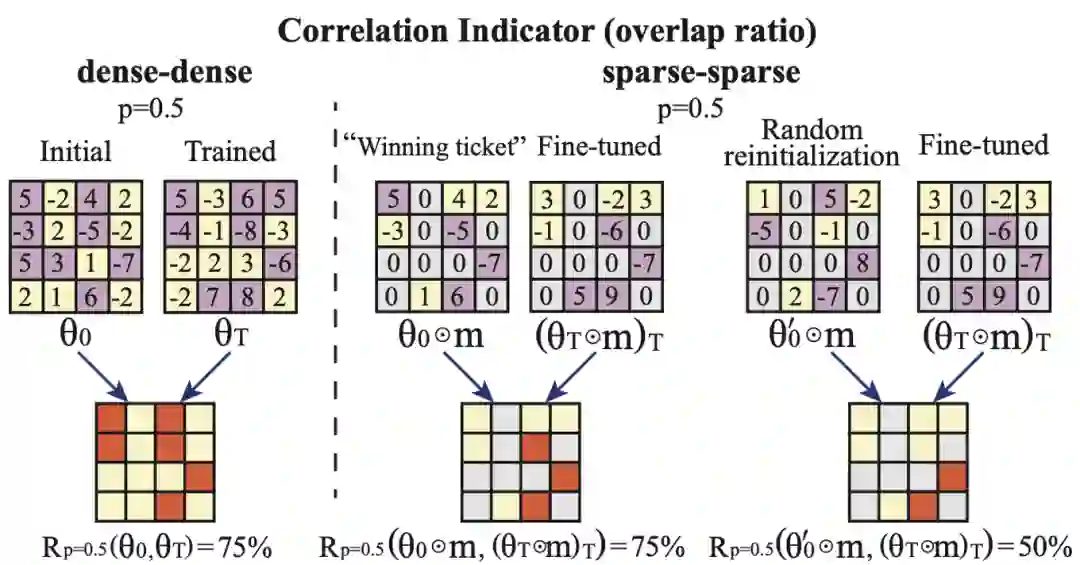
作者的假设是上述观察结果是相关的,这主要归因于当学习率不够大时,初始化的权重和最终训练的权重之间存在相关性。在验证假设之前,作者将引入一个相关性指标(correlation indicator,CI)进行定量分析。
图3 CIFAR-10上的ResNet-20在学习率为0.01和0.1时的随机重新初始化和「中奖网络」的说明
定义相关性指标用来量化两组权重
之间的精度差距。
此外,接下来Frankle等人的工作「Stabilizing the lottery ticket hypothesis」[3]提出了迭代剪枝与回倒的方式从而稳定识别中奖网络。
在本工作中,作者研究了中奖特性背后的基本条件和原理。并在各种代表性的神经网络和数据集上进行大量实验,重新审视了「彩票假说」工作,证实了
只有在低学习率下才存在中奖特性。
事实上,这样的「低学习率」已经明显偏离了标准学习率,并导致预训练的DNN的准确率明显下降。
通过引入提出的相关性指标进行定量分析,作者发现,当学习率不够大时,潜在的原因主要归因于初始化权重和最终训练的权重之间的相关性。
图1 不同训练阶段的表示方法示意图:包括预训练、剪枝(剪枝掩码生成)、稀疏训练以及「剪枝与微调」
本工作在各种DNN架构和CIFAR-10和CIFAR-100数据集上重新审视了「彩票假说」工作的实验,包括VGG-11、ResNet-20和MobileNet-V2。作者的目的是研究中奖特性存在的精确条件。
图2 CIFAR-10数据集上的ResNet-20网络在学习率为0.01和0.1时的随机重新初始化和「中奖网络」的展示
以ResNet-20的CIFAR-10数据集上为例,在初始学习率为0.01的情况下,预训练的DNN的准确率为89.62%。在不同的稀疏率下,「中奖网络」的表现持续优于随机重初始化。在稀疏率为62%时,它达到了最高的准确率90.04%(高于预训练的DNN)。
这与「彩票假说」工作在同一网络和数据集上发现的观察结果相似。
另一方面,在初始学习率为0.1的情况下,预训练的DNN的准确率为91.7%。在这种情况下,「中奖网络」的准确率与随机重新初始化相似,在有意义的稀疏率下(例如50%或以上),无法达到接近预训练的DNN的准确率。因此,没有满足中奖特性。
从这些实验来看,在低学习率的情况下,中奖特性存在,但在相对较高的学习率下很难发现,这在「Rethinking the value of pruning」[2]工作中也观察到类似现象。
然而,需要指出的是,相对较高的学习率0.1(实际上是这些数据集的标准学习率)导致预训练的DNN的准确率明显高于低学习率(91.7%对89.6%)。
在「彩票假说」的设置中,在学习率为0.1的情况下,其稀疏训练的结果(「中奖网络」,随机重新初始化)也是相对较高。
这一点在之前的相关讨论中是缺失的。
现在的关键问题是:上述两个观察结果是相关的吗?如果答案是肯定的,这意味着中奖特性对DNN来说并不普遍,也不是DNN本身或者相关应用的自然特性。相反,它表明当学习率不够大时,原始的预训练DNN没有得到很好的训练。
作者的假设是上述观察结果是相关的,这主要归因于当学习率不够大时,初始化的权重和最终训练的权重之间存在相关性。在验证假设之前,作者将引入一个相关性指标(correlation indicator,CI)进行定量分析。
图3 CIFAR-10上的ResNet-20在学习率为0.01和0.1时的随机重新初始化和「中奖网络」的说明
定义相关性指标用来量化两组权重
![]() 和
和
![]() 之间的最大幅值的部分权重的位置的重叠度。具体公式如下:
权重的相关性意味着如果一个权重的幅值在初始化时就大,那么它在训练后也是大的。
产生这种相关性的原因是学习率太低,权重更新太慢。这种权重的相关性对于神经网络训练来说是不可取的,通常会导致较低的准确率,在一个良好训练的神经网络中,权重的幅值应该更多地取决于这些权重的位置而不是初始化。
因此当权重的相关性很强时,神经网络的准确率将会变低,也就是说,没有经过良好的训练。
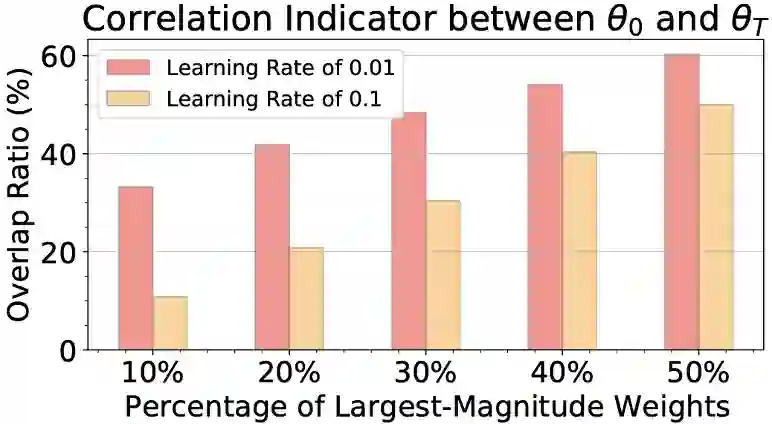
图4 在学习率为0.01和0.1时,初始权重和预训练权重之间的重叠率(当p=10%、20%、30%、40%和50%时)
为了验证上述说法,作者进行了实验,以不同的初始学习率得出神经网络预训练的相关性指标
之间的最大幅值的部分权重的位置的重叠度。具体公式如下:
权重的相关性意味着如果一个权重的幅值在初始化时就大,那么它在训练后也是大的。
产生这种相关性的原因是学习率太低,权重更新太慢。这种权重的相关性对于神经网络训练来说是不可取的,通常会导致较低的准确率,在一个良好训练的神经网络中,权重的幅值应该更多地取决于这些权重的位置而不是初始化。
因此当权重的相关性很强时,神经网络的准确率将会变低,也就是说,没有经过良好的训练。
图4 在学习率为0.01和0.1时,初始权重和预训练权重之间的重叠率(当p=10%、20%、30%、40%和50%时)
为了验证上述说法,作者进行了实验,以不同的初始学习率得出神经网络预训练的相关性指标
![]() 。
以CIFAR-10数据集上的ResNet-20为例进行说明。图4展示了在学习率分别为0.01和0.1时,初始权重
。
以CIFAR-10数据集上的ResNet-20为例进行说明。图4展示了在学习率分别为0.01和0.1时,初始权重
![]() 和来自神经网络预训练的权重的相关指标。与学习率为0.1的情况相比,学习率为0.01时相关性指标明显较高。
这一观察表明,在学习率为0.01的情况下,
和来自神经网络预训练的权重的相关指标。与学习率为0.1的情况相比,学习率为0.01时相关性指标明显较高。
这一观察表明,在学习率为0.01的情况下,![]() 的较大幅值的权重没有被完全更新,说明预训练的神经网络没有被很好地训练更新。
在学习率为0.1的情况下,权重被充分更新,因此在很大程度上不依赖于初始权重(
的较大幅值的权重没有被完全更新,说明预训练的神经网络没有被很好地训练更新。
在学习率为0.1的情况下,权重被充分更新,因此在很大程度上不依赖于初始权重(
![]() ,其中p = 10%, 20%, 30%, 40%, 50%),表明神经网络得到良好的充分训练。
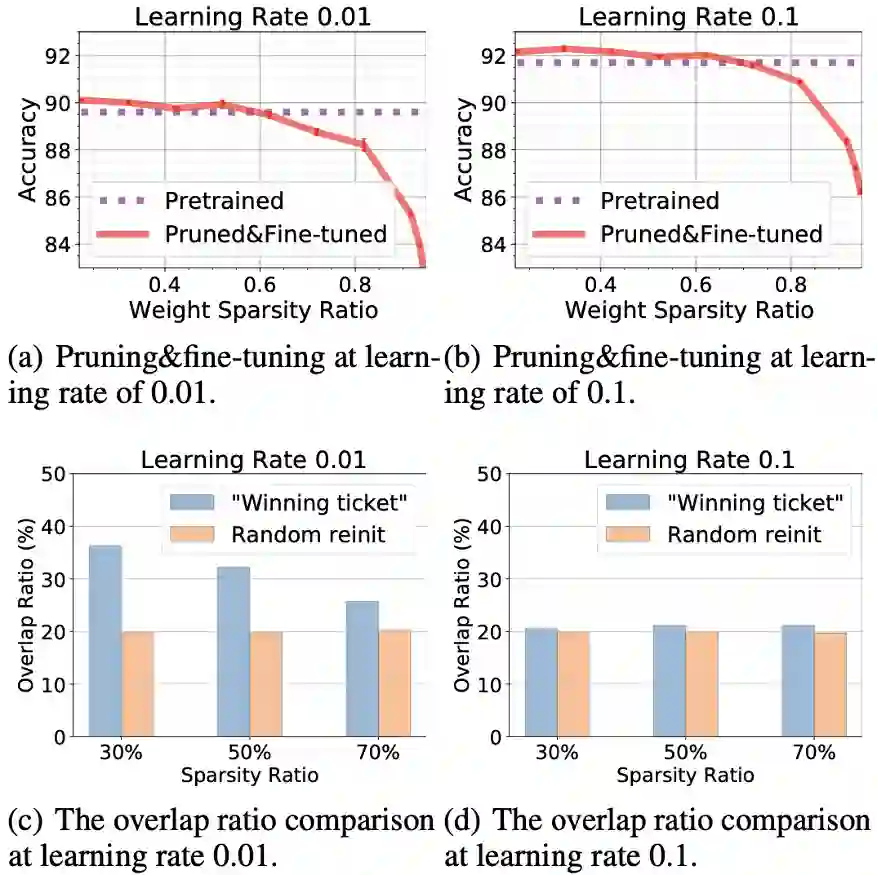
图5 (a),(b):在不同的稀疏率下,「剪枝与微调」
,其中p = 10%, 20%, 30%, 40%, 50%),表明神经网络得到良好的充分训练。
图5 (a),(b):在不同的稀疏率下,「剪枝与微调」
![]() 通过迭代剪枝算法产生的掩码的准确度。(c),(d):p =0.2时,在0.3、0.5、0.7稀疏度比下,「中奖网络」的权重
通过迭代剪枝算法产生的掩码的准确度。(c),(d):p =0.2时,在0.3、0.5、0.7稀疏度比下,「中奖网络」的权重
![]() 和「剪枝与微调」的权重
和「剪枝与微调」的权重
![]() ,以及重新随机初始化权重
,以及重新随机初始化权重
![]() 和「剪枝与微调」的权重
和「剪枝与微调」的权重
![]() 之间的权重相关性(重叠率)比较。
当学习率较低时,训练「中奖网络」和随机重新初始化网络的准确率不同,作者试图从这点出发,从而揭示出中奖属性的原因和条件。作者通过研究权重的相关性来实现这一目标。
作者尝试了「剪枝与微调」的方式,即对来自原始预训练网络的权重应用掩码,然后对其进行T轮微调。最终的权重表示成
之间的权重相关性(重叠率)比较。
当学习率较低时,训练「中奖网络」和随机重新初始化网络的准确率不同,作者试图从这点出发,从而揭示出中奖属性的原因和条件。作者通过研究权重的相关性来实现这一目标。
作者尝试了「剪枝与微调」的方式,即对来自原始预训练网络的权重应用掩码,然后对其进行T轮微调。最终的权重表示成![]() 。以CIFAR-10上的ResNet-20为例进行说明。从图5(a)和5(b)可以看到,
。以CIFAR-10上的ResNet-20为例进行说明。从图5(a)和5(b)可以看到,![]() 实现了相对较高的准确率,接近或高于相同学习率下的预训练DNN的准确率。
作者还研究了
实现了相对较高的准确率,接近或高于相同学习率下的预训练DNN的准确率。
作者还研究了![]() ,
,![]() 和
和![]() 之间的相关性,以便对中奖特性的原因有所了解。从图5(c)和5(d)可以观察到,在低学习率下,
之间的相关性,以便对中奖特性的原因有所了解。从图5(c)和5(d)可以观察到,在低学习率下,![]() 和
和![]() 之间存在较强相关性,这时存在中奖特性。在其他情况下,这种相关性很小或是没有。
结论是,中奖特性的一个关键条件是
之间存在较强相关性,这时存在中奖特性。在其他情况下,这种相关性很小或是没有。
结论是,中奖特性的一个关键条件是
![]() 和
和
![]() 之间的相关性。
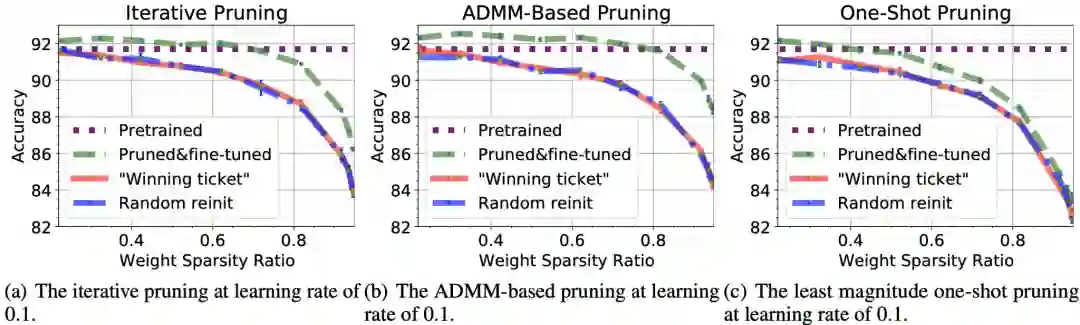
图6 「剪枝与微调」的精度表现与两种稀疏训练方案的比较(「中奖网络」和随机重新初始化)
图6展示了使用三种剪枝算法生成掩码:(a)迭代剪枝,(b)基于ADMM的剪枝,以及(c)一次性剪枝。
为了更好地克服「彩票假说」工作中稀疏训练的不足,作者提出「剪枝与微调」的方式。 作者以CIFAR-10数据集上的ResNet-20为例进行说明。这里使用理想的学习率0.1。
从图6可以清楚地观察到「剪枝与微调」与两个稀疏训练方案之间的精度差距。
事实上,「剪枝与微调」方案可以持续超越预训练的原始密集神经网络,其稀疏率可高达70%。同样,两个稀疏训练方案之间没有准确率差异。
图7 在三种剪枝算法(迭代剪枝、基于ADMM的剪枝和一次性剪枝)进行掩码生成下,「剪枝与微调」以及稀疏训练(「中奖网络」方案)的准确率表现。
图7结合了上述结果,展示了三种剪枝算法下的「剪枝与微调」以及稀疏训练(「中奖网络」方案)的准确率。可以观察到准确率的大小顺序:基于ADMM的剪枝最高,迭代剪枝在中间,一次性剪枝在最低。这个顺序对于「剪枝与微调」以及稀疏训练也是一样的。
在这里剪枝算法仅用来生成掩码。因此,相对准确率差异归因于生成不同的掩码的质量。可以得出结论,剪枝算法的选择在生成稀疏子网络中至关重要,因为生成的掩码的质量在这里起着关键作用。
在这项工作中,作者研究了彩票假说中中奖特性背后的基本条件和原理。引入了一个相关指标进行定量分析。在不同的数据集上对多个深度模型进行了广泛的实验,证明了中奖特性的存在与神经网络预训练不足有关,对于充分训练的神经网络来说不太可能发生。
同时,「彩票假说」工作中的稀疏训练设置很难恢复预训练的密集神经网络的准确率。为了克服这一局限性,作者提出了「剪枝与微调」的方式,该方式在相同的剪枝算法和总的训练时长下,在不同的数据集上对不同的神经网络均优于「彩票假说」工作设置的稀疏训练。
论文第一作者刘宁,博士毕业于美国东北大学计算机工程系,博士生导师为王言治教授。现任职美的资深研究员。
之间的相关性。
图6 「剪枝与微调」的精度表现与两种稀疏训练方案的比较(「中奖网络」和随机重新初始化)
图6展示了使用三种剪枝算法生成掩码:(a)迭代剪枝,(b)基于ADMM的剪枝,以及(c)一次性剪枝。
为了更好地克服「彩票假说」工作中稀疏训练的不足,作者提出「剪枝与微调」的方式。 作者以CIFAR-10数据集上的ResNet-20为例进行说明。这里使用理想的学习率0.1。
从图6可以清楚地观察到「剪枝与微调」与两个稀疏训练方案之间的精度差距。
事实上,「剪枝与微调」方案可以持续超越预训练的原始密集神经网络,其稀疏率可高达70%。同样,两个稀疏训练方案之间没有准确率差异。
图7 在三种剪枝算法(迭代剪枝、基于ADMM的剪枝和一次性剪枝)进行掩码生成下,「剪枝与微调」以及稀疏训练(「中奖网络」方案)的准确率表现。
图7结合了上述结果,展示了三种剪枝算法下的「剪枝与微调」以及稀疏训练(「中奖网络」方案)的准确率。可以观察到准确率的大小顺序:基于ADMM的剪枝最高,迭代剪枝在中间,一次性剪枝在最低。这个顺序对于「剪枝与微调」以及稀疏训练也是一样的。
在这里剪枝算法仅用来生成掩码。因此,相对准确率差异归因于生成不同的掩码的质量。可以得出结论,剪枝算法的选择在生成稀疏子网络中至关重要,因为生成的掩码的质量在这里起着关键作用。
在这项工作中,作者研究了彩票假说中中奖特性背后的基本条件和原理。引入了一个相关指标进行定量分析。在不同的数据集上对多个深度模型进行了广泛的实验,证明了中奖特性的存在与神经网络预训练不足有关,对于充分训练的神经网络来说不太可能发生。
同时,「彩票假说」工作中的稀疏训练设置很难恢复预训练的密集神经网络的准确率。为了克服这一局限性,作者提出了「剪枝与微调」的方式,该方式在相同的剪枝算法和总的训练时长下,在不同的数据集上对不同的神经网络均优于「彩票假说」工作设置的稀疏训练。
论文第一作者刘宁,博士毕业于美国东北大学计算机工程系,博士生导师为王言治教授。现任职美的资深研究员。
袁赓,美国东北大学计算机工程系博士在读生,导师为王言治教授。
参考资料:
[1] Frankle, J. and Carbin, M. The lottery ticket hypothesis: Finding sparse, trainable neural networks.
[2] Liu, Z., Sun, M., Zhou, T., Huang, G., and Darrell, T. Rethinking the value of network pruning.
[3] Frankle, J., Dziugaite, G. K., Roy, D. M., and Carbin, M. Stabilizing the lottery ticket hypothesis.
![]()
T轮(或更少)将达到与密集预训练网络
相似的准确率。
T轮和训练重新随机初始化稀疏子网络之间
应该有明显的准确率差距,前者应更高。
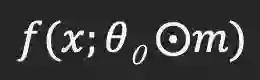 和训练
和训练
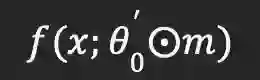 之间的精度差距。
之间的精度差距。
 和
和
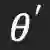 之间的最大幅值的部分权重的位置的重叠度。具体公式如下:
之间的最大幅值的部分权重的位置的重叠度。具体公式如下:
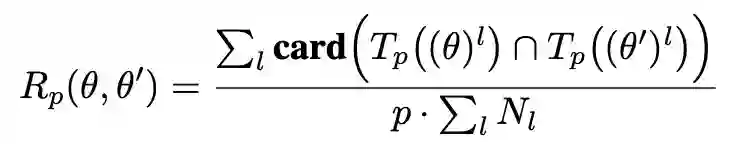
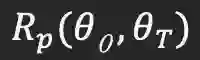 。
。
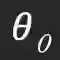 和来自神经网络预训练的权重的相关指标。与学习率为0.1的情况相比,学习率为0.01时相关性指标明显较高。
和来自神经网络预训练的权重的相关指标。与学习率为0.1的情况相比,学习率为0.01时相关性指标明显较高。
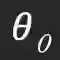 的较大幅值的权重没有被完全更新,说明预训练的神经网络没有被很好地训练更新。
的较大幅值的权重没有被完全更新,说明预训练的神经网络没有被很好地训练更新。
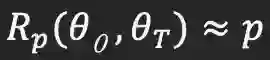 ,其中p = 10%, 20%, 30%, 40%, 50%),表明神经网络得到良好的充分训练。
,其中p = 10%, 20%, 30%, 40%, 50%),表明神经网络得到良好的充分训练。
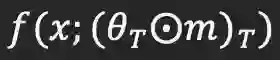 通过迭代剪枝算法产生的掩码的准确度。(c),(d):p =0.2时,在0.3、0.5、0.7稀疏度比下,「中奖网络」的权重
通过迭代剪枝算法产生的掩码的准确度。(c),(d):p =0.2时,在0.3、0.5、0.7稀疏度比下,「中奖网络」的权重
 和「剪枝与微调」的权重
和「剪枝与微调」的权重
 ,以及重新随机初始化权重
,以及重新随机初始化权重
 和「剪枝与微调」的权重
和「剪枝与微调」的权重
 之间的权重相关性(重叠率)比较。
之间的权重相关性(重叠率)比较。
 。以CIFAR-10上的ResNet-20为例进行说明。从图5(a)和5(b)可以看到,
。以CIFAR-10上的ResNet-20为例进行说明。从图5(a)和5(b)可以看到,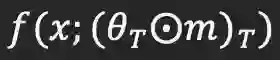 实现了相对较高的准确率,接近或高于相同学习率下的预训练DNN的准确率。
实现了相对较高的准确率,接近或高于相同学习率下的预训练DNN的准确率。
 ,
, 和
和 之间的相关性,以便对中奖特性的原因有所了解。从图5(c)和5(d)可以观察到,在低学习率下,
之间的相关性,以便对中奖特性的原因有所了解。从图5(c)和5(d)可以观察到,在低学习率下, 和
和 之间存在较强相关性,这时存在中奖特性。在其他情况下,这种相关性很小或是没有。
之间存在较强相关性,这时存在中奖特性。在其他情况下,这种相关性很小或是没有。
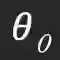 和
和
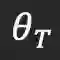 之间的相关性。
之间的相关性。


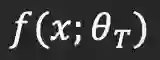 相似的准确率。
相似的准确率。 应该有明显的准确率差距,前者应更高。
应该有明显的准确率差距,前者应更高。

