NeurIPS 2021 Spotlight | 准确、快速、内存经济，新框架MEST实现边缘设备友好的稀疏训练

2022 年 1 月 1 日 机器之心

机器之心专栏

作者：袁赓

美国东北大学王言治教授、林雪教授研究组与威廉玛丽学院任彬教授研究组共同提出了一种稀疏训练新框架 MEST，有望在边缘设备上实现准确、快速以及内存经济的稀疏训练。

在剪枝技术被成功应用于神经网络的压缩和加速之后，稀疏训练在近年来受到了越来越多研究者的关注，即如何从零开始直接训练一个高质量的稀疏神经网络。稀疏训练旨在有效降低神经网络训练过程中的计算和存储开销，从而加速训练过程，为在资源有限的边缘设备上的神经网络训练提供了更多可能性。

多数现有稀疏训练方法着力于设计更好的稀疏训练算法来追求更高的网络稀疏度同时保持高准确率。然而，稀疏训练的关键，即稀疏训练能否带来实际的训练加速以及计算和存储资源的节省，却往往被忽视了。

为此，美国东北大学王言治教授、林雪教授研究组与威廉玛丽学院任彬教授研究组共同提出了 MEST 稀疏训练框架，有望在边缘设备上实现准确、快速以及内存经济的稀疏训练。该论文 [1] 已被 NeurIPS 2021 会议收录为 spotlight 论文。

论文链接：https://arxiv.org/abs/2110.14032

什么是稀疏训练？

我们知道通常的神经网络剪枝（pruning）方法是从一个训练好的密集模型（dense model）出发，通过应用剪枝算法去除模型中的冗余权重，来达到降低模型参数量和计算量的目的。而这个密集模型的预训练过程依然会耗费大量的计算资源。所以，近年来有越来越多的研究试图在预训练过程中直接使用稀疏模型（sparse model）进行训练，从而可以一步到位的获得最终的稀疏模型，我们可以管这个直接训练稀疏模型的过程叫做稀疏训练（sparse training）。稀疏训练可以有效的降低训练过程的计算量，并有望降低设备的存储开销以及加速训练过程。

稀疏训练大致可以分为两个类别，即静态稀疏训练（static sparse training）和动态稀疏训练（dynamic sparse training）。

静态稀疏训练通常会在训练的初始阶段通过使用相应的算法来确定稀疏网络的结构。之后，在整个的稀疏训练过程中始终保持相同的稀疏网络结构。静态稀疏训练的代表性工作有 SNIP [1] 与 GraSP [2] 等。此外，彩票假说（Lottery Ticket Hypothesis）[3] 中直接使用稀疏子网络进行训练的过程也可以被认为是静态稀疏训练。

动态稀疏训练一般会在训练的初始阶段随机或简单选择一个稀疏网络的结构作为起始，并在随后的稀疏训练过程通过中不断变化稀疏网络的结构，来达到搜寻更好稀疏结构的目的。动态稀疏训练的代表性工作有 DSR [5] 和 RigL [6] 等。相较于静态稀疏训练，动态稀疏训练往往更容易在高稀疏度下获得更好的稀疏模型准确率。

现有的先进稀疏训练方法中存在的问题

1. 非结构性稀疏方案 (Unstructured Sparsity Scheme)

绝大多数现有的先进的稀疏训练方法通常都会采用非结构性稀疏方案。这种稀疏方案允许任意位置的权重被移除。因此，稀疏模型的结构具有高灵活性，可以更好地在高稀疏度下维持稀疏模型的准确率。但是，与在剪枝技术中使用非结构性剪枝一样，由于非结构性稀疏模型中非零权重分布的不规则性，导致了硬件并行计算的不友好，比如不良的数据局部性（data locality）、负载不平衡（load imbalance）、线程分歧（thread divergence）和繁重的控制流指示（heavy control-flow instructions）等。这最终使得非结构性稀疏模型即便在高稀疏度下也很难实现可观的计算速度提升。

2. 内存不经济

为了能够找到更好的稀疏网络结构，在一些先进的稀疏训练方法中会使用到密集模型的信息，比如在静态稀疏训练中，一些方法会先进行少量次数迭代的密集模型训练来在初始化模型中找到想要的稀疏结构。同样，在动态稀疏训练中，一些方法会频繁地使用密集反向传播来计算出密集的权重梯度，从而指引稀疏结构的动态选择。虽然这些方法在大部分的稀疏训练过程中维持了稀疏模型的存储与计算，但是只要训练过程中涉及到密集模型的计算，就会极大地增加计算与存储资源的峰值使用量。这使得这些稀疏训练方法难以真正的在资源受限的边缘设备上进行端到端训练。

MEST 框架设计

为了解决以上提到的现有稀疏训练方法中存在的问题，我们认为在训练过程应当避免使用任何的密集模型的信息，保持整个训练过程的稀疏性。并且稀疏训练应当使用更加硬件友好的稀疏方案，从而达到真正加速训练的目的。此外，现有的稀疏训练方法多着眼于更好的算法设计，在保持稀疏模型准确率的情况下尽可能的提升模型稀疏率（sparsity ratio），从而进一步降低训练开销。然而，我们认为这并不是降低训练开销的唯一途径。提高对于训练数据的使用效率可以从另一个角度来进一步降低训练开销和加速训练过程，而这一角度被先前的稀疏训练研究忽视了。

1.MEST 稀疏训练方法

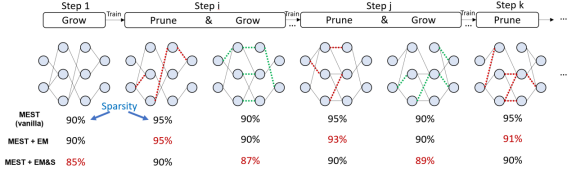
在我们的 MEST 稀疏训练框架中我们首先强调的是算法的内存经济性（Memory-economic）。我们采用传统的动态稀疏训练思想，通过在训练过程中不断地对稀疏网络的结构进行变异（mutation）来最终获得高准确率的稀疏网络。具体来说，为了使全部训练过程不涉及密集模型的存储和计算，我们在模型初始化阶段直接使用随机生成的索引（indices）以及 CSR 形式来直接存储随机初始化的稀疏模型。稀疏模型结构的突变过程可以看作是模型剪枝（prune）和模型生长（grow）的结合。首先，我们从稀疏模型（非零权重）中去除具有相对较低重要性的权重，再从不在稀疏模型中的权重中随机选择相同数量的权重加回到稀疏模型中，从而完成稀疏模型结构的突变，如图 1 中的 MEST（vanilla）方法所示。为了保持模型的稀疏性，我们直接将被去除权重的权重值设为零，并直接改变索引值，来实现模型结构的突变。

我们还提出一种弹性突变（Elastic Mutation）策略，简称 MEST+EM。我们的弹性突变策略意在整个训练过程中逐渐降低网络结构的突变率，如图 1 中 MEST+EM 方法所示。这样即保证了在网络训练过程中拥有足够大的搜索范围，同时在训练后期帮助稀疏网络结构更好的收敛，增加训练过程的稳定性。

此外，如果在应用场景中，内存占用可能是一个软约束，我们提出了一种稀疏训练的增强方法，称为软内存约束的弹性突变（Soft-bounded Elastic Mutation），简称 MEST+EM&S。

与 MEST+EM 方法不同的是，我们的 MEST+EM&S 允许将新增长的权重加入到现有的权重中，然后进行训练，随后从包括新增长的权重在内的权重中选择重要性较低的权重进行移除，如图 1 中 MEST+EM&S 方法所示。这可以避免在模型突变中强制移除比新增长的权重更正要的现有权重。所以我们的 MEST+EM&S 方法也可以被看做是在突变过程中增加了一个 "撤销" 机制。需要注意的是，虽然使用软内存约束会额外增加少量的内存和计算开销，但是整个稀疏训练过程仍处在高稀疏度下，且训练结束时仍然达到目标稀疏率。

图 1. MEST 框架中的稀疏训练方法

2. 探究不同的稀疏方案

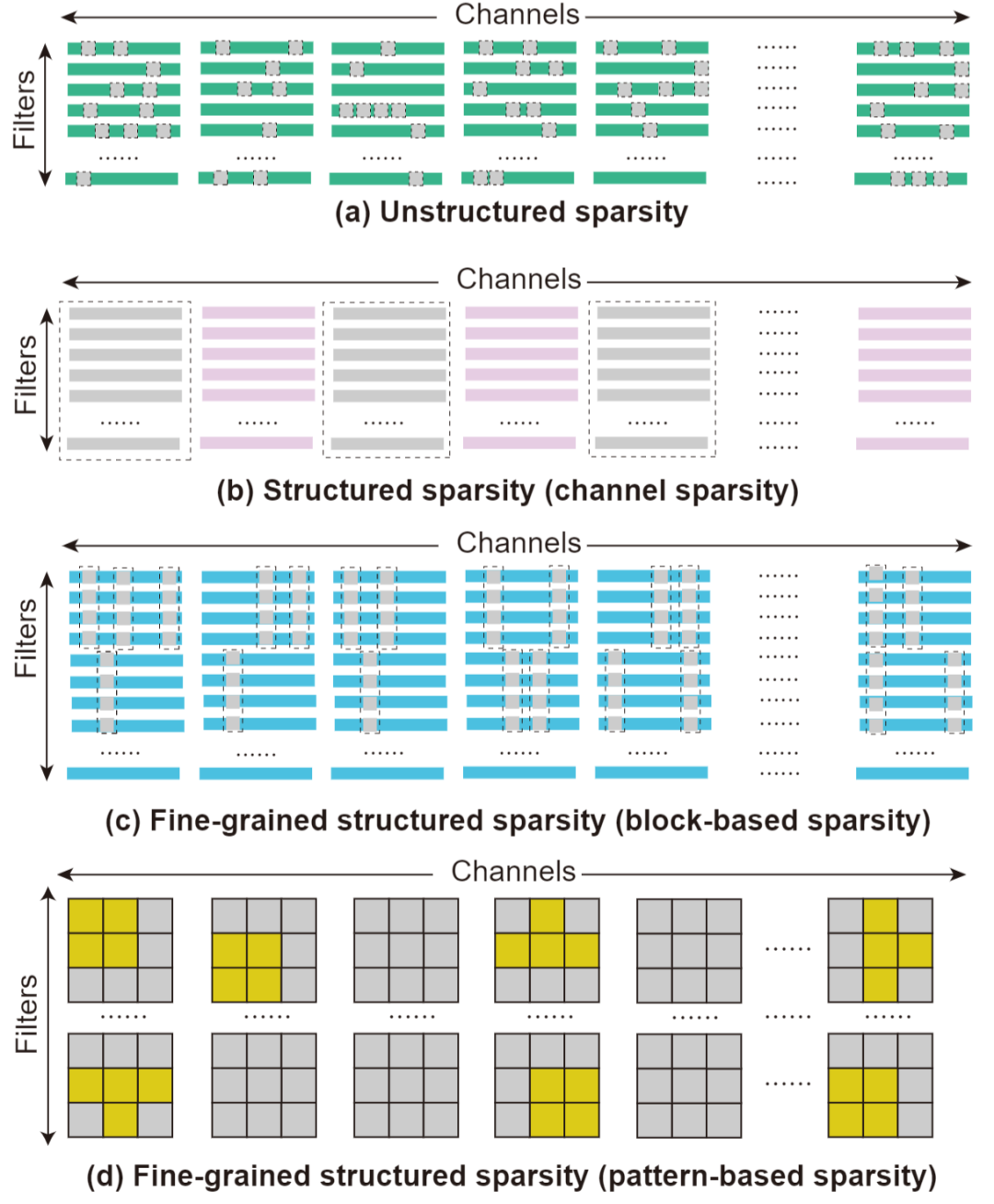
在 MEST 框架中，我们研究了不同稀疏方案在稀疏训练中的速度表现以及使用 MEST 方法的准确度。如图 2 所示，他们分别为（a）非结构性稀疏（unstructured sparsity）、（b）结构性稀疏（structured sparsity）、（c）基于区块的细粒度结构性稀疏（block-based sparsity）以及（d）基于模式的细粒度结构稀疏（pattern-based sparsity）。

图 2. 不同稀疏方案

如前面提到的，非结构性稀疏被广泛用于之前的稀疏训练研究。作为一种细粒度的稀疏形式，其具有高灵活性，可以更好地维持网络的准确率，但是很难达到可观的加速。我们在 MEST 中也对非结构性稀疏进行测试，以便从算法角度与之前的工作进行公平比较。同时，在对比不同稀疏方案的准确率表现时将其视为准确率上限。

我们还测试了结构性稀疏方案，即移除整个卷积滤波器（filter）或卷积通道（channel）。这种粗粒度的稀疏方案非常硬件友好，可以实现较高的加速性能，但是往往模型准确率会极大地降低。

在基于区块的细粒度结构性稀疏方案中，我们将权重矩阵分为若干个等大小的块，然后在每一个块中选择整行或整列进行权重的稀疏化，在不同的块中稀疏行列位置和数量可以不同，这样提高了稀疏的灵活性，从而保持更好的模型准确率。由于受到硬件并行度的限制，即便将权重矩阵进行分割，每一个块依然可以很好地满足高计算并行度，所以这种相对细粒度的结构性稀疏可以达到较高的加速效果。

基于模式的细粒度结构稀疏结合了卷积核模式稀疏和连通性稀疏。其中，卷积核模式稀疏从每一个滤波器的卷积核中将给定数量的权重设为零，使得剩余非零权重形成特殊的模式。图 2（d）所示为在 3x3 卷积核中使用 4 非零权重模式。此外，连通性稀疏择将整个卷积核移除，从而进一步提升基于模式的细粒度结构稀疏方案的整体稀疏度。

这两种稀疏方案通过细粒度的稀疏性在一定程度上保证了稀疏结构的灵活性，从而有效的提高模型准确率。同时，他们又满足一定的结构约束，使得这种稀疏结构可以在编译器优化的帮助下实现较高性能的加速。我们在稀疏训练过程中，分别将不同的稀疏方案应用在我们提出的 MEST+EM 和 MEST+EM&S 方法中来探究不同稀疏方案在准确率和加速性能等方面的表现。

3. 数据效率在稀疏训练中的应用

除了不断增加模型的稀疏度，在稀疏训练中使用更高效的训练数据同样可能有效的加速训练过程。经过证明，对于网络训练来说，每个训练样本的学习难度是不同的，同时其能提供给网络训练的信息量也是不同的 [7]。一些训练样本在训练的早期阶段就可以被网络学会（正确识别），其中一些样本在被网络学会之后就不会再被错误识别，换言之，他们永远不会被网络遗忘。这里我们定义当一个训练样本在被网络正确识别后又被错误分类为一次 “遗忘事件”。

如图 3 所示，左手边展示了两个不同的青蛙训练样本。上面的训练样本在整个训练过程中被遗忘了 0 次，所以我们也称它为不被遗忘的样本（unforgettable example），而下面的样本则被遗忘了 35 次。同时，通过观察对比图 3 右侧的具有高遗忘次数和低遗忘次数的训练样本，我们可以看出一般具有较低遗忘次数的样本通常比较简单，既样本具有鲜明的特征且背景较为简单。因此，之前的工作使用遗忘次数作为衡量训练样本难易程度的标准，并且发现容易的样本为网络训练提供的信息量较少，如果将不被遗忘的样本从训练数据集中移除，训练出的网络依然可以达到与完整数据集相当的准确率，但是训练速度因训练数据集的减小而加快。

图 3. 不同训练样本具有不同遗忘次数

然而，对于数据效率在稀疏训练场景下的探索仍然是缺失的。由于稀疏模型的容量较小，且模型结构是动态变化的，是否可以利用数据效率来进一步加速稀疏训练仍是未知数。因此，我们希望研究稀疏率、稀疏方案和变异机制对可移除训练样本数量的影响，然后讨论利用数据效率加速稀疏训练的可能性。

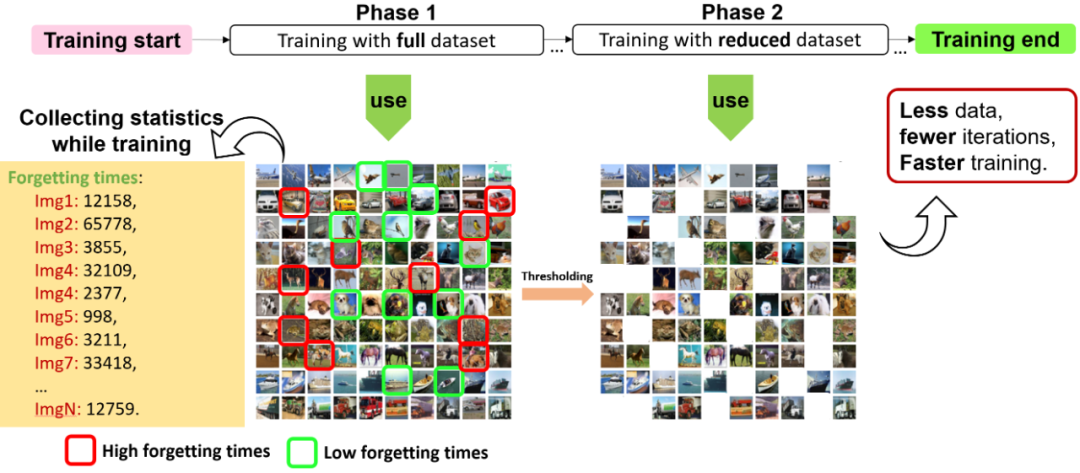
之前的工作使用了整个训练过程来进行训练样本难易度的统计工作，而我们希望通过引入数据效率来进行训练加速，所以我们提出了一种两阶段数据高效训练方法。我们使用与常规训练相同的训练周期数，并将训练过程分为数据统计阶段与使用部分数据集的高效训练阶段，如图 4 所示。我们在 MEST 框架中将这种数据高效方法与我们提出的稀疏训练方法相结合，既在两个阶段中均使用 MEST+EM 或 MEST+EM&S 稀疏训练。

图 4. 两阶段数据高效训练方法

实验结果

1. 稀疏算法对于数据效率的探究

首先，我们对在动态稀疏训练中引入数据高效训练进行了多方面的探究。

模型稀疏度、稀疏算法对不被遗忘的样本数量的影响：

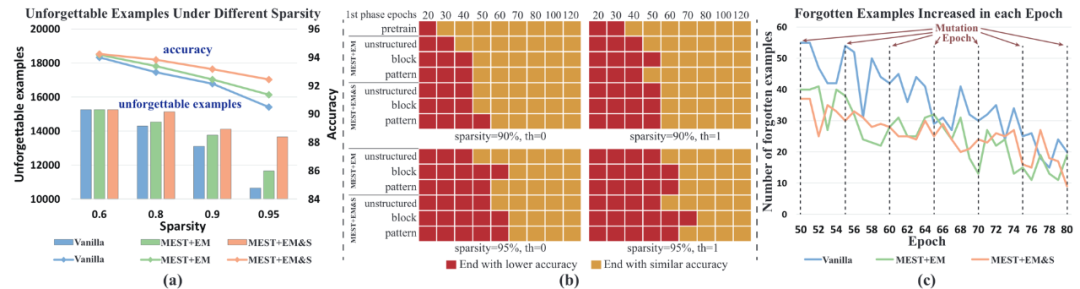
我们首先测试了不同的稀疏训练方法对于不被遗忘的样本数量的影响，结果如图 5（a）所示，随着模型稀疏度的增加，不被遗忘的样本数量在减少，并且与模型的准确率呈现正相关。原因是在高稀疏度下，模型的泛化性能下降，使得一些简单的样本更难记住。此外，我们还观察到，更好的稀疏度训练方法（如 MEST+EM&S）会增加不被遗忘的样本数量，这表明在不影响模型准确率的情况下，有机会去除更多的训练样本，从而获得更高的训练加速。

图 5. 数据高效训练的探究。(a) 在不同的稀疏训练算法和稀疏率下，整个稀疏训练过程后不被遗忘的样本数量；(b) 在稀疏率为 90% 和 95% 下，移除被遗忘次数分别为 0 和 1 的样本，所使用的样本数据统计阶段（第一阶段）的周期数及其相应的模型最终准确率状态；(c) 每个训练周期中增加的遗忘例子的数量（在训练周期 50 到 80 之间，稀疏结构突变频率为 5 个周期）。结果为 ResNet-32 网络在 CIFAR-10 数据集上的表现。

两阶段数据高效训练中数据统计所需周期数：

为了在一个常规的训练长度中实现数据统计以及数据高效训练，我们需要在第一个阶段统计样本的难易程度，以便在第二阶段将简单样本从数据集中移除。由于数据高效训练仅在第二阶段中拥有加速效果，所以我们希望使用尽可能少的训练周期完成第一阶段的数据统计工作。然而，在训练初期，由于网络没有被良好的训练，可能确保所统计出的难易程度的准确性，从而会影响最终数据高效训练模型的准确率。因此，我们观察了不同第一阶段周期数与最终模型准确率的关系。

如图 5（b）所示，红色代表在相应的第一阶段周期数下，最终模型的准确率低于使用完整数据集的准确率，而黄色代表使用相应的第一阶段周期数可以达到与使用完整数据集相同的准确率。同时，我们研究了不同稀疏训练方法、稀疏结构方案、模型稀疏率、以及移除的样本数量，所需要的第一阶段的训练周期。通过对比结果，我们可以在保持最终准确率的情况下，选择最少的第一阶段周期数量来获得最高的训练加速。

模型结构变异是否会导致遗忘？

不断进行的模型结构变异作为动态稀疏训练的一大特征，是否会导致模型对以学会样本的严重遗忘是我们在稀疏训练中引入数据高效训练关注的问题。为此，我们观察了每次模型结构突变前后的相邻周期中被遗忘样本数量的变化。

图 5（c）显示了不同稀疏训练方法从第 50 到第 80 个训练周期，每个训练周期中被遗忘的样本数量的增多值，也就是两个连续的训练周期中被遗忘样本的差异。我们可能会直观的认为，模型结构的频繁变异会导致明显的遗忘现象发生。但是，令我们惊讶的是，被遗忘的样本数量在模型结构变异的训练周期与非变异的训练周期并无明显差异，这表明模型结构的变异并不会加剧遗忘现象。这是因为每次变异的权重均为相对最不重要的权重，因此对模型的性能影响很小。

2.MEST 框架的准确率与加速性能表现

训练方法有效性检验：

首先，我们对 MEST 框架中所提出的稀疏训练方法的进行了准确率方面的测试，并与具有代表性的稀疏训练方法进行了比较。为了进行更公平的比较，我们 MEST 在这里也使用了跟其他方法一样的非结构性稀疏方案。

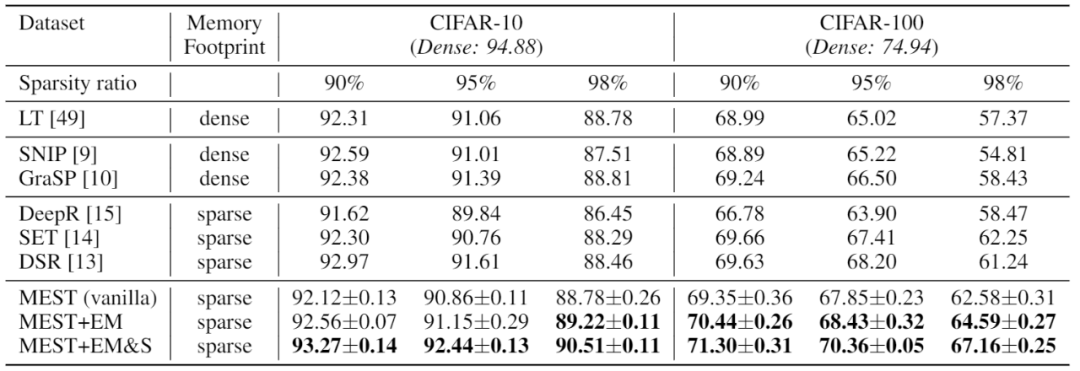
我们在 CIFAR-10 和 CIFAR-100 数据集上对 MEST 框架中使用的 MEST+EM 和 MEST+EM&S 方法进行了稀疏训练模型准确率的测试。我们对比了具有代表性的静态稀疏训练方法以及不需要涉及密集信息的动态稀疏训练方法。可以看出，我们的 MEST+EM 方法在 CIFAR-10 上达到与参考方法相似或更高的准确率，在 CIFAR-100 上我们的 MEST+EM 方法具有更高的准确率优势。此外，我们的 MEST+EM&S 方法可以显著的进一步提高稀疏训练准确率。

表 1. 在 CIFAR-10 和 CIFAR-100 上使用 ResNet-32 与 SOTA 工作的准确率比较。

虽然现今在端设备上使用庞大的 ImageNet 数据集进行训练并不实际，但是为了进一步验证我们的稀疏训练方法的有效性，我们同样在 ImageNet 数据集上进行了准确率的测试。

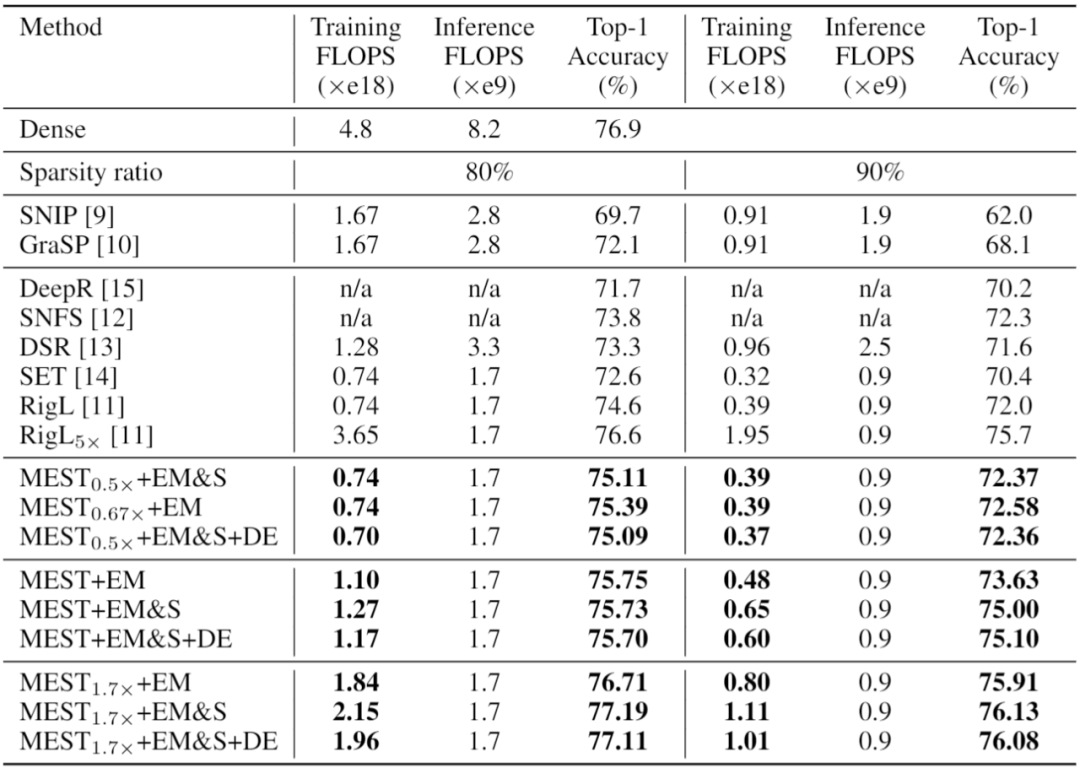
如表 2 所示，与先进的 RigL 方法相比，我们的 MEST+EM 和 MEST+EM&S 方法可以在相同的训练计算量（FLOPs）下，得到更高的稀疏训练准确率，且我们的方法在训练过程中不涉及任何密集模型信息，因此更加的硬件友好。此外，我们还测试了引入数据高效训练的效果（MEST+EM&S+DE）。可以看到，我们的数据高效训练方法可以在保持准确率的同时，进一步减少训练开销，从而实现训练加速。

表 2. 在 ImageNet 上使用 ResNet-50 与 SOTA 工作的准确率比较。

不同稀疏方案的准确率与加速性能表现：

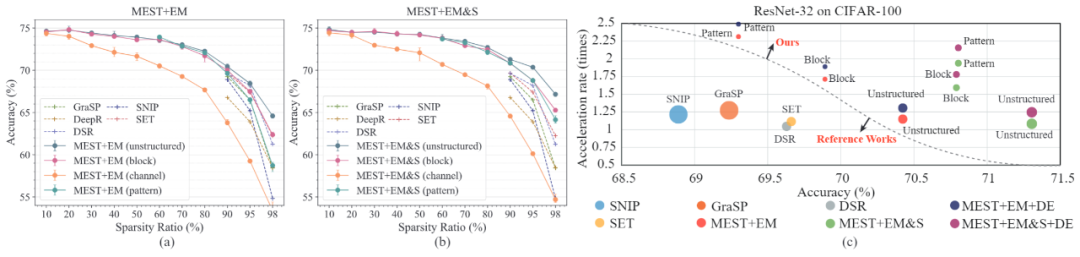
我们在这篇工作中探究了不同稀疏方案在稀疏训练中的准确率与加速性能的表现。如图 6 （a）和（b）所示，粗粒度的结构性稀疏方案会产生较大的准确率下降，而两种细粒度的结构性稀疏方案（基于区块的细粒度结构性稀疏方案与基于模式的细粒度结构稀疏方案）则可以在高达 90% 的稀疏度下达到与非结构性稀疏方案相似的准确率。图 6（c）展示了在 90% 稀疏度下，不同方法和稀疏方案在准确率、训练加速率以及相对存储资源的对比。我们可以看到，即便在如此高的稀疏度下，所有的非结构性稀疏方案都无法达到可观的加速性能，而细粒度的稀疏方案可以在保持较高准确率的情况下，大大提升加速性能。同时，我们的数据高效训练可以进一步有效地提升训练的加速。

图 6. 不同稀疏方案在不同稀疏度下的模型精度对比。

结语

由于现有的稀疏训练工作普遍忽视了稀疏方案对实际加速性能的影响，以及对稀疏训练方法是否内存经济且硬件友好的顾虑，我们提出了 MEST 稀疏训练框架，通过简单且有效的稀疏训练方式和适当的稀疏方案，实现准确、快速以及对边缘设备友好的稀疏训练。我们研究了不同稀疏方案对于稀疏训练准确率以及加速性能的影响。同时，我们提出引入数据高效训练方法来作为模型稀疏度的补充。我们探究了数据高效训练在稀疏训练场景下的特性，并提出一种两阶段数据高效训练方法，并在不影响准确率的情况下进一步加速了稀疏训练过程。我们也希望这种新的稀疏训练加速思路可以被更广泛的研究。

参考文献：

[1] Yuan, Geng, et al. "MEST: Accurate and Fast Memory-Economic Sparse Training Framework on the Edge." NeurIPS 2021.

[2] Lee, Namhoon, et al. "Snip: Single-shot network pruning based on connection sensitivity." ICLR 2019.

[3] Wang, Chaoqi, et al. "Picking winning tickets before training by preserving gradient flow." ICLR 2020.

[4] Frankle, Jonathan, et al. "The lottery ticket hypothesis: Finding sparse, trainable neural networks." ICLR 2019.

[5] Mostafa, Hesham, et al. "Parameter efficient training of deep convolutional neural networks by dynamic sparse reparameterization." ICML 2019.

[6] Evci, Utku, et al. "Rigging the lottery: Making all tickets winners." ICML 2020.

[7] Toneva, Mariya, et al. "An empirical study of example forgetting during deep neural network learning." ICLR 2019.