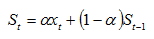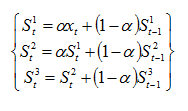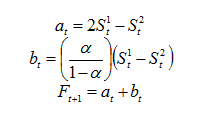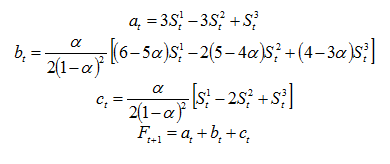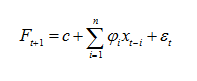你真的懂时间序列预测吗？

| 导语 起初做时间序列预测时，把教科书、网上教程、实战案例、各种资料扒拉了不少。ARIMA、SARIMA、RNN这些家喻户晓的模型也使了个遍，可结果却依然解决不了实际问题。于是静下心来仔细琢磨，发现之前的思路原来漏洞百出。潜心研究，渐渐的，有了自己的招数。

一、简介

时间序列，是一组按照时间发生先后排序的数据点序列，比如5分钟的在线序列、秒级的流量统计序列等。

时间序列预测，就是预测未来一段时间的数据点。

做时间序列预测的目的，运维工作中，常见的有两个：为未来某个时间点做资源预估，如大版本发布、节假日活动等；监控告警，判断当前的数据点是否有异常，如在线监控、流量监控等。

关键词：时间序列预测、异常检测、指数平滑、Holt-Winters、线性回归

二、 问题分析

背景介绍完了，下面是一个看上去很美的教程，寻找跟我一样的受害者。

2.1 案例

        采用算法：Arima系列

        输入序列：历史若干个数据点

        输出序列：未来若干期预测点

        步骤：各种序列校验、参数选择，教程随手可见，略过

        效果图：源自网络

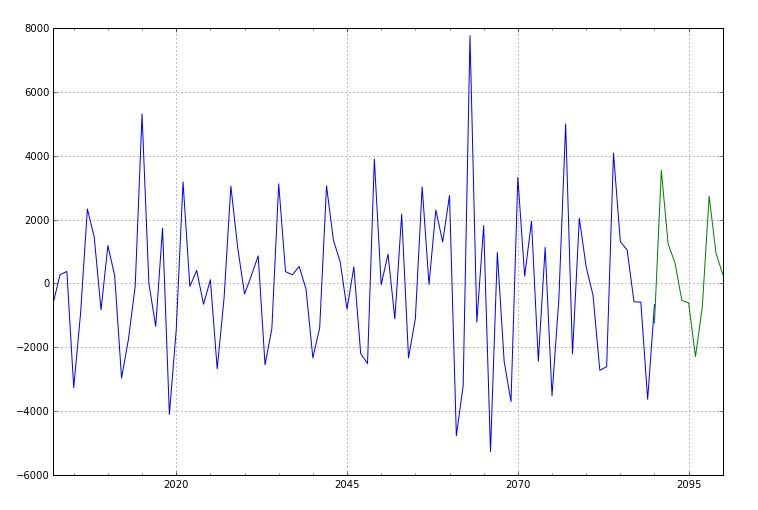
图1 Arima预测结果

        图1中蓝色线为历史序列，绿色线为预测序列。预测结果看起来还行，起码长得和输入序列挺像。

        一切看似很顺利，但这真的能解决我们的实际问题吗？分析问题总不能脱离场景需求：

2.2 需求

        当时我们团队需要做的是异常检测，而时序预测是其中的一步。这就决定了，我们只需要预测未来一期的数据点，并与实际观测点做对比，作为异常检测的依据。

        结合2.1的案例发现其不符合我们的需求：

• 例子中预测了多期的数据点，我们只需要动态预测未来一个数据点，长期预测与短期预测选用的算法截然不同。

• 例子中的曲线周期短且固定，运维中的曲线周期则至少为一天，包括上百个数据点，所以arima系列完全无法胜任。

        类似的故事还发生在时间序列分解、离散傅立叶变化等，大部分都存在算法很经典但场景不适用的问题，相信一定有很多同学和我们做过同样的尝试。

        踩坑过程略过……后来的后来，总结出了正确的姿势。

三、 解决方案

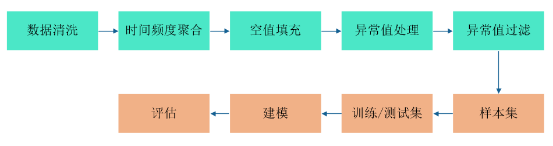
图2 时间序列预测

        整体方案见图2，其中蓝色部分不再赘述了，方法大同小异。分歧往往发生在红色部分。

3.1 样本集

        处理好的时间序列就是一个按时间排序的一维数组，但这还不是我们预测模型的输入样本。

        用于训练预测模型的样本，应该具备这三个要素：

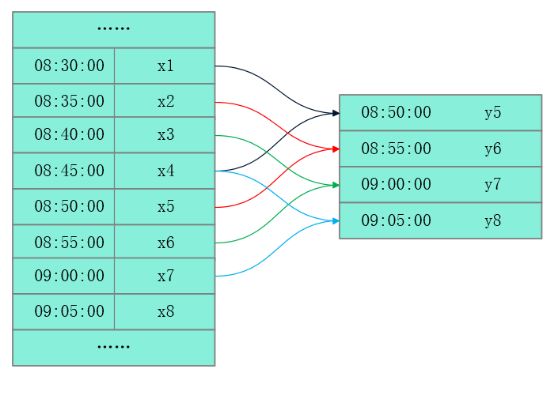
图3 样本集示意图

• 一致的输入：图中x1,x2,x3,x4为一组输入，每组输入的长度必须相同

• 明确的输出：图中y5为一次预测结果，x5为预测目标

• 样本集：多组成对的输入+输出的集合

• 
  

        对比之下，不难发现2.1的案例存在另一个问题，arima模型实际上只有一组输入输出，然后进行递推预测多期数值。而要满足我们的实时监控需求，就需要对每一个数据点训练独立的arima模型，然后把预测的误差作为我们后续异常检测模型的样本，这种做法的算力消耗是极高的。同理，时间序列分解也会面临类似的问题。

        样本集处理好之后，接下来划分训练集与测试集，可以参照样本集划分

3.2 时序预测算法

        训练集准备妥当，就可以开始训练预测模型了。个人将常见的短时预测算法分为两大类：趋势延伸，回归。

3.2.1趋势延伸

        趋势延伸指根据序列的时间变化趋势，对未来短期内的数值进行预测。常用的方法包括移动加权平均、指数平滑、Holt-winters等。这些算法的特点是即拿即用，不需要训练，只需要设置少量超参（若自动调参则需要训练）。以指数平滑为例。

        指数平滑时序预测

        指数平滑是一种递推式的预测算法，其通式为

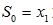
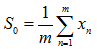
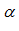
        其中，xt为t时刻的时间序列数值，初始值或，为权值。

        可以看出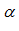越小，衰减越慢，历史值对预测值的影响越大。

        于是，曲线越平滑、趋势变化越快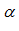，需要相对较大；反之，若曲线局部为锯齿形、且整体变化趋势缓慢，

可以相对较小。更具体的调整还是需要依据各项评估指标。

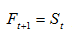
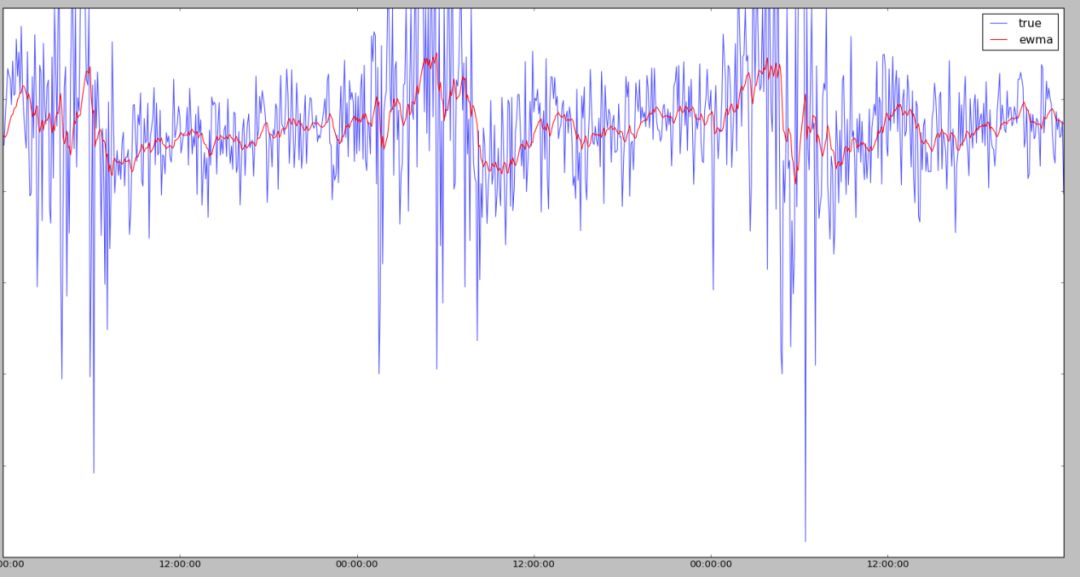
        对于一次指数平滑，即将当前点的指数平滑结果，作为下一个点的预测值。所以，一次指数平滑预测存在滞后性，适合锯齿状变化缓慢的曲线，并且平滑的作用大于预测，如下图：

图4一次指数平滑结果

        二次指数平滑和三次指数平滑在平滑的基础上，加入了趋势预测部分。

        首先，对原序列进行多次平滑：

        在此基础上，二次平滑预测为：

        三次平滑预测为：

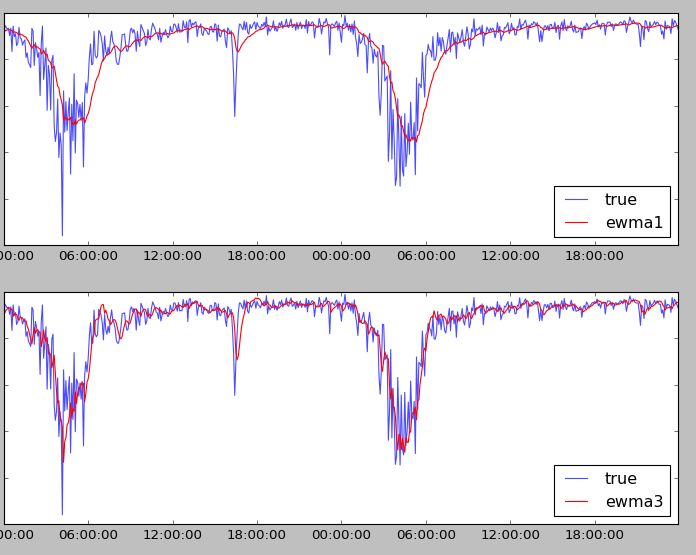
        附上三次指数平滑与一次指数平滑的对比图：

图5一次指数平滑与三次指数平滑

        图5中上图为一次指数平滑结果，下图为三次指数平滑结果，可以看出，高次指数平滑缓解了预测的滞后性，具有更强的趋势预测能力。但需要注意，趋势预测难免具有一定的”惯性”，需要特殊处理。

        除此之外，还有很多趋势延伸类的预测方法，如Holt-winters等。

3.2.2 回归

        回归指通过建模，寻找输入与输出的函数关系，从而进行预测。与前文趋势延伸不同的是，回归建模需要从大量历史数据中学习到模型参数，例如线性回归的权重与截距，AR模型的自回归系数等。

        回归建模一般可分为两个部分：特征与模型

        模型指我们有一个既定结构的回归模型 f(x)，其中x是输入，也就是特征。

        时序预测问题对回归模型的拟合能力要求不高，基本上线性回归就足够了。更复杂的模型会拟合能力溢出，很容易导致过拟合。

        对于特征的选择，我们可以简单粗暴的将预测点之前的n个点作为特征，也就是自回归模型。自回归可以看作是线性回归的一种形式。

        也可以计算出时间序列的多阶多步差分序列，并将其作为回归输入特征。这样做的目的是通过先验知识，告诉模型应该多关注数值的变化趋势而不是数值本身。此外，还可以加入各种先验特征，以满足不同的需求。

四、 成果

        我们的最终目的是监控告警，基于时序预测的告警模型，目前已接入数十款业务，广泛应用于在线、登录、登出、耗时等多个使用场景，可以通过多米诺、GEM一键接入，也可以直接在蓝鲸数据平台使用我们公开的算法节点建立定制化告警。

        不同于传统监控，告警模型完全是数据驱动的，彻底告别人为设定告警策略。通过对历史数据的学习，得到自适应的模型，在接入效率、准确率方面，全面超越传统告警，下图为监控结果，图片来自多米诺：

图6 告警结果

        图6中两种不同波动的曲线，接入方式没有区别，模型可以自适应的调整参数配置，做到平滑曲线（上图）不漏告，波动曲线（下图）不误告。不同业务不同场景的时序曲线均可以批量接入，彻底告别人为设置告警策略。

图7告警结果

        图7中，上图红线为告警点，下图为告警时间段缩放。可以看出，告警点的曲线上升趋势发生了变化，而结合时序预测的异常检测算法可以准确的检测出这种变化。

五、 思考

5.1 周期性

        运维工作中遇到的曲线通常会表现出周期性，比如在线曲线。而短时预测模型是很难学习到曲线周期性的。

        主观原因是曲线周期通常大于一天，而预测模型输入只是历史若干个点。这个差异导致模型很难学习到周期性。并且，这种现象不会因为模型复杂度的上升而得到明显改善。

        客观原因是曲线周期性并不稳定。以天为周期的话，工作日与周末的差异难以遵循；以周为周期的话，节假日难以处理；还有游戏周期性行为、季节性活动等等。此外，受到业务所处的不同阶段的限制，我们很难收集到稳定、大量的历史数据。

        针对这种情况，我们将周期的问题留在异常检测阶段处理，而不在短时预测部分加入过多判断逻辑。

5.2 分布预测

        其实回归模型可以结合深度学习等前沿技术，从而将模型做得很复杂，对于图4、图5中有大量噪音的曲线，最近的研究成果是采用深度学习的方式进行分布预测，将时序预测与异常检测整合进一个端到端的神经网络模型中，这也是我们接下来的一个探索方向，欢迎感兴趣的同学一起交流。

购物圣经小红书翻红之路

更新微信7.0版后

腾讯用AI种黄瓜，程序员忍了四个月，终于拍了它

“人肉流量”制造业：300万真人堆砌起的流量迷局