决策树之玩转借贷俱乐部

引言

在线性回归之玩转金郡和对率分类之玩转美亚中，斯蒂文帮助老板建的房价预测模型和婴儿产品推荐模型让老板很满意。最近老板接到借贷俱乐部 (lending club) 的一个项目，就是根据借款者的信息来判断这笔贷款是否有风险。

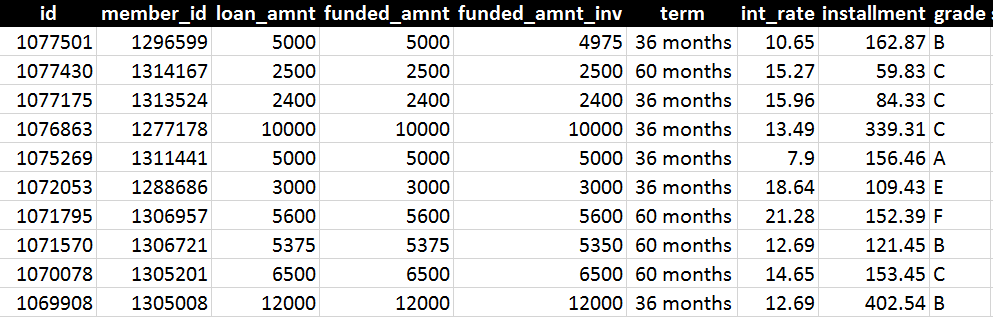
老板给了斯蒂文一份 csv 数据里面记录着 122,000 多条数据 (每条数据有 68 个特征)，下图选了几条不完整的信息展示：

上图记录着一些重要特征如 loan_amount, term, int_rate 和 grade，分别指是贷款本金、年限、利率和评级。

经过一周的努力，斯蒂文用下面的方法一步步探索了借贷俱乐部的数据

• 首先预处理数据

• 再用 sklearn 自带树模型

• 然后自己编写决策树模型

• 最后修剪树而防止过拟合

进入王的机器公众号，在对话框回复 ML14 可下载代码 (ipython notebook 格式) 和数据 (csv格式)

目录

第一章 - 数据预处理

    1.1 引用包

    1.2 研究数据

    1.3 处理数据

第二章 - 决策树 (sklearn)

第三章 - 决策树 (MM)

    3.1 子函数

    3.2 构建决策树

    3.3 可视化决策树

第三章 - 决策树 (pruning)

    3.1 子函数

    3.2 构建决策树

    3.3 探索决策树

下面斯蒂文用 ipython notebook 带你们玩转借贷俱乐部。

第一章：数据预处理

1.1

引用包

本贴需要的包有：

• numpy: 提供快速数字数组结构和辅助函数

• pandas: 提供一个数据表结构并能高效的处理数据

• sklearn: 用于机器学习

• matplotlib: 用来画图

此外 train_test_split 是用来划分训练和测试集，而 tree 是 sklearn 自带的决策树模型，可以直接拿来用。

1.2

研究数据

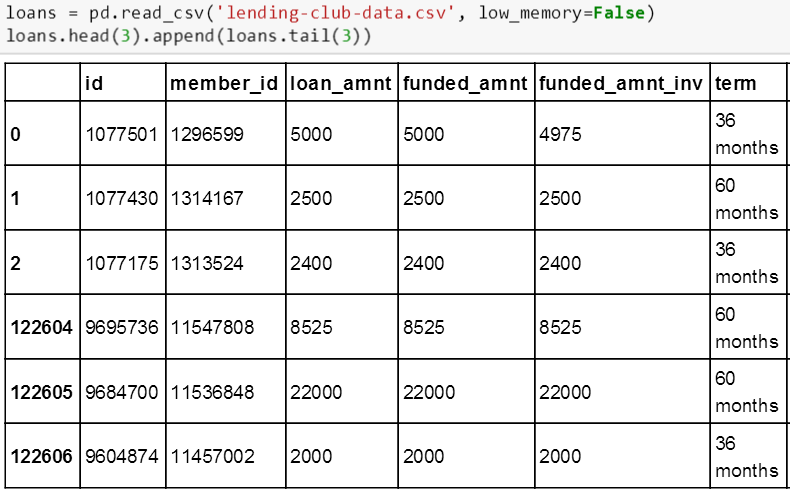
用 pandas 里面的 read_csv 函数来读取数据并存储到数据表 products 里面，再用 head(3) 和 tail(3) 函数看前三行和后三行的数据。

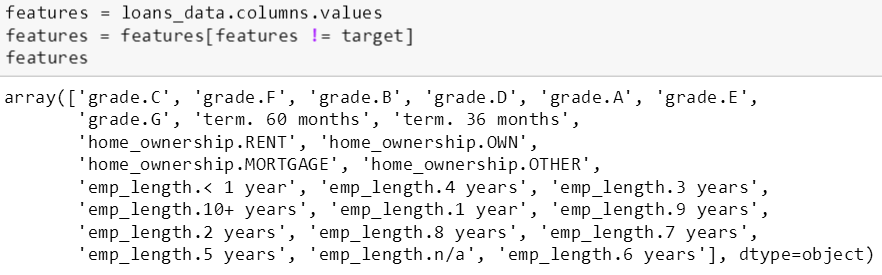
而用 columns.values 函数可以看到 loans 里面有那些具体特征。

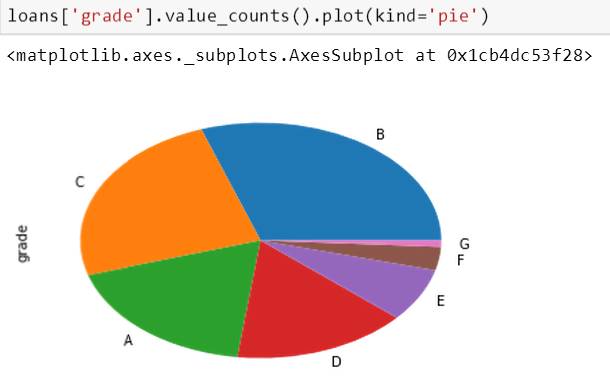
接着斯蒂文想看看数据的评级 (grade) 和房屋所有权 (home ownership) 里面的分布。

以上代码里 value_counts() 是对每个评级里的数据做计数，而 plot(kind='pie') 是将这些计数用饼状图画出来。从上图可知评级为 B 和 C 的两类贷款占了全部贷款的一半。

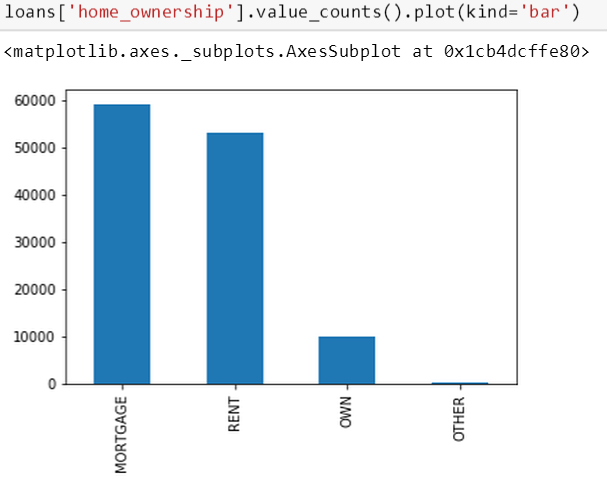
以上代码里 value_counts() 是对每个房屋所有权里的数据做计数，而 plot(kind='bar') 是将这些计数用条形图画出来。从上图可知只有一小步部分房屋是被完全拥有的。

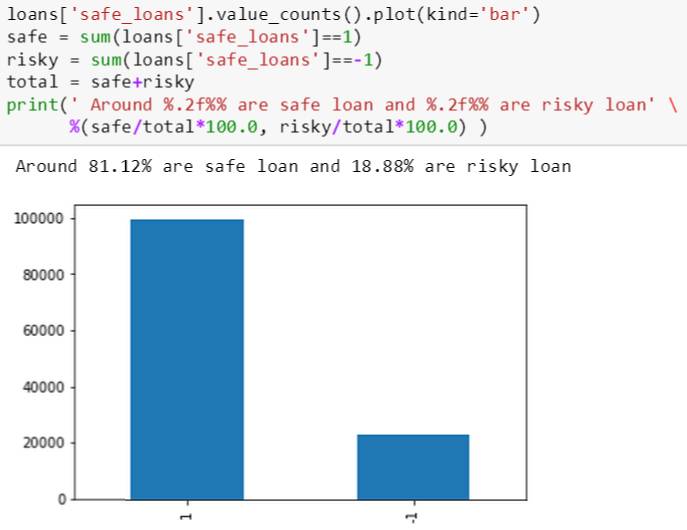
csv 里面有一栏 (标签) 叫 bad_loans，其中 0 代表良性贷款 1 代表恶性贷款。本章用 -1 和 1 代表良性贷款和恶性贷款。以下的代码将 bad_loans 的 0 和 1 转换成 safe_loans 的 1 和 -1。

之后画出良性贷款和恶性贷款的条形图 (如下图) 并计算其百分比为 81% 比 19%，发现贷款的好坏比例严重不平衡。这回使得分类问题变得不那么容易。

1.3

处理数据

用表格和图对数据有个大概了解之后，斯蒂文需要处理数据以便于 sklearn 的 tree 自带模型直接使用。接下来有三个问题需要处理：

1. 平衡样本 (sample balancing)

2. 特征子集 (feature subset)

3. 独热编码 (one-hot encoding)

平衡样本

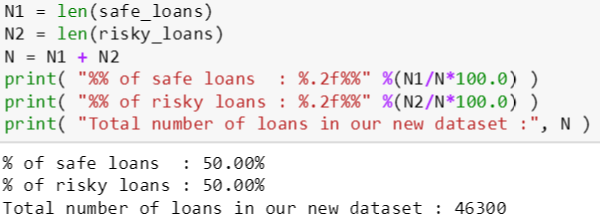
首先计算出好坏贷款的个数，并计算出它们的比例 ratio，由上节结果知道好贷款比坏贷款多 (大概 4 倍左右)，因此在好贷款中随机选取 1/4 和原先的坏贷款组成 (用 append() 函数) 新的贷款数据。这是一种欠采样的方法，即去除一些正例使得正反例数目相近，然后在进行学习。但是欠采样法可能会丢失一些重要信息。业界通常用集成学习机制 (ensemble method)，将正例划分给几个集合供不同模型使用，这样对每个模型来看都是欠采样，但在全局来看确不会丢失重要信息。在本贴重要是为了平衡化样例类别，就不深究那些复杂采样的方法了。

现在好坏贷款的比例是一比一，我们也发现总样例数从 122607 减少到 46300。

特征子集

根据经验或一些特征选择技巧 (这里不讨论)，斯蒂文只用评级，年限，房屋所有权和工作年数这四个特征对贷款是否良性恶性做决策。

精简之后的 loans_data 展示如下，斯蒂文发现一个问题，就是所有特征对应的值都是分类字符型变量而不是数值型变量，而且 sklearn 里面的树模型需要数值型变量。下节的独热编码可以解决此问题。

独热编码

独热编码是一种把分类字符型变量转换成 0/1 数值型变量的技巧，比如对 home_owernship 特征来说，它对应特征值只包含 RENT, OWN 和 MORTGAGE 这三个。

第一条数据的 home_owernship 特征是 RENT，可写成

    {‘home_owernship’: 'RENT'}

根据独热编码， 斯蒂文将上面特征表达形式转成下面形式

 

    {

        ‘home_owernship.OWN’: 0

        ‘home_owernship.MORTGAGE’: 0

        ‘home_owernship.RENT’: 1

    }

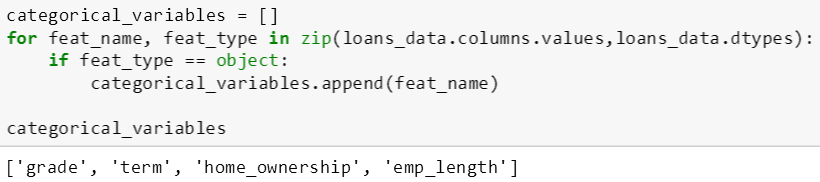
下面代码是找出 loans_data 里面所有非数值型特征值对应的特征，本例的四个特征都属于此类而被找出。

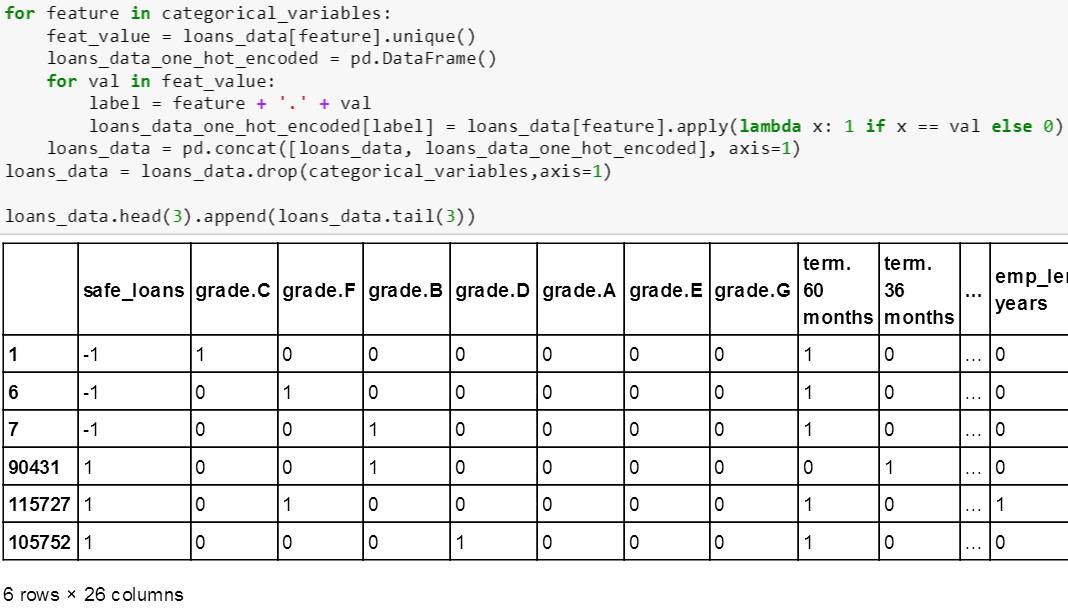
然后对每个特征做独热编码，用 drop() 函数将原来“分类字符型”特征那列删掉，而用 append() 函数将编码后的“数值型”特征加列。新的特征名称遵循以下起名惯例：

    新特征 = 老特征.老特征值

比如

    grade.C = grade.C

    term.60 months = term.60 months

而新特征值只能是 0 或 1。斯蒂文用以下惯例：

• 0 类分裂成左子树

• 1 类分裂成右子树

在独热编码之后，打印特征名字发现由原来 4 个特征增加到 26 个特征。

注：本章内容详情可参考 MM - decision tree 1, 2, 3 的 ipython notebook

第二章：决策树 (sklearn)

斯蒂文一开始直接使用 sklearn.tree 里面的模型，首先需要将上节处理好的数据以四比一的比例分成训练数据和验证数据，然后分别获取训练数据的输入值 X 和输出值 Y。

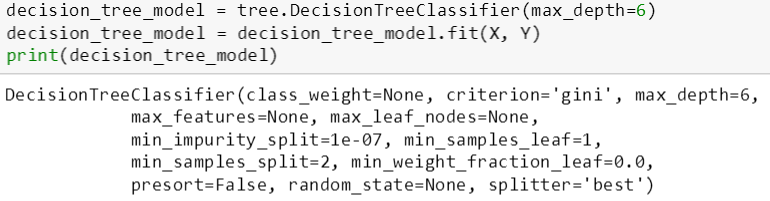
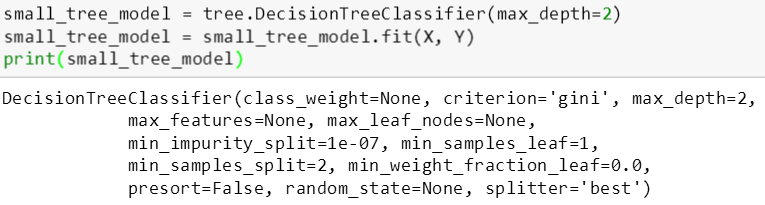
斯蒂文用 DecisionTreeClassifier 函数来建立两个树模型，最大树深 (max_depth) 分别是 6 层和 2 层，因此第一棵树 (适中树) 比第二棵树 (简单树) 复杂。然后用 fit() 函数来拟合 X 和 Y 生成树模型。从打印树的信息可看出，该模型用的是基尼指数 (gini) 来划分特征。

DecisionTreeClassifier 函数括号里的变量都可以赋予不同的值，斯蒂文此时就只想通过变化 max_depth 来控制树的复杂程度。

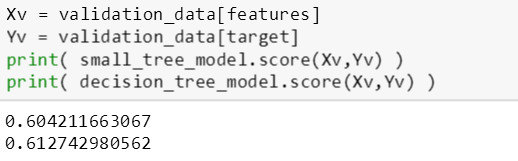
接下来看看这两棵树在训练数据和验证数据上的表现，即检查训练误差和验证误差：

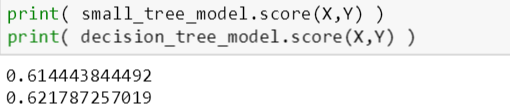
用 score() 函数来评估树的分类准确率，由上图可知，适中树比简单树的训练误差和验证误差低 (准确率高)。接下来用最大树深 10 层来生成一棵复杂树，如下：

复杂树的在训练数据和验证数据的准确率分别是 62.45% 和 60.78%，适中树的在训练数据和验证数据的准确率分别是 62.19% 和 61.27%，简单树的在训练数据和验证数据的准确率分别是 61.44% 和 60.42%。

当树由简单到复杂，训练准确率逐渐增高，而验证准确率先增高再降低。

    61.44% < 62.19% < 62.45%

    60.42% < 61.27% > 60.78%

这说明复杂树过拟合了，后面斯蒂文会用剪枝方法来避免树的过拟合。

注：本章内容详情可参考 MM - decision tree 1 的 ipython notebook

第三章：决策树 (MM)

直接用 sklearn 的 tree 模型固然好，但是毕竟是个黑箱子，但如果老板问一些模型实施细节原理，斯蒂文根本无法解释，为了保险起见，他自己也独立编写了一个树模型，用 MM 来表示，其中 MM 是 mean machine 的缩写。

3.1

子函数

编写树模型之间需要三个关键子函数，分别是：

1. 计算误分类个数

2. 选择最佳特征分裂

3. 创建树叶

计算误分类个数

count_num_mistakes 函数有一个输入变量：

• labels_in_node: 标签样例值 (数组)

其代码逻辑分两步：

1. 如果结点没有包含任何样本，返回 0；反之计算结点里面正例和反例的个数

2. 根据多数原则

1. 如果正例个数大于反例个数，那么反例是误分类则返回反例个数

2. 如果正例个数小于反例个数，那么正例是误分类则返回正例个数

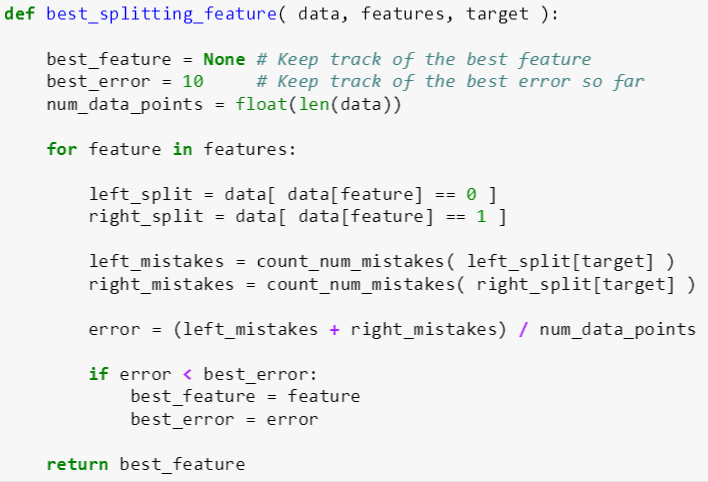
选择最佳特征分裂

best_splitting_feature 函数有三个输入变量：

• data: 某棵树 [数据表]

• features: 特征名称 [数组]

• target: 标签 [字符]

其代码逻辑分四步：

1. 初始化最佳特征和最佳误差率分别为 None 和 10
   

2. 对于每个特征 j，计算用其分裂的左子树和右子树的误分类数 (用 count_num_mistakes)，并计算总误分类率 j

3. 如果总误分类率 j 小于最佳误差率，那么最佳误差率为总误分类率 j，而最佳特征为特征 j

4. 重复运行第二、三步，最后返回最佳特征

创建树叶

create_leaf 函数有一个输入变量：

• target_values: 标签样例值 (数组)

其代码逻辑分三步：

1. 用字典类变量初始化 leaf，它的分裂特征为 None, 左子树为 None, 右子树为 None, 是否是叶子为 True 

2. 计算叶子中正例和反例的个数

3. 根据多数原则，赋值 leaf 的预测为 1 (正例个数大于反例个数)，-1 (反例个数大于正例个数)
   

3.2

构建决策树

创建树

利用上面三个子函数，斯蒂文可以很轻松的构建树模型，同时使用以下三个停止条件：

• 条件 1 - 某分支里所有样例都属于一类

• 条件 2 - 特征已经用完

• 条件 3 - 树的深度达到最大树深

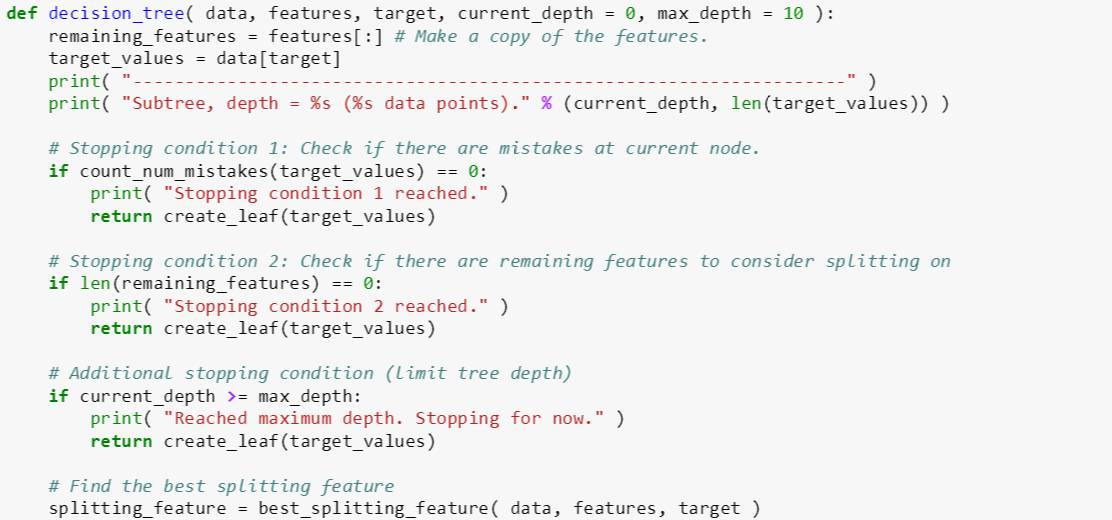
decision_tree 函数有五个输入变量：

• data: 某棵树 [数据表]

• features: 特征名称 [数组]

• target: 标签 [字符]

• current_depth: 当前树深 [整数]

• max_depth: 最大树深 [整数]

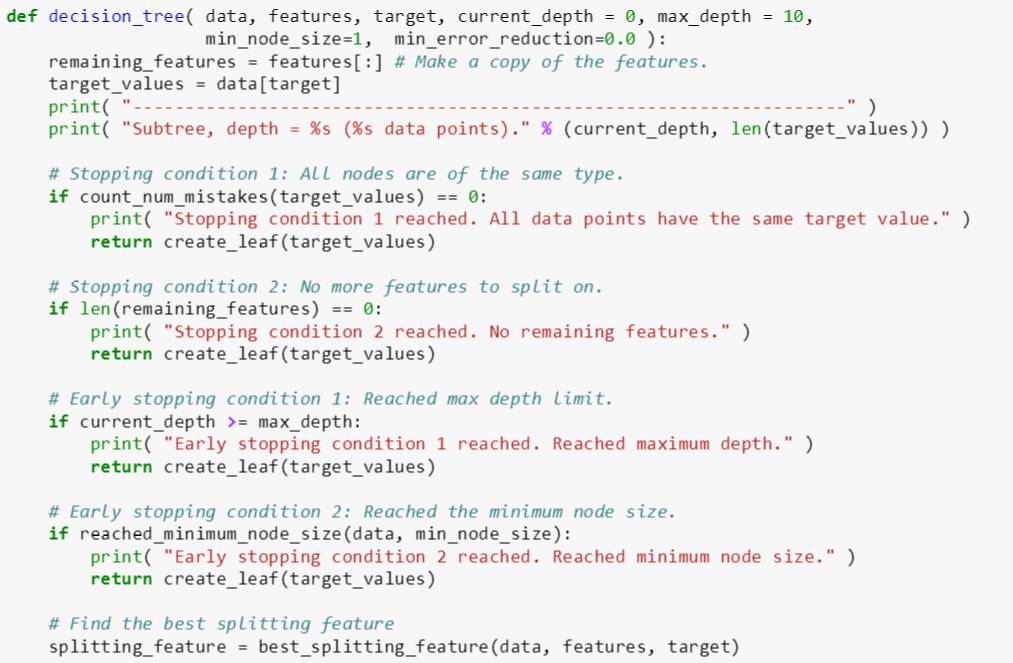
其代码逻辑分三步：

1. 创建 remaining_features 包含所有特征

2. 检查三种停止条件：

1. 如果误分类个数 (用 count_num_mistakes) 为 0，创建叶子 (停止条件 1)

2. 如果特征已用完，创建叶子 (停止条件 2)

3. 如果 current_depth 小于 max_depth，创建叶子 (停止条件 3)

3. 用 best_splitting_feature 找到最佳特征，并分裂成左子树和右子树，同时将最佳特征从 remaining_features 删除

1. 如果左子树或右子树所含样例个数等于父树所含样例个数，那么创建叶子

2. 反之，用递推方法继续用 decision_tree 来创建子树，这时 current_depth 在原来基础上加 1

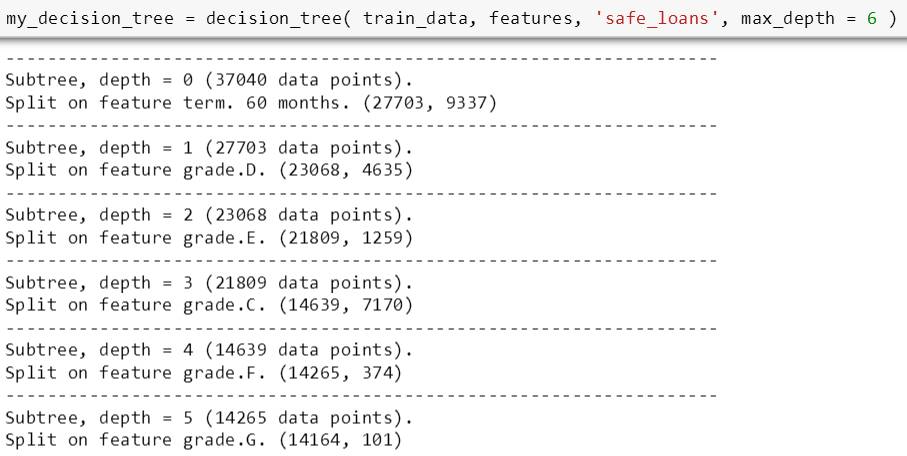
将 max_depth 设为 6，斯蒂文用上面程序训练了一棵树，每步分裂结果如下 (由于打印结果太长，只截屏了部分结果，详情可参考 MM - decision tree 2 的 ipython notebook) 

决策树预测

classify 函数有三个输入变量：

• tree: 树 (字典)

• x: 数据 (数据表)

• annotate: 注解 (布尔)
  

其代码逻辑为：

• 如果该树是叶子，返回叶子对应的预测类

• 如果该树不是叶子，找到其分裂特征值 f，递推返回

• classify(左子树) 如果 f = 0

• classify(右子树) 如果 f = 1

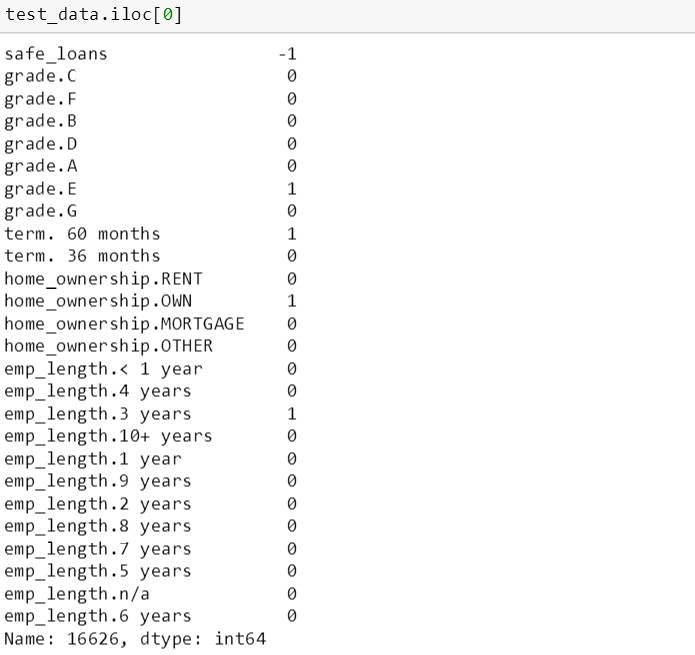
用上树来看看第一个测试数据上的分类结果，从下面信息看，这笔贷款是危险贷款 (safe_loans 的值为 -1)

用 classify 函数来看看分类结果，这棵树在 6 次分裂后预测它是恶性贷款。

由于 1 是代表右子树，0 是代表左子树，因此这个测试数据从根部先用“期限 60 个月”开始分裂到右子树，再用“评级 A”分裂到左子树，再用“评级 C”分裂到左子树，再用“评级 F”分裂到左子树，再用“评级 B”分裂到左子树，再用“评级 D”分裂到左子树，而它是片树叶，预测结果是 -1，恶性贷款。

决策树误差

misclassify_error 函数有两个输入变量：

• tree: 树 (字典)

• data: 数据 (数据表)

其代码逻辑为两步：

1. 用 apply 函数加上 classify 函数得到预测正例，并直接获取真实正例

2. 计算预测正例等于真实正例的个数，并返回误分类率

3.3

可视化决策树

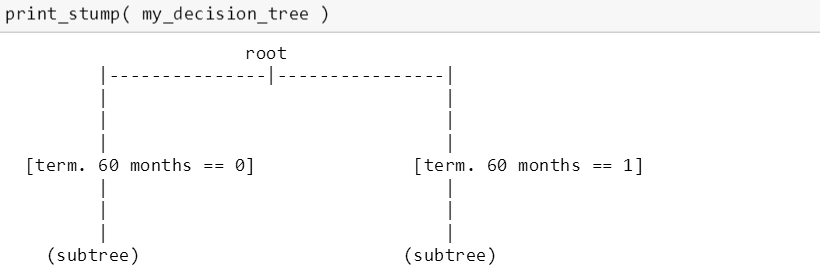
下面 print_stump() 函数是打印树桩的

由于打印出一棵完整的树有些难度，斯蒂文从根部一层层的打印树桩。下图显示从根部用“期限 60 个月”来做分裂的。

在左子树上，用“评级 D”来做分裂。

在左子树的左子树上，用“评级 E”来做分裂。

在左子树的右子树上，发现已经是片树叶，因此无需再分裂。

在右子树上，用“评级 A”来做分裂。

在右子树的右子树上，用“工作年数 n/a”来做分裂，emp_length.n/a 代表着工作年数那栏没填，也就是说借贷人没有工作。

在右子树的左子树上，用“评级 C”来做分裂，我们发现分裂后左边还是一棵树，但右边已经是一片叶子，无需分裂了。

用 print_stump 函数可以一步步把整棵树从根到叶完整的勾画出来。

注：本章内容详情可参考 MM - decision tree 2 的 ipython notebook

第四章：决策树 (Pruning)

第二章里面用 sklearn 自带的 DecisionTreeClassifier 加上 max_depth 为 10 的模型造成了对数据的过拟合。从决策树一贴可知，预修剪和后修剪都可以避免过拟合。斯蒂文决定用预修剪，在决策树生成过程中，对每个结点在划分前先进行估计，一旦遇到以下三个提前停止条件 (early stopping condition)，就应该将当前结点标记为叶结点。

• 提前停止条件 1：当树的深度超过最大树深
  

• 提前停止条件 2：当内结点包含的数据个数小于一个特定值

• 提前停止条件 3：当继续分裂不能减小分类误差率

4.1

子函数

编写树模型并预修剪需要五个关键子函数 (其中前三个在上章已完成)，分别是：

1. 计算误分类个数

2. 选择最佳特征分裂

3. 创建树叶

4. 判断到达节点包含数据的最小个数
   

5. 计算分裂前后误差减小值

判断到达节点包含数据的最小个数

该函数有两个输入变量：

• data: 某棵树 [数据表]

• min_node_size: 不允许继续分裂的节点包含数据的最小个数 [正整数]，比如某节点有 15 个数据，但是 min_node_size 是 20，因此这个节点不继续做分裂而称为叶节点。

如果 data 的个数小于 min_node_size，返回 true 值，反之返回 false 值。该函数用于预修剪中的提前停止条件 2。

计算分裂前后误差减小值

该函数有两个输入变量：

• error_before_split: 分裂前的分类误差

• error_after_split: 分裂后的分类误差

该函数返回分裂前后的分类误差的差值，用于预修剪中的提前停止条件 3。

3.2

构建决策树

下面 decision_tree 函数是上章的加强版，主要考虑了提前停止条件 2 和 3。

decision_tree 函数有七个输入变量：

• data: 某棵树 [数据表]

• features: 特征名称 [数组]

• target: 标签 [字符]

• current_depth: 当前树深 [整数]

• max_depth: 最大树深 [整数]

• min_node_size: 某个节点不允许继续分裂的节点包含数据的最小个数 [正整数]

• min_error_reduction: 最小误差减小值 [实数]

其代码逻辑分三步：

1. 创建 remaining_features 包含所有特征

2. 检查三种停止条件和三种提前停止条件：

1. 如果误分类个数 (用 count_num_mistakes) 为 0，创建叶子 (停止条件 1)

2. 如果特征已用完，创建叶子 (停止条件 2)

3. 如果 current_depth 小于 max_depth，创建叶子 (停止条件 3)

4. 提前停止条件 1 和停止条件 3 一样

5. 如果 reached_minimum_node_size 返回值小于 min_node_size，创建叶子 (提前停止条件 2)

6. 用 best_splitting_feature 找到最佳特征，并分裂成左子树和右子树，如果 error_reduction 返回值小于 min_error_reduction，创建叶子 (提前停止条件 3)。同时将最佳特征从 remaining_features 删除

3. 用递推方法继续用 decision_tree 来创建子树，这时 current_depth 在原来基础上加 1

接着斯蒂文用上面程序训练了两棵树 (新树和老树)，它们的区别是 min_node_size (100 和 0) 和 min_error_reduction (0 和 -1)，很明显新树不容易过拟合，因为它允许叶节点包含的数据个数是 100 个，而且不允许分裂后的误差小于 0 (即不允许分裂后误差增大)。

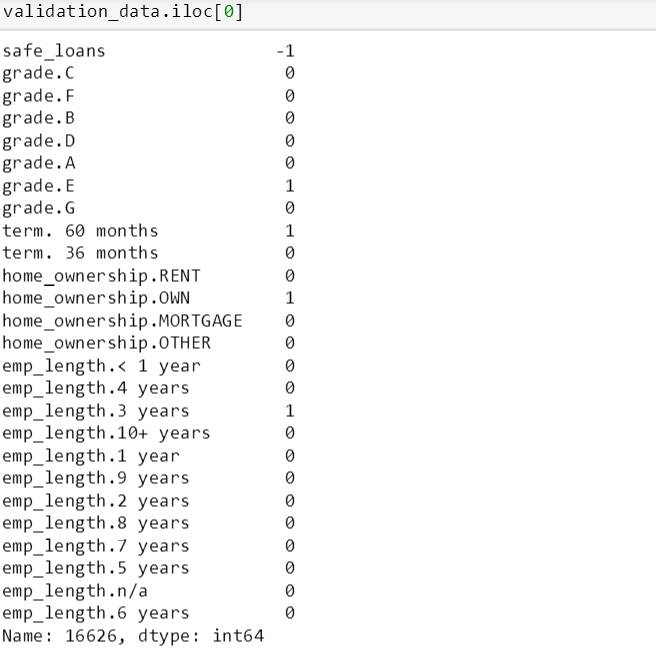
训练完之后来看看两棵树在第一个验证数据上的分类结果，从下面信息看，这笔贷款是危险贷款 (safe_loans 的值为 -1)

用上一章 classify 函数来看看分类结果，很明显新树只需要 2 次分裂就能到达叶节点来预测这笔贷款是恶性贷款；而老树需要 6 次分裂才能预测它是恶性贷款。

由上可知，两棵树都能准确的预测贷款类型，现在用两棵树来计算测试误差，新树的误差 0.3909 小于老树的误差 0.3915，由此看出适当的修剪来防止树的过拟合可以提高预测准确率的。

3.2

探索决策树

最后斯蒂文需要找到一个合适的没有过拟合的模型，那么他需要探索合适的最大树深，合适的最小误差减小值和合适的节点包含数据最小个数。在探索之前还需要一个用来衡量树的复杂度的子函数，如下：

一般来说，树越复杂，它的叶子数也就越多。count_leaves 函数的输入变量是一棵树上，如果这棵树是叶子，那么返回 1 代表着一片叶子；如果不是叶子，那么用递推方式将 count_leaves 函数作用在它的左子树和右子树上。

探索最大树深

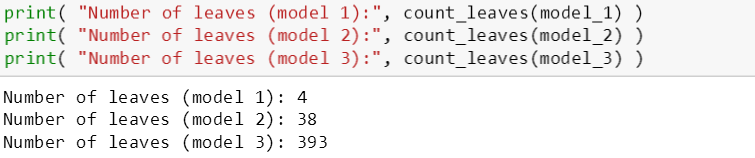
为了探索最大树深，斯蒂文建立了树模型 1, 2, 3:

• 模型 1: max_depth = 2, 树深太浅

• 模型 2: max_depth = 6, 树深正好

• 模型 3: max_depth = 14, 树深太深

模型中 min_node_size 和 min_error_reduction 都是一样的， 因此斯蒂文想排除其他控制“过拟合”参数，而只关注 max_depth 对树的影响。

从模型 1 到 3，它们的复杂度是递增的，由下图可知它们的训练误差是递减的 (符合逻辑)，但是模型 3 的验证误差比模型 2 的大，这说明模型 3 过拟合了数据。

接下来看出三个模型含叶子树，发现模型 1 只含有 4 片叶子，太过于少；而模型 3 含有 393 片叶子，太过于多；模型 2 正好，而且对应的验证误差最小。

探索最小误差减小值

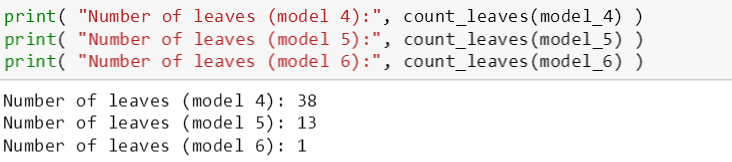
为了探索最小误差减小值，斯蒂文建立了树模型 4, 5, 6:

• 模型 4: min_error_reduction = -1, 不会提前停止

• 模型 5: min_error_reduction = 0, 正好提前停止

• 模型 6: min_error_reduction = 5, 总是提前停止

模型中 max_depth 和 min_node_size 都是一样的， 因此斯蒂文想排除其他控制“过拟合”参数，而只关注 min_error_reduction 对树的影响。

模型 4 和 5 的验证误差相似 (模型 6 的验证误差相比太大)，但是它们的叶子数分别是 38 和 13，由此看出模型 4 比模型 5 要复杂。

因此模型 5 胜过模型 4，因为它比模型 4 简单而且预测能力和模型 4 不相上下。

探索节点包含数据最小个数

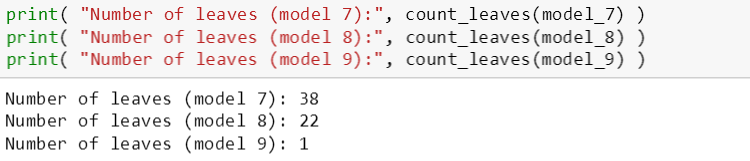
为了探索节点包含数据最小个数，斯蒂文构建了树模型 7, 8, 9:

• 模型 7: min_node_size = 0, 个数太少

• 模型 8: min_node_size = 2000, 个数正好

• 模型 9: min_node_size = 50000, 个数太多

模型中 max_depth 和 min_error_reduction 都是一样的， 因此斯蒂文想排除其他控制“过拟合”参数，而只关注 min_node_size 对树的影响。

模型 7 和 8 的验证误差相似 (模型 9 的验证误差相比太大)，但是它们的叶子数分别是 38 和 22，由此看出模型 7 比模型 8 要复杂。

因此模型 8 胜过模型 7，因为它比模型 7 简单而且预测能力和模型 7 不相上下。

注：本章内容详情可参考 MM - decision tree 3 的 ipython notebook

下帖会用 boosting 技巧来继续研究 lending club 的贷款分类问题。 Stay Tuned！