【经典书】矩阵流形优化算法，237页pdf，普林斯顿大学出版社

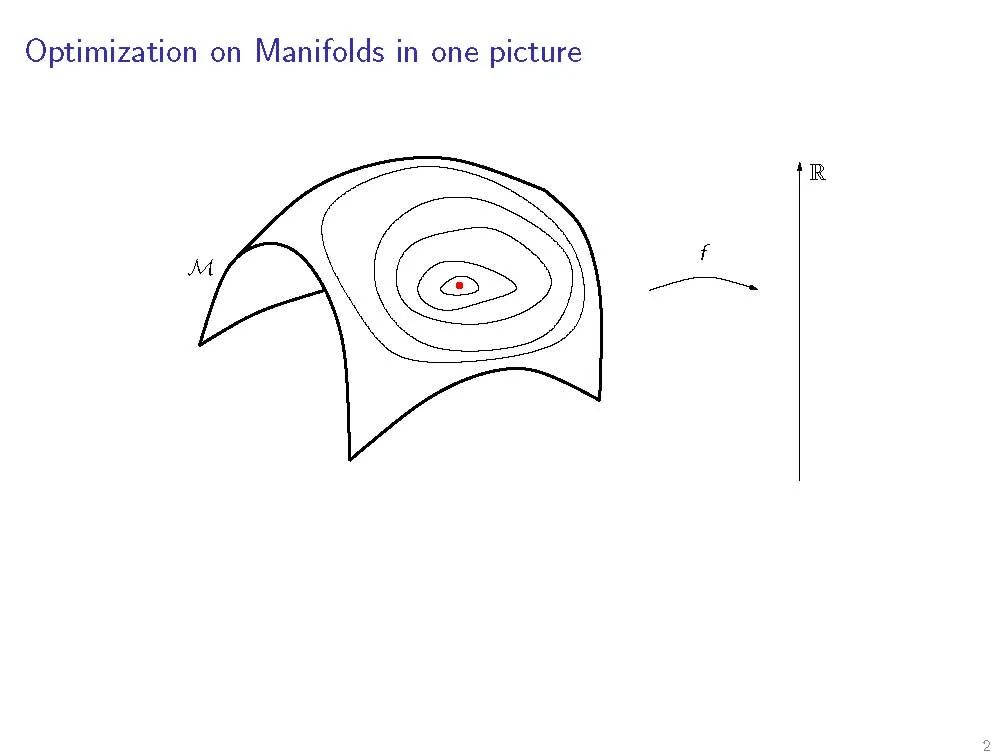
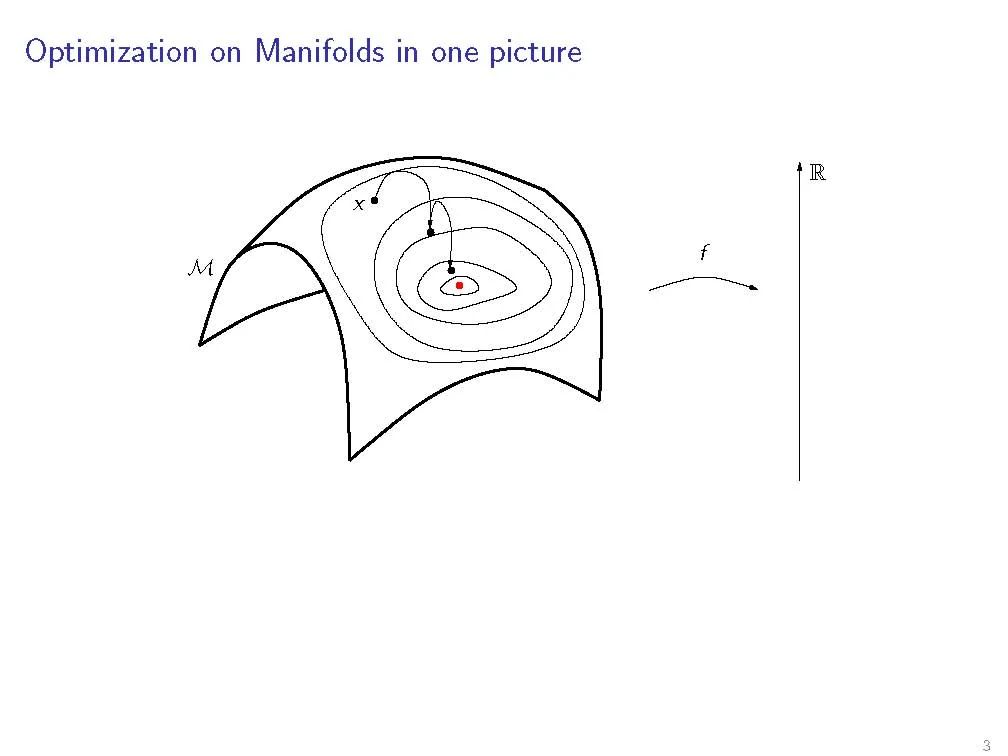
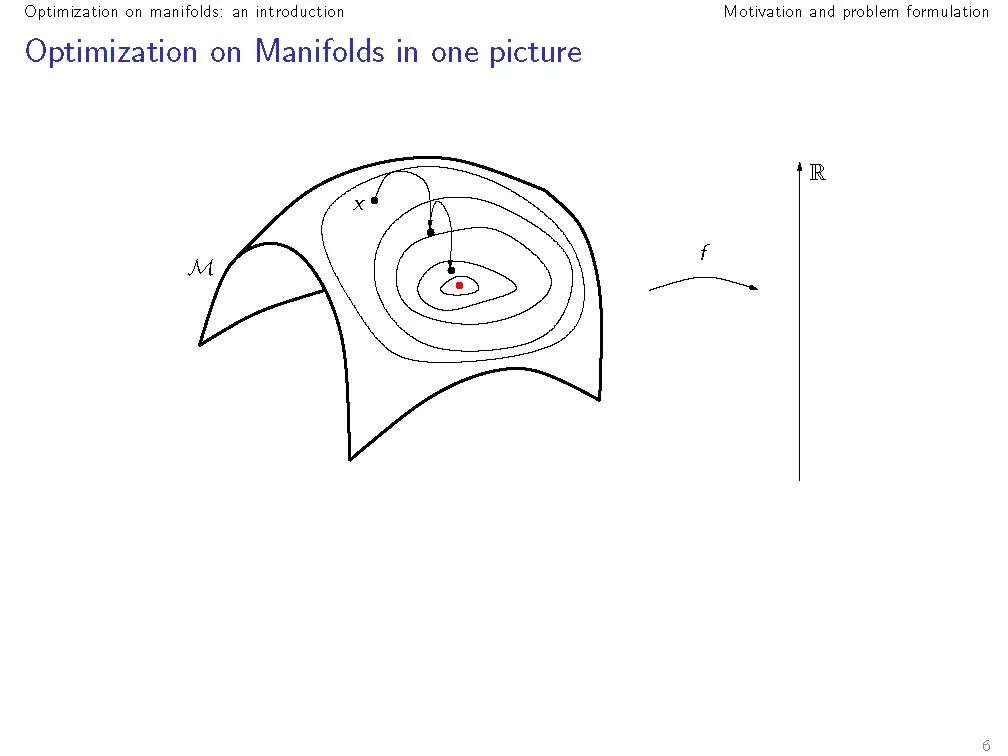
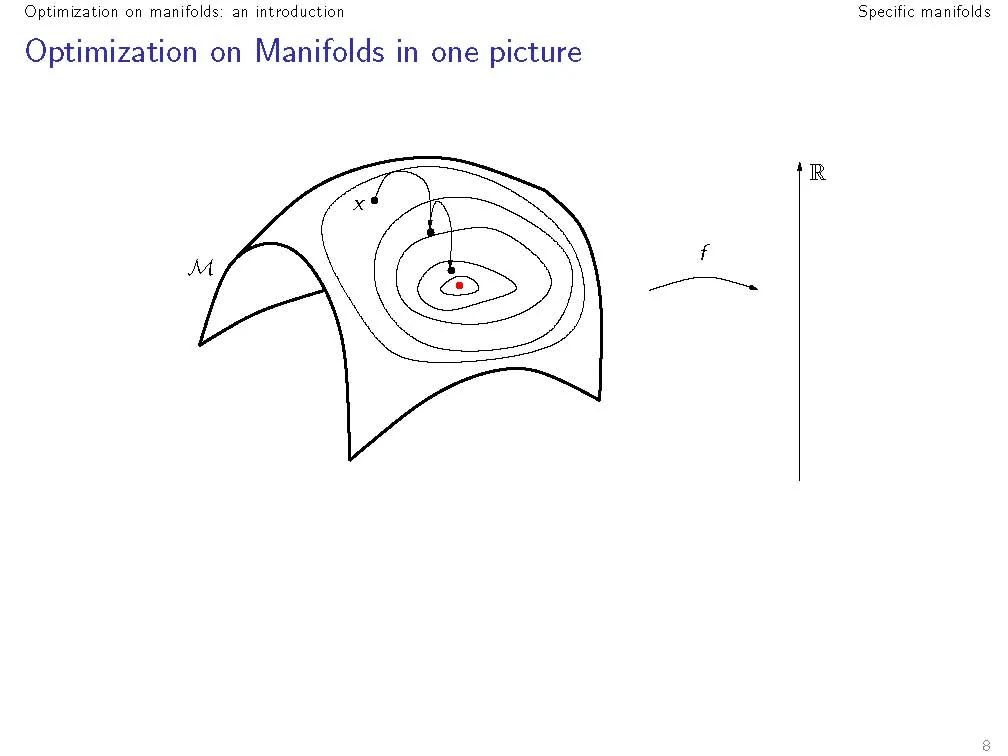
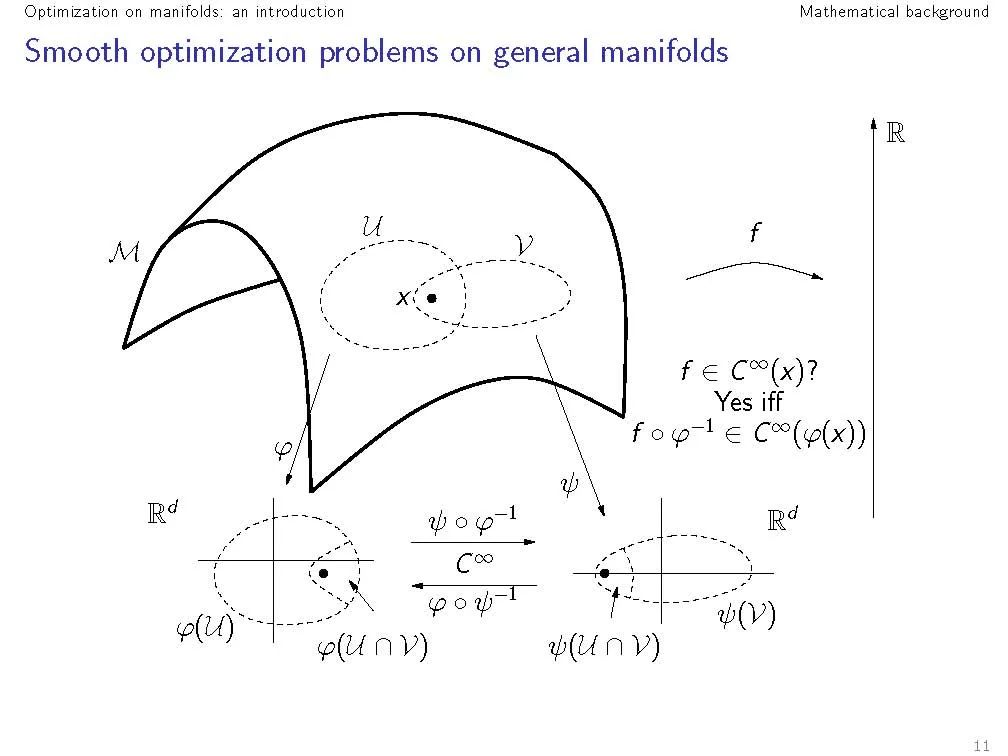
科学和工程中的许多问题都可以换种说法，即具有流形结构的矩阵搜索空间的优化问题。这本书展示了如何利用这些问题的特殊结构来开发有效的数值算法。它是应用数学家和计算机科学家感兴趣的。

科学和工程中的许多问题都可以换种说法，即具有流形结构的矩阵搜索空间的优化问题。这本书展示了如何利用这些问题的特殊结构来开发有效的数值算法。它把重点放在了算法的数值公式和它的微分几何抽象上——说明好的算法是如何从微分几何、优化和数值分析的洞察力中同等地得出的。另外两个理论章节为读者提供了算法发展所必需的微分几何背景。在其他章节中，几个著名的优化方法，如最速下降法和共轭梯度法被推广到抽象流形。这本书提供了这些方法中的每一个的一般发展，建立在几何章节的材料上。然后，它指导读者通过计算，把这些几何公式的方法变成具体的数值算法。在数值线性代数中特征空间问题的选择问题中，所给出的最先进的算法与现有的最佳算法是有竞争力的。

矩阵流形上的优化算法提供了在线性代数、信号处理、数据挖掘、计算机视觉和统计分析中广泛应用的技术。它可以作为研究生水平的教科书，对应用数学家、工程师和计算机科学家感兴趣。

Optimization Algorithms on Matrix Manifolds

https://sites.uclouvain.be/absil/amsbook/

专知便捷查看

便捷下载，请关注专知公众号（点击上方蓝色专知关注）

• 后台回复“M237” 就可以获取《【经典书】矩阵流形优化算法，237页pdf，普林斯顿大学出版社》专知下载链接

专知，专业可信的人工智能知识分发，让认知协作更快更好！欢迎注册登录专知www.zhuanzhi.ai，获取5000+AI主题干货知识资料！

欢迎微信扫一扫加入专知人工智能知识星球群，获取最新AI专业干货知识教程资料和与专家交流咨询！

点击“ 阅读原文 ”，了解使用 专知 ，查看获取5000+AI主题知识资源