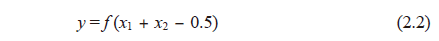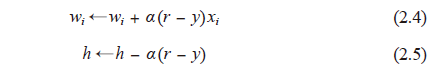理解神经网络——图解深度学习

2018 年 7 月 13 日 遇见数学

下文节选自图灵《图解深度学习》，已获出版社授权，【遇见数学】特此表示感谢！

在神经网络的发展历程中，出现过几次蓬勃发展的时期。在此期间，人们提出了多层感知器和误差反向传播等方法。要想理解深度学习，就必须掌握这些基本方法。本章首先会介绍神经网络的历史，然后对神经网络的具体内容及误差反向传播算法进行说明。

2.1　神经网络的历史

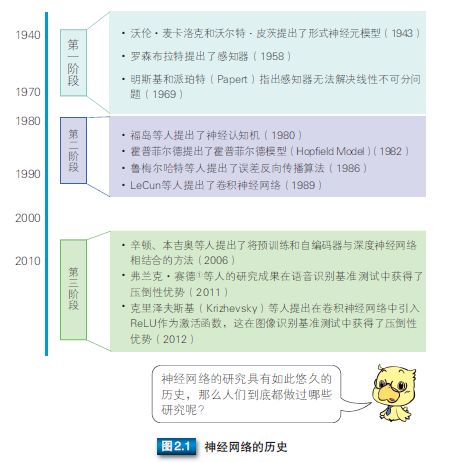
深度学习是基于神经网络发展起来的技术，而神经网络的发展具有悠久的历史，且发展历程可谓一波三折。如今，历经两次潮起潮落后，神经网络迎来了它的第三次崛起。图 2.1 展示了其发展历程中的转折点。通过此图还可以看出，人们对神经网络的研究可以追溯到 20 世纪 40 年代，并且第一次热潮持续到了 20 世纪 60 年代末。1943 年，美国神经生理学家沃伦•麦卡洛克（Warren McCulloch）和数学家沃尔特•皮茨（Walter Pitts）对生物神经元进行建模，首次提出了一种形式神经元模型 [43]。这个神经元模型通过电阻等元件构建的物理网络得以实现，被称为 M-P 模型。1958 年，罗森布拉特（Roseblatt）又提出了感知器，这意味着经过训练后，计算机能够确定神经元的连接权重。就这样，神经网络的研究迎来了第一次热潮 [55]。然而在 1969 年，明斯基（Minsky）等人指出感知器无法解决线性不可分问题，使得神经网络的研究陷入了低潮 [44]。

①　即 Frank Seide，现任微软亚洲研究院主管研究员。——译者注

这一时期面临的主要问题是感知器无法解决逻辑异或运算这样的线性不可分问题。这个问题可以通过多层感知器解决，但是当时人们还不清楚如何进行分层训练。20 世纪 80 年代，鲁梅尔哈特（Rumelhart）等人提出了误差反向传播算法（Back Propagation，BP）[58]，通过设置多层感知器，解决了线性不可分问题。同一时期，福岛 ① 等人提出了神经认知机 ②，神经认知机模拟了生物的视觉传导通路 [16] ；LeCun ③ 等人将相当于生物初级视皮层的卷积层引入到神经网络中，提出了卷积神经网络 [35, 36]。使用误差反向传播算法虽然能够进行分层训练，但是仍然存在一些问题，比如训练时间过长，只能根据经验设定参数，没有预防过拟合的理论依据 [62]，再加上当时支持向量机（Support Vector Machine， SVM）等方法备受瞩目，因此神经网络的研究再次陷入了低潮。

尽管神经网络的研究陷入低潮，但辛顿（Hinton）[22, 25, 26, 47, 60] 和本杰奥（Bengio）[3, 4, 18, 56] 等人并未停止研究，继续为神经网络的发展打基础。得益于他们的研究成果，自 2011 年起，神经网络就在语音识别和图像识别基准测试中获得了压倒性优势，自此迎来了它的第三次崛起。而且由于卷积神经网络的结构非常适合用于识别图像，再结合那些研究成果，所以也重新受到了人们的重视。与第二次崛起时不同的是，在这个时期，硬件已得到了进一步发展，大量训练数据的收集也更加容易。在硬件方面，通过高速的 GPU 并行运算，只需几天即可完成深层网络（例如 10 层网络）的训练。另外，随着互联网的普及，我们能够获得大量的训练数据，进而抑制过拟合。这些外界环境的变化也为神经网络的技术进步提供了有力支撑。

从下一节开始，我们将按顺序介绍这个历史背景下的神经网络。

①　即福岛邦彦（Kunihiko Fukushima），日本京都大学博士毕业，现为 Fuzzy LogicSystems Institute 特别研究员。——编者注②　Neocognitron，也有“新认知机”的译法，本书统一采用“神经认知机”这个译词。——译者注③　即 Yann LeCun，现任 Facebook AI 研究院院长，被称为卷积神经网络之父。他本人曾于 2017 年 3 月在清华大学演讲时公布自己的中文名为杨立昆。——编者注

2.2　M-P模型

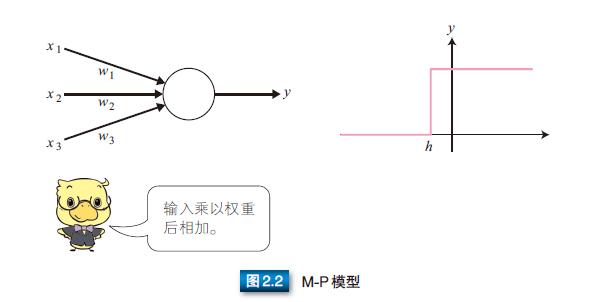
M-P 模型是首个通过模仿神经元而形成的模型 [43]。如图 2.2 所示，在 M-P 模型中，多个输入节点 {xi | i = 1, ..., n} 对应一个输出节点 y。每个输入 xi 乘以相应的连接权重 wi，然后相加得到输出 y。结果之和如果大于阈值 h，则输出 1，否则输出 0。输入和输出均是 0 或 1。

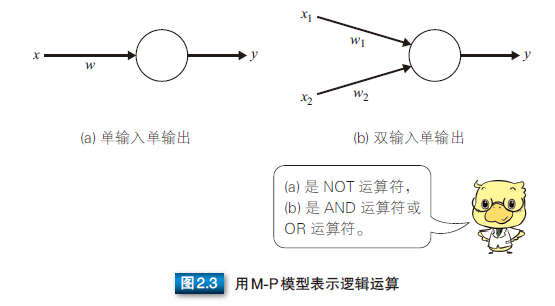
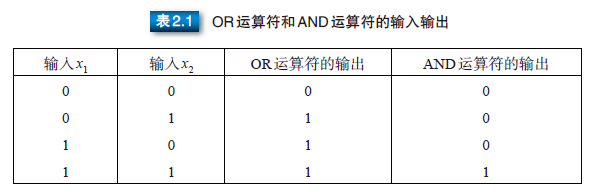
M-P 模型可以表示 AND 和 OR 等逻辑运算。如图 2.3 所示，M-P模型在表示各种逻辑运算时，可以转化为单输入单输出或双输入单输出的模型。

取反运算符（NOT 运算符）可以使用图 2.3(a) 所示的单输入单输出的M-P 模型来表示。使用取反运算符时，如果输入 0 则输出 1，输入 1 则输出 0，把它们代入 M-P 模型的公式 (2.1)，可以得到 wi =－2, h =－1。

逻辑或（OR 运算符）和逻辑与（AND 运算符）可以使用图 2.3(b) 所示的双输入单输出 M-P 模型来表示。各运算符的输入与输出的关系如表 2.1 所示。根据表中关系，以 OR 运算为例时，公式 (2.1)中的 wi 和 h 分别为 w1 = 1, w2 = 1, h = 0.5，把它们代入公式 (2.1) 可以得到下式。

以 AND 运算为例时，w1 = 1, w2 = 1, h = 1.5，把它们代入公式 (2.1) 可以得到下式。

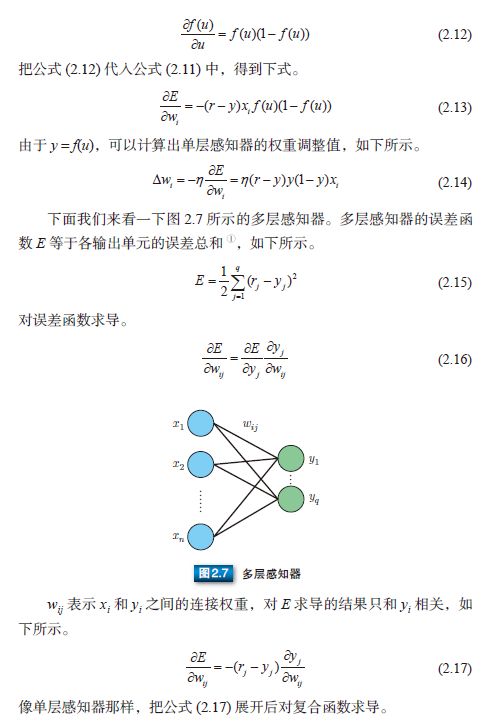
由此可见，使用 M-P 模型可以进行逻辑运算。但是，上述的 wi 和h 是如何确定的呢？当时还没有通过对训练样本进行训练来确定参数的方法，只能人为事先计算后确定。此外，M-P 模型已通过电阻得到了物理实现。

向上滑动阅览简介及目录

图解深度学习

作者：[日]山下隆义

当当广告

购买

图灵程序设计丛书出版年：2018年5月本书特色:

1.实用
136张图+60段代码帮助理解相关理论和工具的使用方法。可作为专业理论书籍、参考文献的辅助读物随时翻阅

2.专业
浓缩深度学习的关键知识点，内容涉及神经网络、卷积神经网络、受限玻尔兹曼机、自编码器、泛化能力的提高等。同时辅以代码，介绍了Theano、Pylearn2、Caffe、DIGITS、Chainer和TensorFlow等深度学习工具的安装和使用方法。
3.易懂
图文并茂，知识点清晰直观、便于理解。全彩印刷、版式精美，技术书也可赏心悦目。

前言

第1章　绪论

第2章　神经网络

第3章　卷积神经网络

第4章　受限玻尔兹曼机

第5章　自编码器

第6章　提高泛化能力的方法

第7章　深度学习工具

第8章　深度学习的现在和未来

参考文献

2.3　感知器

2.2 节中的逻辑运算符比较简单，还可以人为事先确定参数，但逻辑运算符 wi 和 h 的组合并不仅仅限于前面提到的这几种。罗森布拉特提出的感知器能够根据训练样本自动获取样本的组合 [55]。与 M-P 模型需要人为确定参数不同，感知器能够通过训练自动确定参数。训练方式为有监督学习，即需要设定训练样本和期望输出，然后调整实际输出和期望输出之差的方式（误差修正学习）。误差修正学习可用公式 (2.4) 和(2.5) 表示。

α 是确定连接权重调整值的参数。α 增大则误差修正速度增加，α 减小则误差修正速度降低 ①。

感知器中调整权重的基本思路如下所示。

• 实际输出 y 与期望输出 r 相等时，wi 和 h 不变

• 实际输出 y 与期望输出 r 不相等时，调整 wi 和 h 的值参数 wi 和 h 的调整包括下面这两种情况。

1 . 实际输出 y = 0、期望输出 r = 1 时（未激活）

• 减小h

• 增大xi = 1 的连接权重wi

• xi = 0 的连接权重不变

2 . 实际输出y = 1、期望输出r = 0 时（激活过度）

• 增大h

• 降低xi = 1 的连接权重wi

• xi = 0 的连接权重不变

训练过程如下所示。

①　α 可以看作是学习率，用于控制调整速度，太大会影响训练的稳定性，太小则使训练的收敛速度变慢。——译者注

因为感知器会利用随机数来初始化各项参数，所以训练得到的参数可能并不相同。

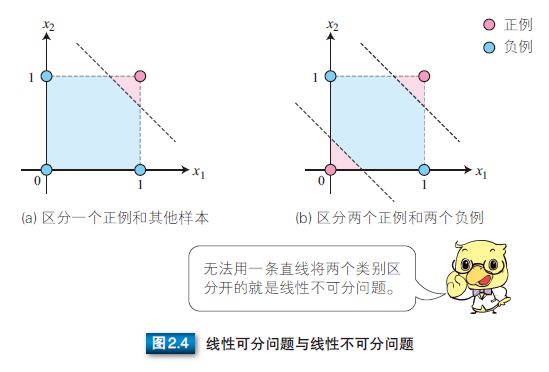
使用误差修正学习[21]，我们可以自动获取参数，这是感知器引发的一场巨大变革。但是，感知器训练只能解决如图2.4(a) 所示的线性可分问题，不能解决如图2.4(b) 所示的线性不可分问题。为了解决线性不可分问题，我们需要使用多层感知器。

2.4　多层感知器

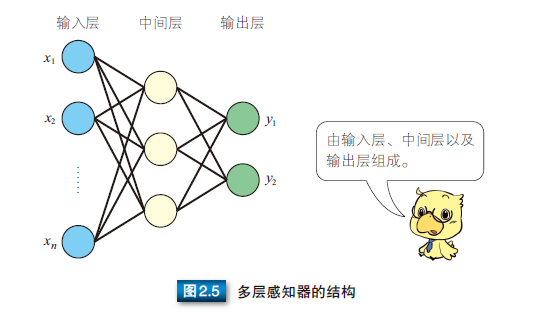
为了解决线性不可分等更复杂的问题，人们提出了多层感知器（multilayer perceptron）模型。如图 2.5 所示，多层感知器指的是由多层结构的感知器递阶组成的输入值向前传播的网络，也被称为前馈网络或正向传播网络。

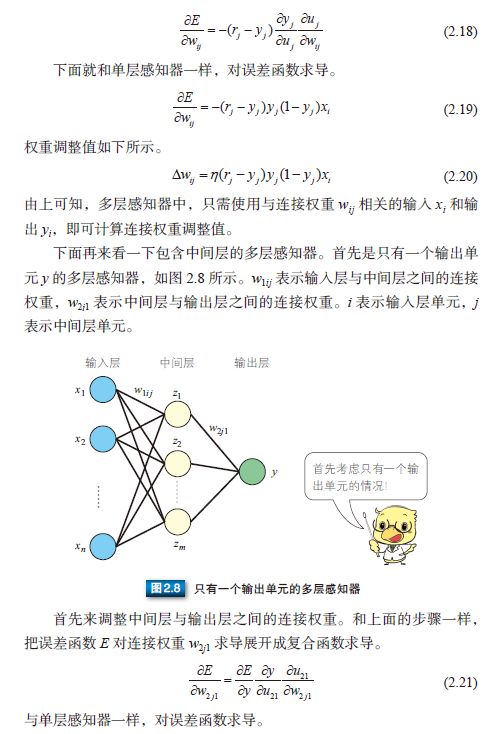
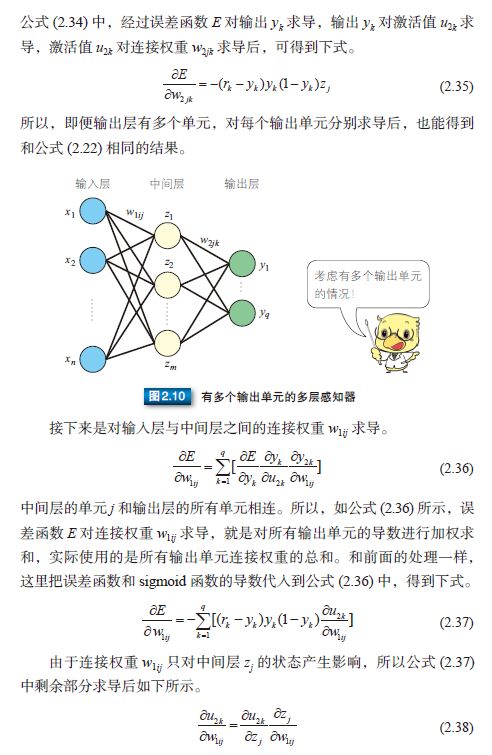
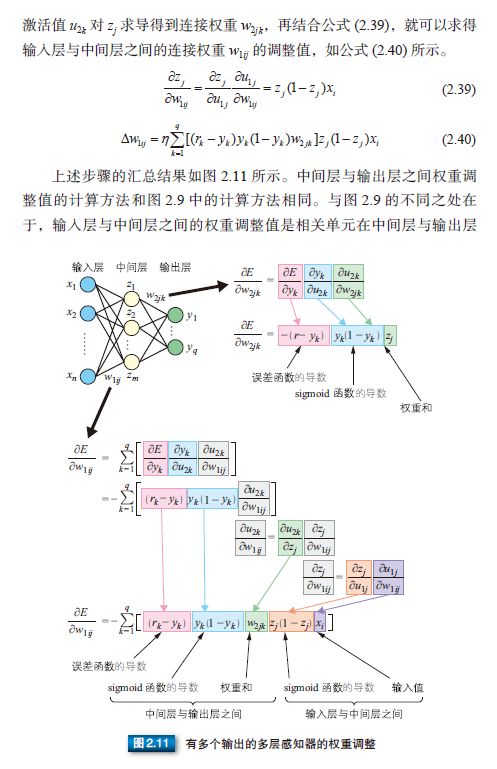
多层感知器通常采用三层结构，由输入层、中间层及输出层组成。与公式 (2.1) 中的 M-P 模型相同，中间层的感知器通过权重与输入层的各单元（unit）相连接，通过阈值函数计算中间层各单元的输出值。中间层与输出层之间同样是通过权重相连接。那么，如何确定各层之间的连接权重呢？单层感知器是通过误差修正学习确定输入层与输出层之间的连接权重的。同样地，多层感知器也可以通过误差修正学习确定两层之间的连接权重。误差修正学习是根据输入数据的期望输出和实际输出之间的误差来调整连接权重，但是不能跨层调整，所以无法进行多层训练。因此，初期的多层感知器使用随机数确定输入层与中间层之间的连接权重，只对中间层与输出层之间的连接权重进行误差修正学习。所以，就会出现输入数据虽然不同，但是中间层的输出值却相同，以至于无法准确分类的情况。那么，多层网络中应该如何训练连接权重呢？人们提出了误差反向传播算法。

2.5　误差反向传播算法

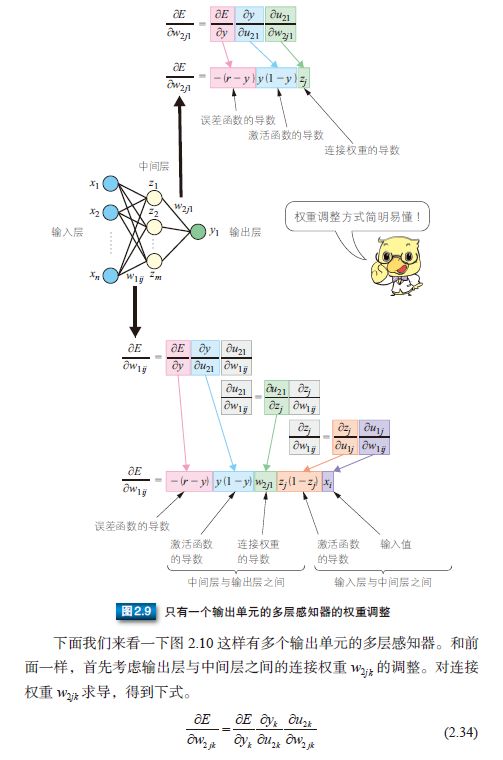
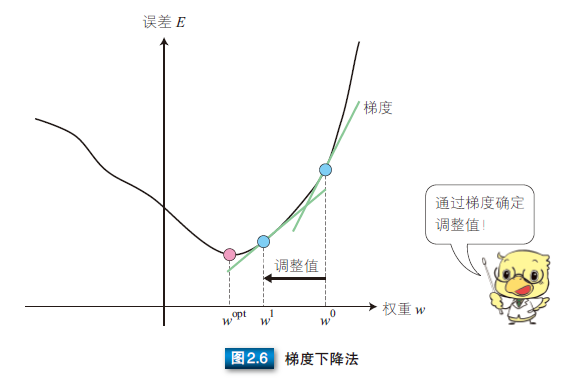
多层感知器中，输入数据从输入层输入，经过中间层，最终从输出层输出。因此，误差反向传播算法 [57] 就是通过比较实际输出和期望输出得到误差信号，把误差信号从输出层逐层向前传播得到各层的误差信号，再通过调整各层的连接权重以减小误差。权重的调整主要使用梯度下降法（gradient descent method）。如图 2.6 所示，通过实际输出和期望输出之间的误差 E 和梯度，确定连接权重 w0 的调整值，得到新的连接权重 w1。然后像这样不断地调整权重以使误差达到最小，从中学习得到最优的连接权重 wopt。这就是梯度下降法。

下面我们就来看看误差和权重调整值的计算方法。计算误差可以使用最小二乘误差函数（参照公式 (2.43)）。通过期望输出 r 和网络的实际输出 y 计算最小二乘误差函数 E。E 趋近于 0，表示实际输出与期望输出更加接近。所以，多层感知器的训练过程就是不断调整连接权重 w，以使最小二乘误差函数趋近于 0。

接着再来看一下权重调整值。根据上述说明，权重需要进行调整以使最小二乘误差函数趋近于 0。对误差函数求导就能得到图 2.6 中给定点的梯度，即可在误差大时增大调整值，误差小时减小调整值，所以连接权重调整值 Δw 可以用公式 (2.6) 表示。