研究发现拓扑狄拉克节线量子态诱发表面电声耦合反常增强现象
最近,中国科学院金属研究所沈阳材料科学国家研究中心材料设计与计算研究部的研究人员及合作者发现了金属铍表面的巨大电声耦合的反常增强是其块体材料中拓扑狄拉克节线量子态诱发的。因为该节线态会导致鼓膜类拓扑表面态,它们在表面费米能级附近局域,增高了态密度,尤其是通过与低频区表面声子的耦合诱发了巨大的电声耦合效应。研究团队也在其它拓扑材料中揭示了类似的效应。相关成果发表于《物理评论快报》(Phys. Rev. Lett. 123, 136802 (2019))并入选(PRL Editor’s suggestion),作为亮点文章(highlighted article)在PRL网站推荐。
电声相互作用在材料和凝聚态物理中是普遍存在的,也是固体物理量子机制理论中研究最为普遍的内容之一。它通常反映的是固体材料中原子在平衡位置振动对电子结构的影响,因此电声相互作用对材料的许多性质有重要影响。比如,它不但影响材料随温度变化的电子能带结构,导致光电子能谱、拉曼和中子实验中经常观察到的典型扭结或者Kohn异常现象,而且它还会加强金属随温度变化的电阻,增加半导体材料的载流子迁移速率,更会对传统BCS超导的产生起到决定性作用等。因电声相互作用耦合了晶格和自旋自由度或者可调节色心自旋的寿命,在自旋电子学和量子信息领域内也有重要应用。
金属的电声耦合效应通常不会很大,比如块体金属铍的电声耦合效应只有0.24。但铍(0001)表面的电声耦合效应竟然出现反常增强,是其块体的5倍以上。这种反常增强现象自上世纪90年代起就被多种不同实验观测到,迄今为止这一现象的机理未明,并引起了广泛争议。
对于金属铍表面电声耦合机理的研究,最大的困难之一是电声耦合基本参数——伊利艾伯格函数的精确求算。尽管以前的研究在频率区间内积分伊利艾伯格函数得出的电声耦合强度数值与实验相近,但计算结果并不可靠。主要因为以前理论获得的相应频率区间的计算结果与实验结果存在严重偏差,同时也无法给出与微观机理相关的数据。为了解决这一问题,金属所研究团队首先发展了高精度的第一性原理计算算法,通过巧妙的数学处理拆解伊利艾伯格函数,将其在频率区间的分布与积分变换到电子及声子的动量空间,从而率先观测到了每个电子及声子动量对电声耦合的影响。为了验证算法,他们构建了金属铍表面的薄膜模型,计算不但获得了与实验结果相符的伊利艾伯格函数分布,严格修正了以往与实验严重偏离的结果,而且还为量化每个电子及声子动量对电声耦合的贡献提供了分析工具。
使用研究团队改进后的精确算法和工具,计算量化了电子动量空间下的伊利艾伯格函数,发现金属铍狄拉克节线量子态引发的鼓膜类拓扑非平庸表面态对其电声耦合的贡献占比超过了80%,这一发现澄清了长期以来广受争议的金属铍表面电声耦合反常增强的机理,同时也揭示了其它拓扑材料中存在相似的效应。审稿专家评价该工作的意义认为:“这些研究者正在刷新寻找改进量子计算和模拟并具有量子相干性的材料的科学(包括物理)。”另一位审稿人认为:“我认为这些新结果难以置信的引人入胜,作者提供了清晰的证据表明表面电声耦合效应的反常增强来源于其体拓扑根源。”
该工作由金属所研究员陈星秋、特别研究助理李荣汉(共同一作)和博士生李江旭(共同一作)等共同完成,得到国家杰出青年科学基金和沈阳材料科学国家研究中心等支持。这个工作也是研究团队继两年前率先报道在铍、镁、钙和锶金属中拓扑狄拉克节线量子态后的又一重要进展。
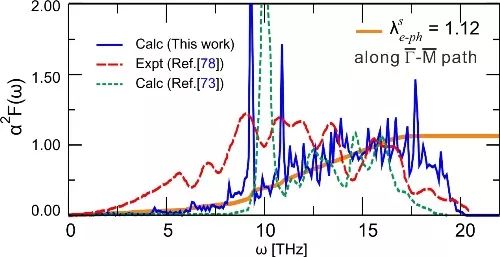
图1 改进后的算法提高了伊利艾伯格函数的求算精度。比如沿着Be(0001)表面的G-M路径积分的伊利艾伯格函数在频率区间内的峰与实验配备良好。
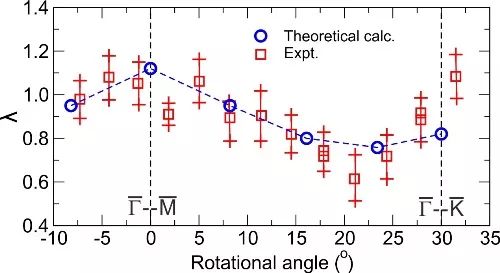
图2 计算精确阐述了金属铍的(0001)表面电声耦合的各向异性,与实验测试结果一致。
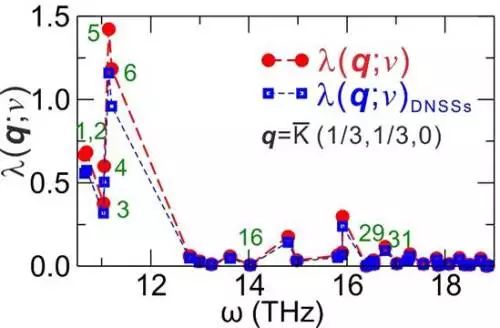
图3 计算揭示了金属铍的(0001)表面来自狄拉克节线诱导的鼓膜拓扑态电子与低频区表面声子耦合导致电声耦合的反常增强。图示非平庸表面态电子与低频区K点表面声子的耦合显著贡献了反常增强现象。
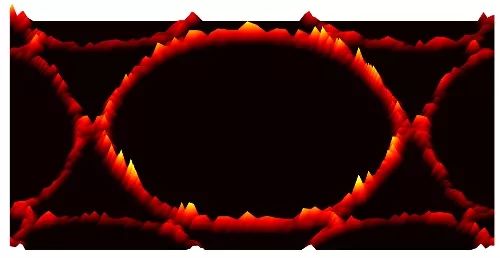
图4 对应于非平庸鼓膜类拓扑表面局域电子态引发的各向异性电声耦合反常增强局域峰。
来源:中国科学院金属研究所
温馨提示:近期,微信公众号信息流改版。每个用户可以设置 常读订阅号,这些订阅号将以大卡片的形式展示。因此,如果不想错过“中科院之声”的文章,你一定要进行以下操作:进入“中科院之声”公众号 → 点击右上角的 ··· 菜单 → 选择「设为星标」