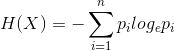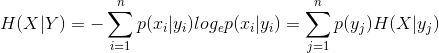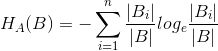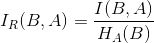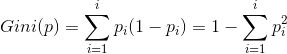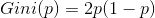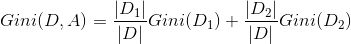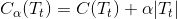决策树算法

注：图片来自网络

分享嘉宾：张道甜 算法工程师

编辑整理：Hoh Xil

内容来源：作者授权

出品社区：DataFun

注：欢迎转载，转载请注明出处

——决策树算法——

决策树算法可以实现分类算法、回归算法，计算复杂度不高，对缺失值不太敏感，同时可以处理不相关特征；同时是集成学习算法 Random Forest 的基础算法。

——决策树类型——

1. ID3：解决分类问题

❶ 分裂节点：计算信息增益，值最大的为当前分裂特征

信息论中定义为互信息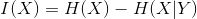：，信息增益越大，当前节点该特征越适合做分裂特征。

熵的理解：特征的取值越多，其信息熵越大

X 代表特征，n 为特征 X 的不同取值的数量，Pi 是取第 i 个值的概率；

条件熵：在 Y 条件下，X 的熵

信息增益：

❷ ID3算法的不足

• 没有考虑过拟合问题
  

• 没有考虑缺失值

• 信息增益为分裂标准，容易偏向于取值较多的特征

• 没有考虑连续特征变量 ( 但可通过连续特征离散化处理 )

针对 ID3 的不足，出现了 C4.5 算法.

2. C4.5：解决分类问题

❶ 分裂节点：计算信息增益的增益率，即该特征的信息增益与特征熵的比值，值最大的为当前节点的分裂特征。

特征熵：

信息增益比：

样本特征 A 的特征值越多，则分母 ( 特征熵 ) 越大，分裂节点可以避免偏向特征值较多的特征。

B 为样本集合，A 为样本的特征，n 为特征 A 的类别数，Bi 为特征 A 第 i 个取值对应的样本数，|B| 为样本数；

❷ C4.5 的优点：

• 采用信息增益比，解决了 ID3 信息增益偏向于取值较多的特征的问题

• 考虑了 ID3 没有解决连续属性离散化问题

  e.g. 某样本中特征 A 为连续特征值，根据 A 的所有取值，从小到大排序，分别取出所有相邻两个值的均值，记做集合 m，然后计算 m 中的每个值当做二元分类点的信息增益，选择信息增益最大的值为连续特征 A 的二元分类点。

• 缺失值的自动处理策略

• C4.5 引入了正则化系数进行初步剪枝

❸ C4.5 的不足：

• 只能用于分类

• 剪枝方法有优化空间

• 生成的是多叉树，但使用二叉树会比多叉树效率更高

• 选择了复杂度较高的熵来度量，计算比较耗时，且遇到连续值还需要进行排序

3. CART 树：可以解决分类和回归问题

❶ 分裂节点的选择：

CART 树选取特征是根据基尼系数，基尼系数越小，模型的不纯度越小。ID3、C4.5 都是基于熵的运存，会涉及大量的对数运算，为了解决这个问题，CART 树用基尼系数作为分裂特征选取标准，首先我们理解一下基尼系数：

在分类问题中：如果一个数据集有 i 个类别，第 i 个类别的概率 Pi，那么基尼系数为：

则二分类的基尼系数：

在分裂节点中，如果一个样本集合选取 A 特征的某个值，将数据集分为 D1、D2 两部分，那么数据集在 A 特征下的基尼系数为：

同时针对 CART 树，一方面选取了基尼系数作为特征选取的衡量标准，另一方面采用的是二叉树而不是多叉树，那么在运算效率上就会有很大的提高。

❷ CART 分类树对连续值的特征变量离散化

CART 分类树在处理连续特征变量与 C4.5 的处理方式是一样的，唯一区别就是选取划分点时的度量值不同。

e.g. 某样本中特征 A 为连续特征值，根据 A 的所有取值，从小到大排序，分别取出所有相邻两个值的均值，记做集合 m，然后计算 m 中的每个值当做二元分类点时的基尼系数，选择基尼系数最小的值为连续特征 A 的二元分类点。可以将小于这个点的分类为 A 类，大于这个点的分类为 B 类，这样就将连续变量离散化了。

❸ CART 回归树对连续值的特征变量离散化

采用的是和方差的度量方法：

e.g. 某样本中特征 A 为连续特征值，根据 A 的所有取值，从小到大排序，分别取出所有相邻两个值的均值，记做集合 m，当二元分类点 x 将数据分成了 s1、s2 两个集合，则针对两个数据集合，分别计算均方差，最后求和，那么和方差最小的为当前特征的划分点。

❹ NOTE：CART 树是一个二叉树，ID3、C4.5 是多叉树

e.g. 在分类问题上：某数据集上有特征 A，有 A1,A2,A3 共三个类别，那么在 ID3、C4.5 算法中，会建立成三个分支。但是在 CART 分类树中，会将 A1,A2,A3 划分成 {A1，A2} 和 {A3}、{A1} 和 {A2，A3}、{A2} 和 {A1,A3}，分别计算基尼系数，最小的一组为当前节点特征 A 的分裂依据，同时特征 A 还有机会参与以后的节点建立，这是与 ID3、C4.5 不同的地方。

❺ CART 回归和分类树对结果预测的区别

CART 回归树预测结果是根据叶子节点的中位数或均值作为预测结果，而 CART 分类树是根据叶节点的类别概率最大的作为预测结果。

❻ CART 树剪枝

决策树算法会出现过拟合现象，那么为了提高了模型的泛化能力，降低过拟合，CART 树提供了剪枝的方法。剪枝的方法有预剪枝和后剪枝，CART 树采用的是后剪枝的方法。剪枝的过程会产生很多剪之后的树，那么我们采用交叉验证的方法评测各个剪枝效果，选出效果最好的树作为最终的模型。

CART 回归树和 CART 分类树的剪枝过程是一样的，只是在损失函数上的度量方式不一样，一个是使用基尼系数，另一个是使用均方差。

损失函数的度量：

在剪枝过程中，对任意一棵子树 T_t，其损失函数为：

其中，α 为正则化参数，C(T_t) 为训练数据的误差 ( CART 回归树用的是均方差，CART 分类树是基尼系数 )，|T_t| 为叶子节点的数量。

当 α=0 时，则原生的 CART 树是最优的子树；

当 α=∞ 时，则 CART 树的根节点组成的单节点树为最优子树

当 α 越大，剪枝的越厉害，其剪枝的后的树越小。

剪枝思路：

当位于节点 t 的任意一颗子树 T_t，没有剪枝的情况下，其损失：

当剪枝到根节点，即只保留根节点，其损失是：

当 α=0 或者很小时，则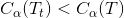：，当增大到一定程度时：

所以当 T 和 T_t 满足 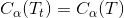，即：

就可以对 T_t 进行剪枝，将子节点全部剪掉，剩下一个叶子结点 T。

最后要做的就是交叉验证，当我们计算出所有节点是否剪枝的 α，将 α 对应的最优子树在训练集上进行交叉验证，找到最优子树作为最终结果。

以上是我对 CART 树的理解，谢谢大家。

原文地址：

https://blog.csdn.net/weixin_39948381/article/details/90601931

文章作者

张道甜，算法工程师，某公司的智能评估定价算法体系负责人。

——END——

文章推荐：

腾讯信息流内容理解技术实践

解密商业化广告投放平台技术架构

DataFun：

专注于大数据、人工智能领域的知识分享平台。

一个「在看」，一段时光！👇