【专知-Deeplearning4j深度学习教程02】用ND4J自己动手实现RBM: 图文+代码

会员服务 ·

【专知-Deeplearning4j深度学习教程02】用ND4J自己动手实现RBM: 图文+代码

2017 年 10 月 13 日 专知 Hujun

点击上方“专知”关注获取更多AI知识!

【导读】主题链路知识是我们专知的核心功能之一，为用户提供AI领域系统性的知识学习服务，一站式学习人工智能的知识，包含人工智能（机器学习、自然语言处理、计算机视觉等）、大数据、编程语言、系统架构。使用请访问专知进行主题搜索查看 - 桌面电脑访问www.zhuanzhi.ai, 手机端访问www.zhuanzhi.ai 或关注微信公众号后台回复" 专知"进入专知，搜索主题查看。继Pytorch教程后，我们推出面向Java程序员的深度学习教程DeepLearning4J。Deeplearning4j的案例和资料很少，官方的doc文件也非常简陋，基本上所有的类和函数的都没有解释。为此，我们推出来自中科院自动化所专知小组博士生Hujun创作的-分布式Java开源深度学习框架Deeplearning4j学习教程，第二篇，用ND4J自己动手实现RBM。

Deeplearning4j开发环境配置
ND4J（DL4J的矩阵运算库）教程
基于DL4J的CNN、AutoEncoder、RNN、Word2Vec等模型的实现

本文主要讲解Deeplearning4j的矩阵运算库ND4J的使用，考虑到这是第二篇教程，因此还介绍了DL4J配置等内容，全文组织如下：

Deeplearning4j的配置
ND4J简介及接口简介
RBM（受限玻尔兹曼机）简介
自己动手用ND4J实现RBM

配置Deeplearning4j

对于有N卡且希望使用GPU的开发者，请先安装Cuda8.0或Cuda7.5，希望在CPU上运行DL4J的可忽略此步骤。接下来，在Maven工程的pom.xml中加入下面依赖：

<dependency>
    <groupId>org.nd4j</groupId>    <!-- CPU版 -->
    <artifactId>nd4j-native</artifactId>    <!-- cuda7.5 GPU版 -->
    <artifactId>nd4j-cuda-7.5</artifactId>    <!-- cuda8.0 GPU版 -->
    <artifactId>nd4j-cuda-8.0</artifactId>
    <version>版本号</version>
</dependency>

<dependency>
    <groupId>org.deeplearning4j</groupId>
    <artifactId>deeplearning4j-core</artifactId>
    <version>版本号</version>
</dependency>

<dependency>
    <groupId>org.slf4j</groupId>
    <artifactId>slf4j-log4j12</artifactId>
    <version>版本号</version>
</dependency>

注意： 先根据自己的需求（CPU/CUDA7.5/CUDA8.0）修改下面依赖中nd4j的类型，并将各依赖的版本号修改为需要的版本号，最新的版本号可在Maven中央仓库里查看：

ND4J:

CUDA 7.5: https://mvnrepository.com/artifact/org.nd4j/nd4j-cuda-7.5
CUDA 8.0: https://mvnrepository.com/artifact/org.nd4j/nd4j-cuda-8.0
CPU: https://mvnrepository.com/artifact/org.nd4j/nd4j-native
GPU:

DL4J: https://mvnrepository.com/artifact/org.deeplearning4j/deeplearning4j-core
slf4j-log4j12 : https://mvnrepository.com/artifact/org.slf4j/slf4j-log4j12

最后，在Maven工程的src/main/resources中添加log4j.properties文件，否则会导致DL4J在训练时不显示监听信息等情况。

# Root logger option log4j.rootLogger=INFO, stdout # Direct log messages to stdout log4j.appender.stdout=org.apache.log4j.ConsoleAppender log4j.appender.stdout.Target=System.out log4j.appender.stdout.layout=org.apache.log4j.PatternLayout log4j.appender.stdout.layout.ConversionPattern=%d{yyyy-MM-dd HH:mm:ss} %-5p %c{1}:%L - %m%n

配置完成，开始享受Deeplearning4j。

ND4J简介

ND4J是深度学习框架Deeplearning4j的矩阵运算框架，Python的Numpy类似。ND4J不仅可以在CPU上运行，也可以在GPU上运行，具有较好的运算效率。

下面列出一些ND4J常用操作：

随机产生矩阵

//创建一个shape为[3,5]的随机矩阵INDArray data = Nd4j.rand(new int[]{3,5});System.out.println(data);

输出：

[[0.91,  0.19,  0.50,  0.53,  0.33],   [0.35,  0.13,  0.92,  0.62,  0.69],   [0.79,  0.30,  0.12,  0.81,  0.88]]

根据数组生成矩阵

double[] arrayData = new double[]{3,4,5,1,2,5};INDArray data = Nd4j.create(arrayData, new int[]{3,2});System.out.println(data);

输出：

[[3.00,  4.00],   [5.00,  1.00],   [2.00,  5.00]]

获取矩阵维度和形状

INDArray data = Nd4j.rand(new int[]{3,2});int[] shape = data.shape();System.out.println("dimension:" + shape.length);System.out.println("shape: " + Arrays.toString(shape));

输出：

dimension:2 shape: [3, 2]

矩阵乘法

INDArray data = Nd4j.rand(new int[]{3,2});System.out.println("data:\n" + data);//矩阵乘实数INDArray mulResult = data.mul(5);System.out.println("data * 5:\n" + mulResult);//data和data的转置相乘INDArray mmulResult = data.mmul(data.transpose());System.out.println("data.dot(data.T):\n" + mmulResult);//data和data元素级相乘（等价于每个元素进行平方）INDArray elementWiseMulResult = data.mul(data);System.out.println("data * data:\n" + elementWiseMulResult);

输出：

data: [[0.59,  0.50],   [0.55,  0.66],   [0.41,  0.68]] data * 5: [[2.97,  2.50],   [2.74,  3.32],   [2.03,  3.40]] data.dot(data.T): [[0.60,  0.66,  0.58],   [0.66,  0.74,  0.67],   [0.58,  0.67,  0.63]] data * data: [[0.35,  0.25],   [0.30,  0.44],   [0.16,  0.46]]

关于ND4J的详细教程可查看ND4J官网的一个教程：http://nd4j.org/userguide。下面，我们用ND4J来自己实现一个RBM（受限玻尔兹曼机）。

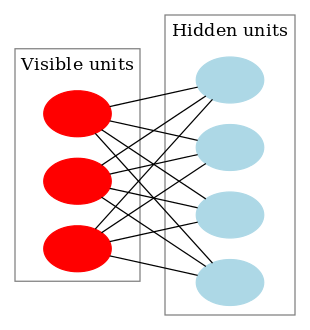
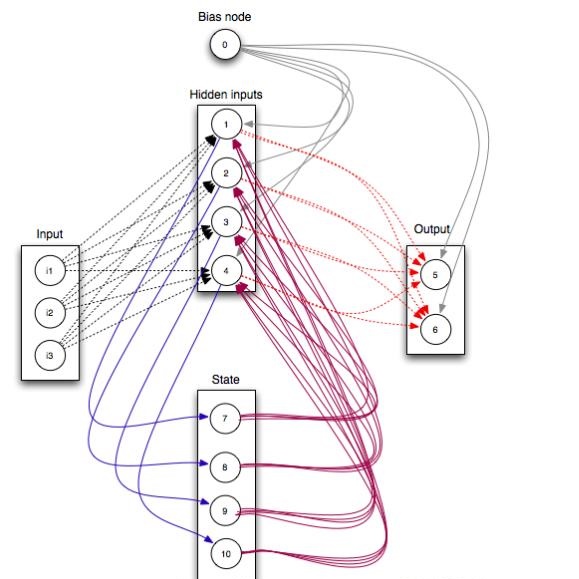
RBM（受限玻尔兹曼机）简介

RBM是一个神经网络，只有一个可见层和一个隐藏层。这里不详细介绍RBM，想了解的可以查看维基百科：

https://en.wikipedia.org/wiki/Restricted_Boltzmann_machine。简而言之，RBM的作用，就是可以无监督地学习到2个变换，第一个变换可以将输入数据的特征向量v转换为一个新的特征向量h，另一个变换可以将h还原为v。很多情况下，h比v对分类器更友好，即h是学习到的更好的特征。

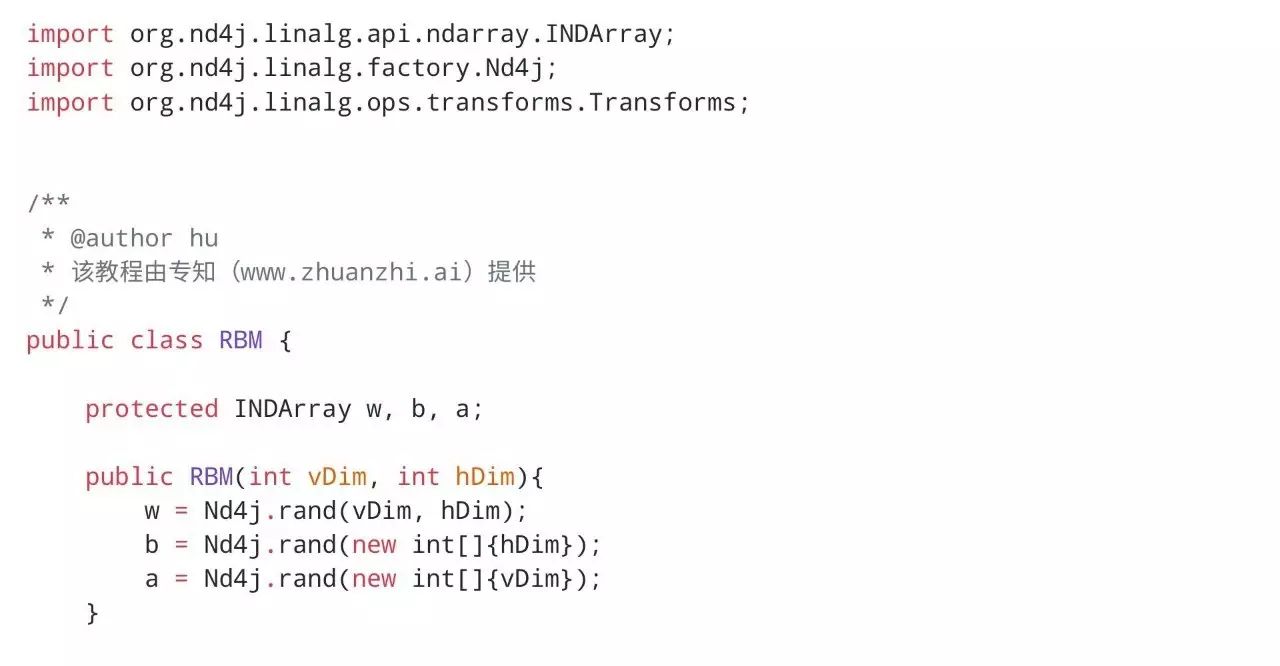
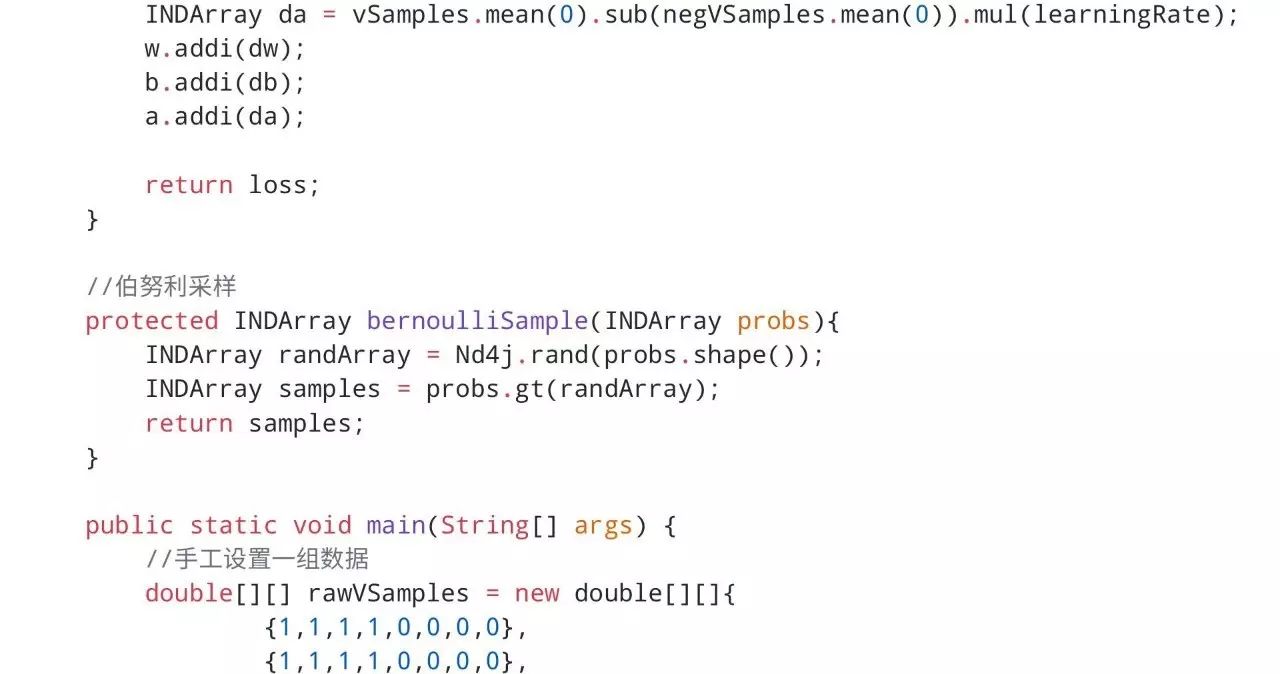
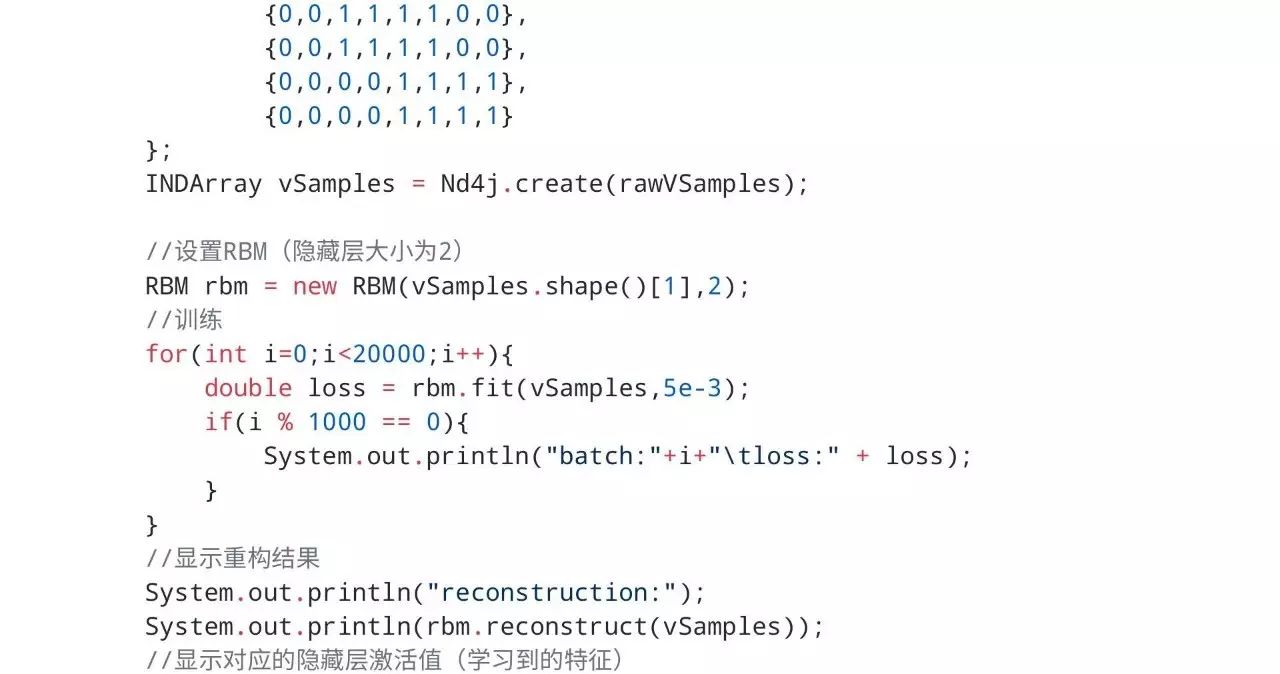
用ND4J实现RBM

下面代码中相关的公式可在维基百科的RBM词条中查看。考虑到手机微信浏览器可能会出现代码展示不全的情况，我们将完整工程上传到了https://github.com/CrawlScript/RBM4j

运行结果：

reconstruction: [[0.00,  1.00,  1.00,  1.00,  0.00,  0.00,  0.00,  0.00],   [1.00,  1.00,  1.00,  1.00,  0.00,  0.00,  0.00,  0.00],   [0.00,  0.00,  1.00,  1.00,  1.00,  1.00,  0.00,  0.00],   [0.00,  0.00,  1.00,  1.00,  1.00,  1.00,  0.00,  1.00],   [0.00,  0.00,  0.00,  0.00,  1.00,  1.00,  1.00,  1.00],   [0.00,  0.00,  0.00,  0.00,  1.00,  1.00,  1.00,  1.00]] features: [[0.00,  1.00],   [0.00,  1.00],   [1.00,  1.00],   [1.00,  1.00],   [1.00,  0.00],   [1.00,  0.00]]

可以看出，RBM完美地重构了输入数据，并且学到了更好的低维特征。

明天请继续关注“DeepLearning4j”教程。

完整系列搜索查看，请PC登录

www.zhuanzhi.ai, 搜索“DeepLearning4j”即可得。

对DeepLearning4j教程感兴趣的同学，欢迎进入我们的专知DeepLearning4j主题群一起交流、学习、讨论，扫一扫如下群二维码即可进入：