机器学习------令人头疼的正则化项

监督机器学习问题无非就是在规则化参数的同时最小化误差。最小化误差是为了让模型拟合训练数据，而规则化参数是防止模型过分拟合训练数据，但训练误差小并不是最终目标，最终目标是希望模型的测试误差小，也就是能准确的预测新的样本。所以需要保证模型“简单”的基础上最小化训练误差，这样得到的参数才具有好的泛化性能(也就是测试误差也小)，而模型“简单”就是通过规则函数来实现的。

一般来说，监督学习可以看做最小化下面的目标函数：

（正则化代价函数）=（经验代价函数）+（正则化参数）X（正则化项）

第一项是衡量模型预测与实际的误差，因为要拟合训练样本，所以要求这一项最小，也就是要求模型尽量的拟合训练数据。但不仅要保证训练误差最小，更希望模型测试误差小，所以需要加上第二项去约束模型尽量的简单。

机器学习的大部分带参模型都和这个型很相似。其实大部分就是变换这两项。对于第一项Loss函数，如果是Square loss，那就是最小二乘了；如果是Hinge Loss，那就是著名的SVM了；如果是Exp-Loss，那就是 Boosting了；如果是log-Loss，那就是Logistic Regression了，等等。不同的loss函数，具有不同的拟合特性，这个也得就具体问题具体分析的。

L0范数

L0范数是指向量中非0的元素的个数。如果用L0范数来规则化一个参数矩阵W的话，就是希望W的大部分元素都是0，换句话说，让参数W是稀疏的。

但是一般稀疏都会想到L1范数，所以我来讲讲L1范数。

L1范数

L1范数是指向量中各个元素绝对值之和，也叫“稀疏规则算子”（Lasso Regularization）。

L1范数会使权值稀疏？

因为它是L0范数的最优凸近似。实际上，任何的规则化算子，如果它在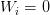的地方不可微，并且可以分解为一个“求和”的形式，那么这个规则化算子就可以实现稀疏。这说是这么说，W的L1范数是绝对值，|w|在w=0处是不可微，但这还是不够直观，所以需要和L2范数进行对比分析。

既然L0可以实现稀疏，为什么不用L0，而要用L1呢？

原因：一是因为L0范数很难优化求解（NP难问题），二是L1范数是L0范数的最优凸近似，而且它比L0范数要容易优化求解。

L2范数

L2范数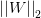：，在回归里面，它的回归叫“岭回归”（Ridge Regression），也叫它“权值衰减weight decay”。这用的很多，因为它的强大功效是改善机器学习里面一个非常重要的问题：过拟合。至于过拟合是什么，自己查查（O(∩_∩)O~~，很简单的知识点）。通俗的讲就是应试能力很强，实际应用能力很差。例如下图所示（来自Ng的course）：

为什么L2范数可以防止过拟合？

L2范数是指向量各元素的平方和然后求平方根。为了让L2范数的规则项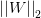最小，可以使得W的每个元素都很小，都接近于0，但与L1范数不同，它不会让它等于0，而是接近于0，这里是有很大的区别。

而越小的参数说明模型越简单，越简单的模型则越不容易产生过拟合现象。为什么越小的参数说明模型越简单？原因：限制参数很小，实际上就限制了多项式某些分量的影响很小，这样就相当于减少参数个数。

总结：

通过L2范数，可以实现了对模型空间的限制，从而在一定程度上避免了过拟合。