用R解析Mahout用户推荐协同过滤算法(UserCF)

作者：张丹，R语言中文社区专栏特邀作者，《R的极客理想》系列图书作者，民生银行大数据中心数据分析师，前况客创始人兼CTO。
个人博客 http://fens.me， Alexa全球排名70k。

前言
用R全面解析Mahout的基于用户推荐协同过滤算法(UserCF),改进的采用欧氏距离，并用R语言实现，与Mahout的结果进行对比。

Mahout是Hahoop家族用于机器学习的一个框架，包括三个主要部分，推荐，聚类，分类！
我在这里做的是推荐部分。推荐系统在现在的互联网应用中很常见，比如，亚马逊会推荐你买书，豆瓣会给你一个书评，影评。

由于时间仓促，欢迎大家一起讨论。

目录

1. Mahout的模型介绍

2. R语言模型实现

3. 算法实现的原理–矩阵变换

4. 算法总结

5. 参考资料

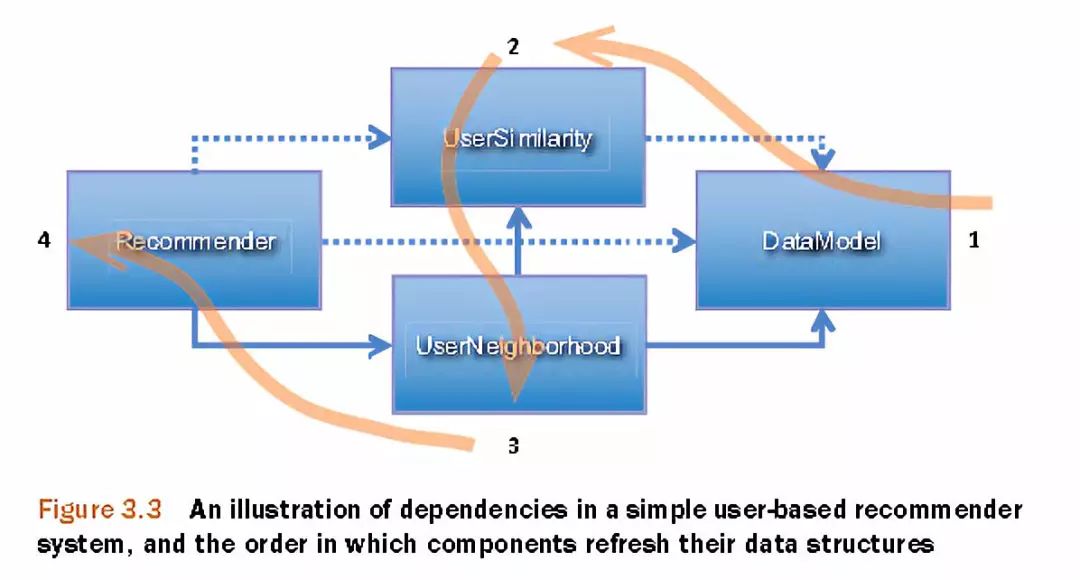
1. Mahout的模型介绍

Mahout版本

<dependency><groupId>org.apache.mahout</groupId><artifactId>mahout-core</artifactId><version>0.5</version></dependency>

Mahout程序写法

public class UserBaseCFMain {   final static int NEIGHBORHOOD_NUM = 2;   final static int RECOMMENDER_NUM = 3;   public static void main(String[] args) throws IOException, TasteException {       String file = "metadata/data/testCF.csv";       DataModel model = new FileDataModel(new File(file));       UserSimilarity user = new EuclideanDistanceSimilarity(model);       NearestNUserNeighborhood neighbor = new NearestNUserNeighborhood(NEIGHBORHOOD_NUM, user, model);       Recommender r = new GenericUserBasedRecommender(model, neighbor, user);       LongPrimitiveIterator iter = model.getUserIDs();       while (iter.hasNext()) {           long uid = iter.nextLong();           List list = r.recommend(uid, RECOMMENDER_NUM);           System.out.printf("uid:%s", uid);           for (RecommendedItem ritem : list) {               System.out.printf("(%s,%f)", ritem.getItemID(), ritem.getValue());           }           System.out.println();       }   }} 

推荐结果：

uid:1(104,4.250000)(106,4.000000)uid:2(105,3.956999)uid:3(103,3.185407)(102,2.802432)uid:4(102,3.000000)uid:5 

2. R语言模型实现

• 1). 建立数据模型

• 2). 欧氏距离相似度算法

• 3). 最紧邻算法

• 4). 推荐算法

• 5). 运行程序

由于时间仓促，R的代码中，有不少for循环影响性能，请暂时跳过!

1). 建立数据模型

FileDataModel<-function(file){data<-read.csv(file,header=FALSE)names(data)<-c("uid","iid","pref")user <- unique(data$uid)item <- unique(sort(data$iid))uidx <- match(data$uid, user)iidx <- match(data$iid, item)M <- matrix(0, length(user), length(item))i <- cbind(uidx, iidx, pref=data$pref)for(n in 1:nrow(i)){M[i[n,][1],i[n,][2]]<-i[n,][3]}dimnames(M)[[2]]<-itemM}

2). 欧氏距离相似度算法

EuclideanDistanceSimilarity<-function(M){row<-nrow(M)s<-matrix(0, row, row)for(z1 in 1:row){for(z2 in 1:row){if(z1<z2){< span="">num<-intersect(which(M[z1,]!=0),which(M[z2,]!=0)) #可计算的列sum<-0for(z3 in num){sum<-sum+(M[z1,][z3]-M[z2,][z3])^2}s[z2,z1]<-length(num)/(1+sqrt(sum))if(s[z2,z1]>1) s[z2,z1]<-1 #标准化if(s[z2,z1]< -1) s[z2,z1]<- -1 #标准化#print(paste(z1,z2));print(num);print(sum)}}}#补全三角矩阵ts<-t(s)w<-which(upper.tri(ts))s[w]<-ts[w]s}

3). 最紧邻算法

NearestNUserNeighborhood<-function(S,n){row<-nrow(S)neighbor<-matrix(0, row, n)for(z1 in 1:row){for(z2 in 1:n){m<-which.max(S[,z1])#       print(paste(z1,z2,m,'\n'))neighbor[z1,][z2]<-mS[,z1][m]=0}}neighbor}

4). 推荐算法

UserBasedRecommender<-function(uid,n,M,S,N){row<-ncol(N)col<-ncol(M)r<-matrix(0, row, col)N1<-N[uid,]for(z1 in 1:length(N1)){num<-intersect(which(M[uid,]==0),which(M[N1[z1],]!=0)) #可计算的列#     print(num)for(z2 in num){#       print(paste("for:",z1,N1[z1],z2,M[N1[z1],z2],S[uid,N1[z1]]))r[z1,z2]=M[N1[z1],z2]*S[uid,N1[z1]]}}sum<-colSums(r)s2<-matrix(0, 2, col)for(z1 in 1:length(N1)){num<-intersect(which(colSums(r)!=0),which(M[N1[z1],]!=0))for(z2 in num){s2[1,][z2]<-s2[1,][z2]+S[uid,N1[z1]]s2[2,][z2]<-s2[2,][z2]+1}}s2[,which(s2[2,]==1)]=10000s2<-s2[-2,]r2<-matrix(0, n, 2)rr<-sum/s2item <-dimnames(M)[[2]]for(z1 in 1:n){w<-which.max(rr)if(rr[w]>0.5){r2[z1,1]<-item[which.max(rr)]r2[z1,2]<-as.double(rr[w])rr[w]=0}}r2}

5). 运行程序

FILE<-"testCF.csv"NEIGHBORHOOD_NUM<-2RECOMMENDER_NUM<-3M<-FileDataModel(FILE)S<-EuclideanDistanceSimilarity(M)N<-NearestNUserNeighborhood(S,NEIGHBORHOOD_NUM)R1<-UserBasedRecommender(1,RECOMMENDER_NUM,M,S,N);R1##      [,1]  [,2]  ## [1,] "104" "4.25"## [2,] "106" "4"  ## [3,] "0"   "0"R2<-UserBasedRecommender(2,RECOMMENDER_NUM,M,S,N);R2##      [,1]  [,2]## [1,] "105" "3.95699903407931"## [2,] "0"   "0"## [3,] "0"   "0"R3<-UserBasedRecommender(3,RECOMMENDER_NUM,M,S,N);R3##      [,1]  [,2]## [1,] "103" "3.18540697329411"## [2,] "102" "2.80243217111765"## [3,] "0"   "0"R4<-UserBasedRecommender(4,RECOMMENDER_NUM,M,S,N);R4##      [,1]  [,2]## [1,] "102" "3"## [2,] "0"   "0"## [3,] "0"   "0"R5<-UserBasedRecommender(5,RECOMMENDER_NUM,M,S,N);R5##      [,1] [,2]## [1,]    0    0## [2,]    0    0## [3,]    0    0

3. 算法实现的原理–矩阵变换

所谓协同过滤算法，其实就是矩阵变换的结果!!请大家下面留意矩阵操作！
1). 原始数据

 1,101,5.0 1,102,3.0 1,103,2.5 2,101,2.0 2,102,2.5 2,103,5.0 2,104,2.0 3,101,2.5 3,104,4.0 3,105,4.5 3,107,5.0 4,101,5.0 4,103,3.0 4,104,4.5 4,106,4.0 5,101,4.0 5,102,3.0 5,103,2.0 5,104,4.0 5,105,3.5 5,106,4.0 

2). 矩阵转换

101 102 103 104 105 106 107[1,] 5.0 3.0 2.5 0.0 0.0   0   0[2,] 2.0 2.5 5.0 2.0 0.0   0   0[3,] 2.5 0.0 0.0 4.0 4.5   0   5[4,] 5.0 0.0 3.0 4.5 0.0   4   0[5,] 4.0 3.0 2.0 4.0 3.5   4   0 

3). 欧氏相似矩阵转换

 [,1]      [,2]      [,3]      [,4]      [,5][1,] 0.0000000 0.6076560 0.2857143 1.0000000 1.0000000[2,] 0.6076560 0.0000000 0.6532633 0.5568464 0.7761999[3,] 0.2857143 0.6532633 0.0000000 0.5634581 1.0000000[4,] 1.0000000 0.5568464 0.5634581 0.0000000 1.0000000[5,] 1.0000000 0.7761999 1.0000000 1.0000000 0.0000000 

4). 最近邻矩阵

top1 top2[1,]    4    5[2,]    5    3[3,]    5    2[4,]    1    5[5,]    1    3 

5). 以R1为例的推荐矩阵

 101  102  103  104  105  106  107  4    0    0    0  4.5  0.0    4    0  5    0    0    0  4.0  3.5    4    0 

6). 以R1为例的推荐结果

 推荐物品  物品得分[1,] "104"    "4.25"[2,] "106"    "4" 

4. 算法总结

我这里只是用R语言现实了Mahout的基于“用户的”，“欧氏距离”，“最近邻”的协同过滤算法。实现过程中发现，Mahout做各种算法时，都有自己的优化。

比如，算欧氏距离时，并不是标准的

similar = 1/(1+sqrt( (a-b)2 + (a-c)2 ))

而是改进的算法

similar = n/(1+sqrt( (a-b)2 + (a-c)2 )) 

1. n为b,c的个数

2. similar>1 => similar=1

3. similar<-1 => similar=-1

从而更能优化结果。

5. 参考资料：

1. Mahout In Action

2. Mahout Source Code

3. R help

推荐阅读：

用R语言把数据玩出花样

用R语言解读凯利公式

R语言高效的管道操作magrittr

R的极客理想：量化投资篇

金融投资学理论

R语言数据处理

量化投资策略

三个维度

教你如何将R语言技术应用于金融市场

↙点击“阅读原文”即可购买本书