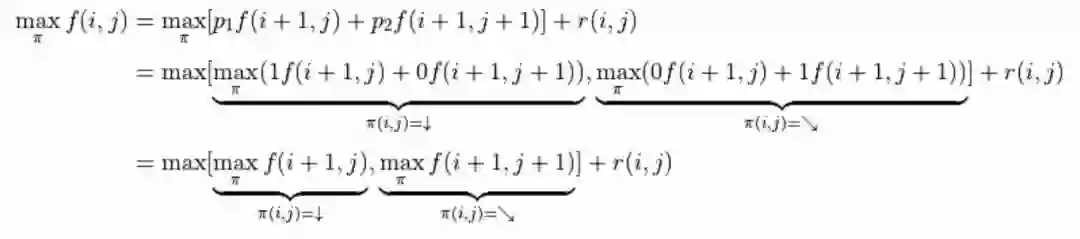简明手册 | 附录：强化学习简介（一）

2020 年 5 月 9 日 TensorFlow

文 / 李锡涵，Google Developers Expert

本文节选自《简单粗暴 TensorFlow 2》，回复 “手册” 获取合集

在上一篇文章中，我们介绍了深度强化学习(DRL)，在本章中我们将对深度强化学习一节中所涉及的强化学习算法进行入门介绍。我们所熟知的有监督学习是在带标签的已知训练数据上进行学习，得到一个从数据特征到标签的映射（预测模型），进而预测新的数据实例所具有的标签。而强化学习中则出现了两个新的概念，“智能体” 和 “环境”。在强化学习中，智能体通过与环境的交互来学习策略，从而最大化自己在环境中所获得的奖励。例如，在下棋的过程中，你（智能体）可以通过与棋盘及对手（环境）进行交互来学习下棋的策略，从而最大化自己在下棋过程中获得的奖励（赢棋的次数）。

如果说有监督学习关注的是 “预测”，是与统计理论关联密切的学习类型的话，那么强化学习关注的则是 “决策”，与计算机算法（尤其是动态规划和搜索）有着深入关联。笔者认为强化学习的原理入门相较于有监督学习而言具有更高的门槛，尤其是给习惯于确定性算法的程序员突然呈现一堆抽象概念的数值迭代关系，在大多数时候只能是囫囵吞枣。于是笔者希望通过一些较为具体的算例，以尽可能朴素的表达，为具有一定算法基础的读者说明强化学习的基本思想。

从动态规划说起

如果你曾经参加过 NOIP 或 ACM 之类的算法竞赛，或者为互联网公司的机考做过准备（如 LeetCode），想必对动态规划（Dynamic Programming，简称 DP）不会太陌生。动态规划的基本思想是将待求解的问题分解成若干个结构相同的子问题，并保存已解决的子问题的答案，在需要的时候直接利用 [1] 。使用动态规划求解的问题需要满足两个性质：

最优子结构：一个最优策略的子策略也是最优的。
无后效性：过去的步骤只能通过当前的状态影响未来的发展，当前状态是历史的总结。

我们回顾动态规划的经典入门题目 “数字三角形 (https://leetcode.com/problems/triangle/)” ：

数字三角形问题
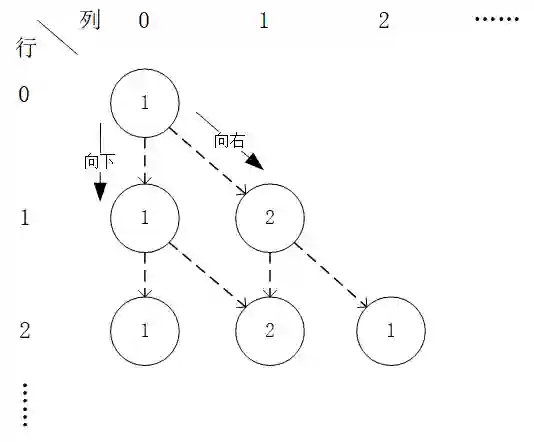
给定一个形如下图的层数字三角形及三角形每个坐标下的数字，智能体在三角形的顶端，每次可以选择向下（）或者向右（）到达三角形的下一层，请输出一个动作序列，使得智能体经过的路径上的数字之和最大。
数字三角形示例。此示例中最优动作序列为“向右-向下”，最优路径为“(0, 0) - (1, 1)

我们先不考虑如何寻找最优动作序列的问题，而假设我们已知智能体在每个坐标(i, j)处会选择的动作（例如代表智能体在(0, 0)处会选择向右的动作），我们只是单纯计算智能体会经过的路径的数字之和。我们从下而上地考虑问题，设为智能体在坐标(i, j)处的“现在及未来将会获得的数字之和”，则可以递推地写出以下等式：

(1)

上式的另一个等价写法如下：

(2)

其中

有了上面的铺垫之后，我们要解决的问题就变为了：通过调整智能体在每个坐标(i, j)会选择的动作的组合，使得的值最大。为了解决这个问题，最粗暴的方法是遍历所有的组合，例如在示例图中，我们需要决策、、的值，一共有种组合，我们只需要将8种组合逐个代入并计算，输出最大值及其对应组合即可。

不过，这样显然效率太低了。于是我们考虑直接计算 (2) 式关于所有动作组合的最大值。在 (2) 式中，与任何动作都无关，所以我们只需考虑这个表达式的最大值。于是，我们分别计算和时该表达式关于任何动作的最大值，并取两个最大值中的较大者，如下所示：

令，上式可写为，这即是动态规划中常见的“状态转移方程”。通过状态转移方程和边界值，我们即可自下而上高效地迭代计算出。

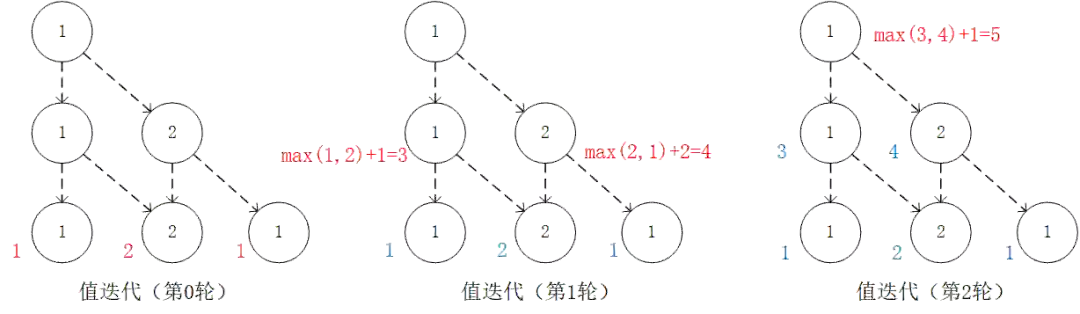
通过对 的值进行三轮迭代计算 。在每一轮迭代中，对于坐标(i, j)，分别取得当 和 时的“未来将会获得的数字之和的最大值”（即 和 ），取两者中的较大者，并加上当前坐标的数字 。

加入随机性和概率的动态规划

在实际生活中，我们做出的决策往往并非完全确定地指向某个结果，而是同时受到环境因素的影响。例如选择磨练棋艺固然能让一个人赢棋的概率变高，但也并非指向百战百胜。正所谓 “既要靠个人的奋斗，也要考虑到历史的行程”。对应于我们在前节讨论的数字三角形问题，我们考虑以下变种：

数字三角形问题（变式 1）
智能体初始在三角形的顶端，每次可以选择向下（）或者向右（）的动作。不过环境会对处于任意坐标 (i, j) 的智能体的动作产生“干扰”，导致以下的结果：

- 如果选择向下（），则该智能体最终到达正下方坐标(i+1, j)的概率为，到达右下方坐标(i+1, j+1)的概率为。

- 如果选择向右（），则该智能体最终到达正下方坐标(i+1, j)的概率为，到达右下方坐标(i+1, j+1)的概率为。

请给出智能体在每个坐标所应该选择的动作，使得智能体经过的路径上的数字之和的期望（Expectation） [2] 最大。

此时，如果你想直接写出问题的状态转移方程，恐怕就不那么容易了（动作选择和转移结果不是一一对应的！）。但如果类比前节 (2) 式描述问题的框架，我们会发现问题容易了一些。在这个问题中，我们沿用符号来表示智能体在坐标(i, j)处的“现在及未来将会获得的数字之和的期望”，则有“当前(i, j)坐标的期望 = ‘选择动作后可获得的数字之和’的期望 + 当前坐标的数字”，如下式：

(3)

其中

类比前节的推导过程，令，我们可以得到：

(4)

然后我们即可使用这一递推式由下到上计算。

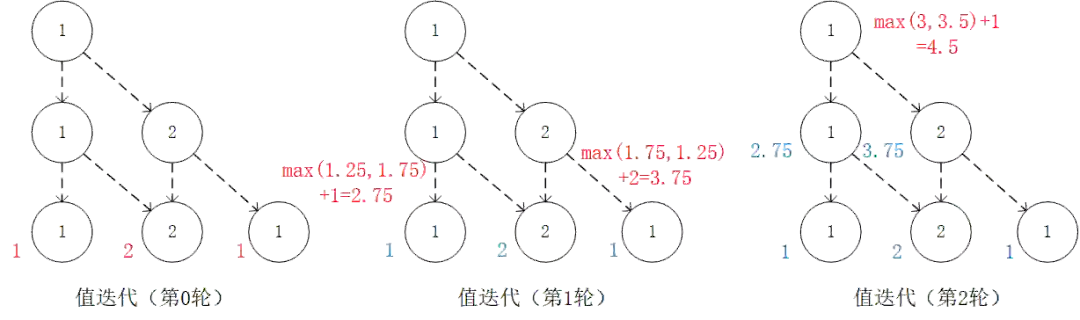
通过对 的值进行三轮迭代计算 。在每一轮迭代中，对于坐标(i, j)，分别计算当 和 时的“未来将会获得的数字之和的期望的最大值”（即 和 ），取两者中的较大者，并加上当前坐标的数字 。

我们也可以从智能体在每个坐标 (i, j) 所做的动作出发来观察 (4) 式。在每一轮迭代中，先分别计算两种动作带来的未来收益期望（策略评估），然后取收益较大的动作作为的取值（策略改进），最后根据动作更新。

策略评估-策略改进框架：通过对的值进行迭代来计算。在每一轮迭代中，对于坐标(i, j)，分别计算当和时的“未来将会获得的数字之和的期望”（策略评估），取较大者对应的动作作为的取值（策略改进）。然后根据本轮迭代确定的的值更新。

我们可以将算法流程概括如下：

初始化环境
for i = N-1 downto 0 do

（策略评估）计算第i层中每个坐标 (i, j) 选择和的未来期望和
（策略改进）对第i层中每个坐标 (i, j)，取未来期望较大的动作作为的取值
（值更新）根据本轮迭代确定的的值更新

环境信息无法直接获得的情况

让我们更现实一点：在很多现实情况中，我们甚至连环境影响所涉及的具体概率值都不知道，而只能通过在环境中不断试验去探索总结。例如，当学习了一种新的围棋定式时候，我们并无法直接获得胜率提升的概率，只有与对手使用新定式实战多盘才能知道这个定式是好是坏。对应于数字三角形问题，我们再考虑以下变式：

数字三角形问题（变式 2）
智能体初始在三角形的顶端，每次可以选择向下（）或者向右（）的动作。环境会对处于任意坐标(i, j)的智能体的动作产生“干扰”，而且这个干扰的具体概率（即上节中的和）未知。不过，允许在数字三角形的环境中进行多次试验。当智能体在坐标(i, j)时，可以向数字三角形环境发送动作指令或，数字三角形环境将返回智能体最终所在的坐标（正下方(i+1, j)或右下方(i+1, j+1)）。请设计试验方案和流程，确定智能体在每个坐标所应该选择的动作，使得智能体经过的路径上的数字之和的期望最大。

我们可以通过大量试验来估计动作为或时概率和的值，不过这在很多现实问题中是困难的。事实上，我们有另一套方法，使得我们不必显式估计环境中的概率参数，也能得到最优的动作策略。

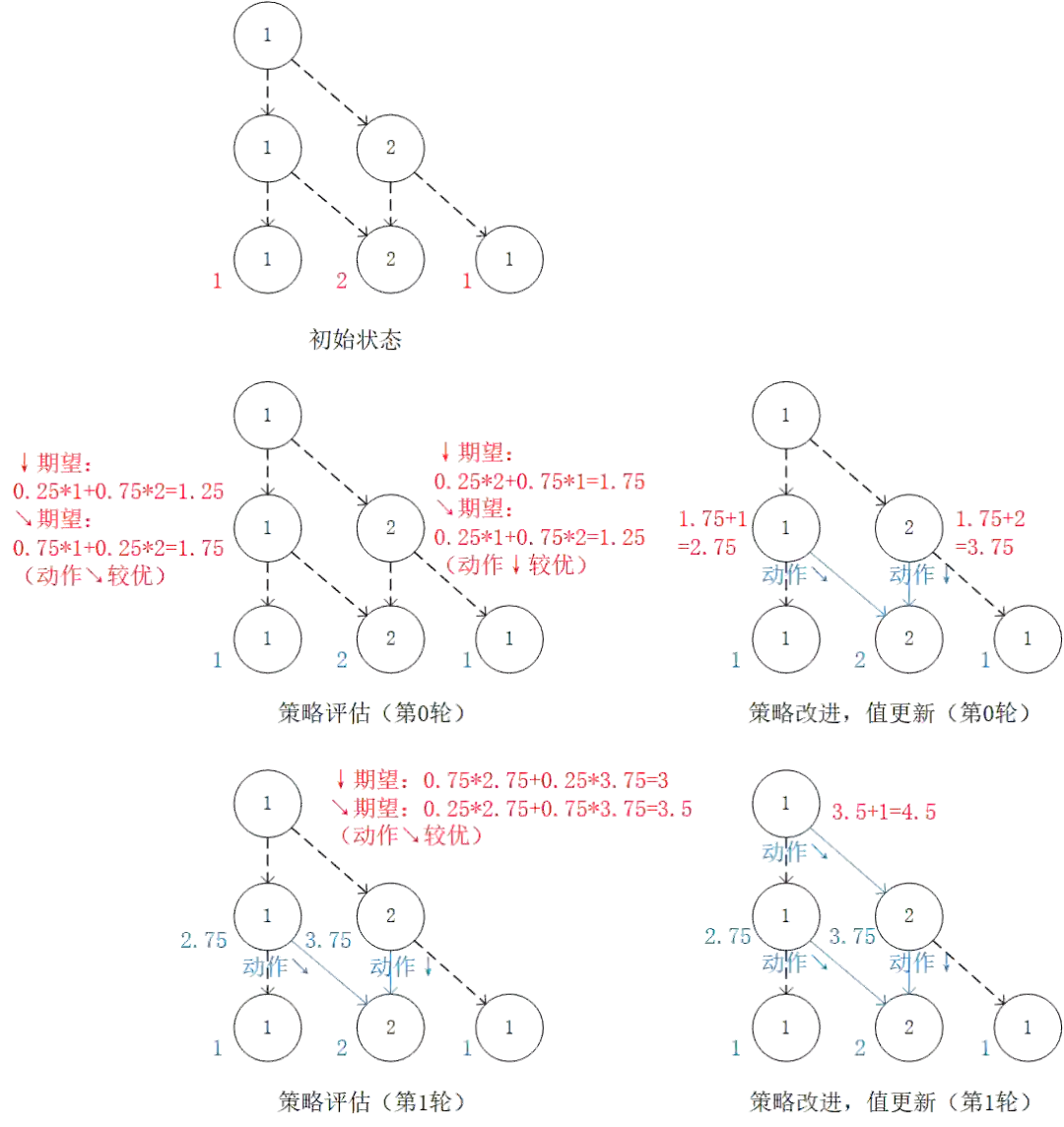
回到前节的“策略评估-策略改进”框架，我们现在遇到的最大困难是无法在“策略评估”中通过前一阶段的、和概率参数、直接计算每个动作的未来期望（因为概率参数未知）。不过，期望的妙处在于：就算我们无法直接计算期望，我们也是可以通过大量试验估计出期望的。如果我们用表示智能体在坐标 (i, j) 选择动作 a 时的未来期望 [3] ，则我们可以观察智能体在 (i, j) 处选择动作 a 后的 K 次试验结果，取这K次结果的平均值作为估计值。例如，当智能体在坐标 (0, 1) 并选择动作时，我们进行 20 次试验，发现 15 次的结果为 1，5 次的结果为 2，则我们可以估计。