BAT题库 | 机器学习面试1000题系列（第216~220题）

216.从网上下载或自己编程实现一个卷积神经网络，并在手写字符识别数据MNIST上进行试验测试。
　　解析详见：http://blog.csdn.net/snoopy_yuan/article/details/71703019

217.神经网络中激活函数的真正意义？一个激活函数需要具有哪些必要的属性？还有哪些属是好的属性但不必要的？
　　@Hengkai Guo，本题解析来源：https://www.zhihu.com/question/67366051
　　说说我对一个好的激活函数的理解吧，有些地方可能不太严谨，欢迎讨论。（部分参考了Activation function。）
　　1. 非线性：即导数不是常数。这个条件前面很多答主都提到了，是多层神经网络的基础，保证多层网络不退化成单层线性网络。这也是激活函数的意义所在。
　　2. 几乎处处可微：可微性保证了在优化中梯度的可计算性。传统的激活函数如sigmoid等满足处处可微。对于分段线性函数比如ReLU，只满足几乎处处可微（即仅在有限个点处不可微）。对于SGD算法来说，由于几乎不可能收敛到梯度接近零的位置，有限的不可微点对于优化结果不会有很大影响[1]。
　　3. 计算简单：正如题主所说，非线性函数有很多。极端的说，一个多层神经网络也可以作为一个非线性函数，类似于Network In Network[2]中把它当做卷积操作的做法。但激活函数在神经网络前向的计算次数与神经元的个数成正比，因此简单的非线性函数自然更适合用作激活函数。这也是ReLU之流比其它使用Exp等操作的激活函数更受欢迎的其中一个原因。
　　4. 非饱和性（saturation）：饱和指的是在某些区间梯度接近于零（即梯度消失），使得参数无法继续更新的问题。最经典的例子是Sigmoid，它的导数在x为比较大的正值和比较小的负值时都会接近于0。更极端的例子是阶跃函数，由于它在几乎所有位置的梯度都为0，因此处处饱和，无法作为激活函数。ReLU在x>0时导数恒为1，因此对于再大的正值也不会饱和。但同时对于x<0，其梯度恒为0，这时候它也会出现饱和的现象（在这种情况下通常称为dying ReLU）。Leaky ReLU[3]和PReLU[4]的提出正是为了解决这一问题。
　　5. 单调性（monotonic）：即导数符号不变。这个性质大部分激活函数都有，除了诸如sin、cos等。个人理解，单调性使得在激活函数处的梯度方向不会经常改变，从而让训练更容易收敛。
　　6. 输出范围有限：有限的输出范围使得网络对于一些比较大的输入也会比较稳定，这也是为什么早期的激活函数都以此类函数为主，如Sigmoid、TanH。但这导致了前面提到的梯度消失问题，而且强行让每一层的输出限制到固定范围会限制其表达能力。因此现在这类函数仅用于某些需要特定输出范围的场合，比如概率输出（此时loss函数中的log操作能够抵消其梯度消失的影响[1]）、LSTM里的gate函数。
　　7. 接近恒等变换（identity）：即约等于x。这样的好处是使得输出的幅值不会随着深度的增加而发生显著的增加，从而使网络更为稳定，同时梯度也能够更容易地回传。这个与非线性是有点矛盾的，因此激活函数基本只是部分满足这个条件，比如TanH只在原点附近有线性区（在原点为0且在原点的导数为1），而ReLU只在x>0时为线性。这个性质也让初始化参数范围的推导更为简单[5][4]。额外提一句，这种恒等变换的性质也被其他一些网络结构设计所借鉴，比如CNN中的ResNet[6]和RNN中的LSTM。
　　8. 参数少：大部分激活函数都是没有参数的。像PReLU带单个参数会略微增加网络的大小。还有一个例外是Maxout[7]，尽管本身没有参数，但在同样输出通道数下k路Maxout需要的输入通道数是其它函数的k倍，这意味着神经元数目也需要变为k倍；但如果不考虑维持输出通道数的情况下，该激活函数又能将参数个数减少为原来的k倍。
　　9. 归一化（normalization）：这个是最近才出来的概念，对应的激活函数是SELU[8]，主要思想是使样本分布自动归一化到零均值、单位方差的分布，从而稳定训练。在这之前，这种归一化的思想也被用于网络结构的设计，比如Batch Normalization[9]。

参考文献：
[1] Goodfellow I, Bengio Y, Courville A. Deep learning[M]. MIT press, 2016.
[2] Lin M, Chen Q, Yan S. Network in network[J]. arXiv preprint arXiv:1312.4400, 2013.
[3] Maas A L, Hannun A Y, Ng A Y. Rectifier nonlinearities improve neural network acoustic models[C]//Proc. ICML. 2013, 30(1).
[4] He K, Zhang X, Ren S, et al. Delving 
deep into rectifiers: Surpassing human-level performance on imagenet 
classification[C]//Proceedings of the IEEE international conference on 
computer vision. 2015: 1026-1034.
[5] Glorot X, Bengio Y. Understanding the 
difficulty of training deep feedforward neural networks[C]//Proceedings 
of the Thirteenth International Conference on Artificial Intelligence 
and Statistics. 2010: 249-256.
[6] He K, Zhang X, Ren S, et al. Deep 
residual learning for image recognition[C]//Proceedings of the IEEE 
conference on computer vision and pattern recognition. 2016: 770-778.
[7] Goodfellow I J, Warde-Farley D, Mirza M, et al. Maxout networks[J]. arXiv preprint arXiv:1302.4389, 2013.
[8] Klambauer G, Unterthiner T, Mayr A, et al. Self-Normalizing Neural Networks[J]. arXiv preprint arXiv:1706.02515, 2017.
[9] Ioffe S, Szegedy C. Batch 
normalization: Accelerating deep network training by reducing internal 
covariate shift[C]//International Conference on Machine Learning. 2015: 
448-456.

218.梯度下降法的神经网络容易收敛到局部最优，为什么应用广泛？

　　@李振华，https://www.zhihu.com/question/68109802/answer/262143638

　　深度神经网络“容易收敛到局部最优”，很可能是一种想象，实际情况是，我们可能从来没有找到过“局部最优”，更别说全局最优了。

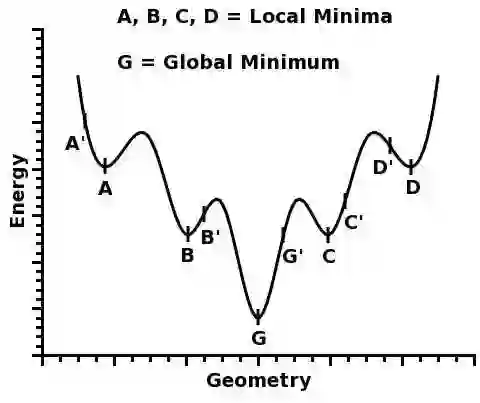
　　很多人都有一种看法，就是“局部最优是神经网络优化的主要难点”。这来源于一维优化问题的直观想象。在单变量的情形下，优化问题最直观的困难就是有很多局部极值，如

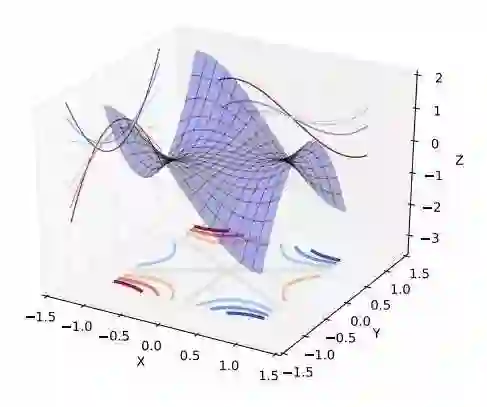
　　人们直观的想象，高维的时候这样的局部极值会更多，指数级的增加，于是优化到全局最优就更难了。然而单变量到多变量一个重要差异是，单变量的时候，Hessian矩阵只有一个特征值，于是无论这个特征值的符号正负，一个临界点都是局部极值。但是在多变量的时候，Hessian有多个不同的特征值，这时候各个特征值就可能会有更复杂的分布，如有正有负的不定型和有多个退化特征值（零特征值）的半定型

　　在后两种情况下，是很难找到局部极值的，更别说全局最优了。

　　现在看来，神经网络的训练的困难主要是鞍点的问题。在实际中，我们很可能也从来没有真的遇到过局部极值。Bengio组这篇文章Eigenvalues of the Hessian in Deep Learning（https://arxiv.org/abs/1611.07476）里面的实验研究给出以下的结论：

• Training stops at a point that has a small gradient. The norm of the gradient is not zero, therefore it does not, technically speaking, converge to a critical point.
• There are still negative eigenvalues even when they are small in magnitude.

　　另一方面，一个好消息是，即使有局部极值，具有较差的loss的局部极值的吸引域也是很小的Towards Understanding Generalization of Deep Learning: Perspective of Loss Landscapes。（https://arxiv.org/abs/1706.10239）

For the landscape of loss function for deep networks, the volume of basin of attraction of good minima dominates over that of poor minima, which guarantees optimization methods with random initialization to converge to good minima.

　　所以，很可能我们实际上是在“什么也没找到”的情况下就停止了训练，然后拿到测试集上试试，“咦，效果还不错”。

　　补充说明，这些都是实验研究结果。理论方面，各种假设下，深度神经网络的Landscape 的鞍点数目指数增加，而具有较差loss的局部极值非常少。

219.EM算法、HMM、CRF

　　这三个放在一起不是很恰当，但是有互相有关联，所以就放在这里一起说了。注意重点关注算法的思想。 
（1）EM算法 
　　EM算法是用于含有隐变量模型的极大似然估计或者极大后验估计，有两步组成：E步，求期望（expectation）；M步，求极大（maxmization）。本质上EM算法还是一个迭代算法，通过不断用上一代参数对隐变量的估计来对当前变量进行计算，直到收敛。 
　　注意：EM算法是对初值敏感的，而且EM是不断求解下界的极大化逼近求解对数似然函数的极大化的算法，也就是说EM算法不能保证找到全局最优值。对于EM的导出方法也应该掌握。 
（2）HMM算法 
　　隐马尔可夫模型是用于标注问题的生成模型。有几个参数（ π，A，B）：初始状态概率向量 π，状态转移矩阵A，观测概率矩阵B。称为马尔科夫模型的三要素。 
马尔科夫三个基本问题：

• 概率计算问题：给定模型和观测序列，计算模型下观测序列输出的概率。–》前向后向算法

• 学习问题：已知观测序列，估计模型参数，即用极大似然估计来估计参数。–》Baum-Welch(也就是EM算法)和极大似然估计。

• 预测问题：已知模型和观测序列，求解对应的状态序列。–》近似算法（贪心算法）和维比特算法（动态规划求最优路径）

（3）条件随机场CRF 
　　给定一组输入随机变量的条件下另一组输出随机变量的条件概率分布密度。条件随机场假设输出变量构成马尔科夫随机场，而我们平时看到的大多是线性链条随机场，也就是由输入对输出进行预测的判别模型。求解方法为极大似然估计或正则化的极大似然估计。 
　　之所以总把HMM和CRF进行比较，主要是因为CRF和HMM都利用了图的知识，但是CRF利用的是马尔科夫随机场（无向图），而HMM的基础是贝叶斯网络（有向图）。而且CRF也有：概率计算问题、学习问题和预测问题。大致计算方法和HMM类似，只不过不需要EM算法进行学习问题。

（4）HMM和CRF对比 
　　其根本还是在于基本的理念不同，一个是生成模型，一个是判别模型，这也就导致了求解方式的不同。 

220.CNN常用的几个模型

名称	特点
LeNet5	没啥特点-不过是第一个CNN应该要知道
AlexNet	引入了ReLU和dropout，引入数据增强、池化相互之间有覆盖，三个卷积一个最大池化+三个全连接层
VGGNet	采用1*1和3*3的卷积核以及2*2的最大池化使得层数变得更深。常用VGGNet-16和VGGNet19
Google Inception Net	这个在控制了计算量和参数量的同时，获得了比较好的分类性能，和上面相比有几个大的改进： 1、去除了最后的全连接层，而是用一个全局的平均池化来取代它； 2、引入Inception Module，这是一个4个分支结合的结构。所有的分支都用到了1*1的卷积，这是因为1*1性价比很高，可以用很少的参数达到非线性和特征变换。 3、Inception V2第二版将所有的5*5变成2个3*3，而且提出来著名的Batch Normalization； 4、Inception V3第三版就更变态了，把较大的二维卷积拆成了两个较小的一维卷积，加速运算、减少过拟合，同时还更改了Inception Module的结构。
微软ResNet残差神经网络(Residual Neural Network)	1、引入高速公路结构，可以让神经网络变得非常深 2、ResNet第二个版本将ReLU激活函数变成y=x的线性函数

 

往期题目：

BAT机器学习面试1000题系列（第1~60题）

BAT机器学习面试1000题系列（第61~100题）

BAT机器学习面试1000题系列（第101~200题）

BAT机器学习面试1000题系列（第201~205题）

BAT机器学习面试1000题系列（第206~210题）

BAT机器学习面试1000题系列（第211~215题）

---

---

课程咨询｜微信：julyedukefu

七月热线：010-82712840