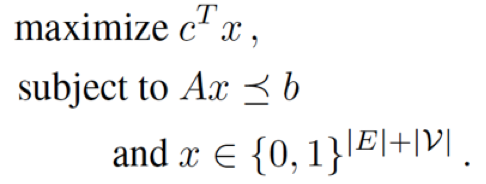【学界】 CVPR 2018最佳论文作者亲笔解读:研究视觉任务关联性的Taskonomy
作者:沈博魁
来源:机器之心
本文作者沈博魁是斯坦福本科生/准博士生,也是 CVPR 2018 最佳论文《Taskonomy:Disentangling Task Transfer Learning》的共同二作。鉴于作者在 Poster Session时发现很多人对Taskonomy的理解有偏差,沈博魁在知乎写了一篇Taskonomy的中文解读,希望能对大家有帮助。很多专业词汇的中文翻译可能有偏差,希望大家见谅。如果有问题,欢迎大家评论私信。
➤ 细节请查看知乎文章:https://zhuanlan.zhihu.com/p/38425434
➤ Taskonomy的网站:taskonomy.stanford.edu
梗概
人类的视觉具备多种多样的能力,计算机视觉界基于此定义了许多不同的视觉任务。长远来看,计算机视觉着眼于解决大多数甚至所有视觉任务,但现有方法大多尝试将视觉任务逐一击破。这种方法造成了两个问题:
第一,逐一击破需要为每一项任务收集大量数据,随着任务数量的增多,这将会是不可行的。
第二,逐一击破会带来不同任务之间的冗余计算和重复学习。
一般来说,逐一击破的策略忽略了视觉任务之间的关联性,比如法线(Surface Normals)是由深度(Depth)求导得来,语义分割(Semantic Segmentation)又似乎和遮挡边缘测试(Occlusion edge detection)有着千丝万缕的关联。基于上述两个问题,我们希望能有效测量并利用视觉任务之间的关联来避免重复学习,从而用更少的数据学习我们感兴趣的一组任务。
Taskonomy是一项量化不同视觉任务之间关联、并利用这些关联来最优化学习策略的研究。如果两个视觉任务A、B具有关联性,那么在任务A中习得的representations理应可为解决任务B提供有效的统计信息。由此我们通过迁移学习计算了26个不同视觉任务之间的一阶以及高阶关联。
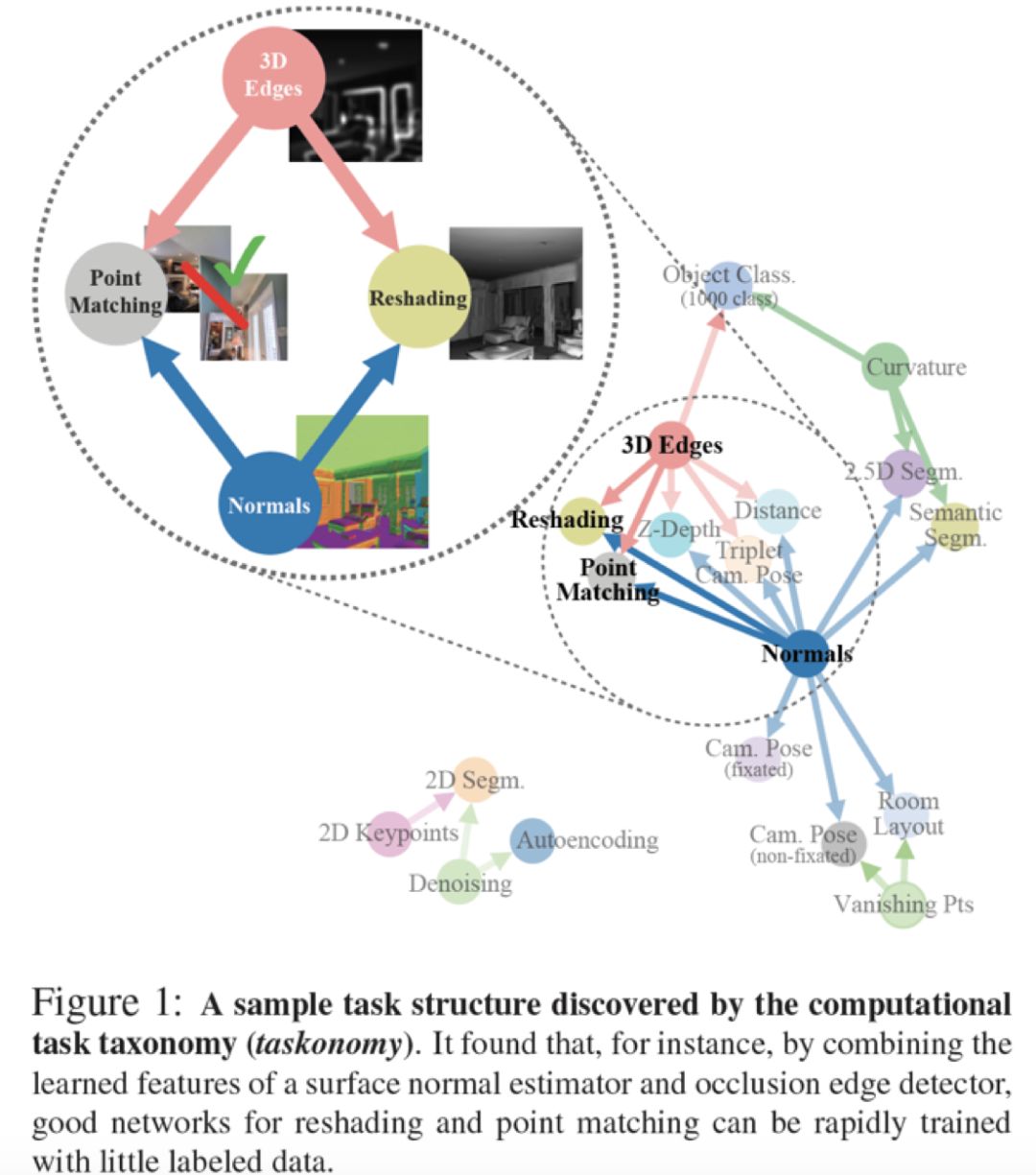
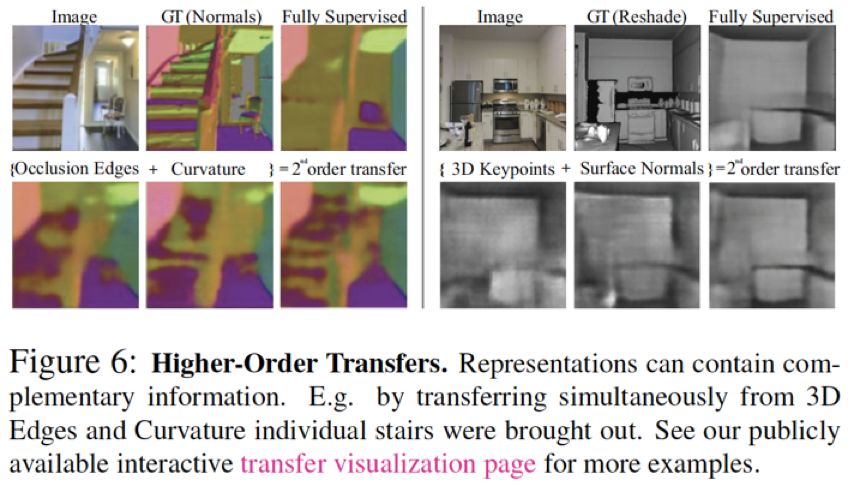
如图一,如果有预测法线的网络和预测遮挡边缘测试的网络,我们可以通过结合两个网络的representations来快速通过少量数据解决Reshading和点匹配 (Point matching)。基于这些关联,我们利用BIP (Binary Integer Programming) 求得对于一组我们感兴趣的任务,如何去最优分配训练数据量。比如,如果想最高效地解决10个问题,利用Taskonomy提供的学习策略可以减少2/3的训练数据量。
方法
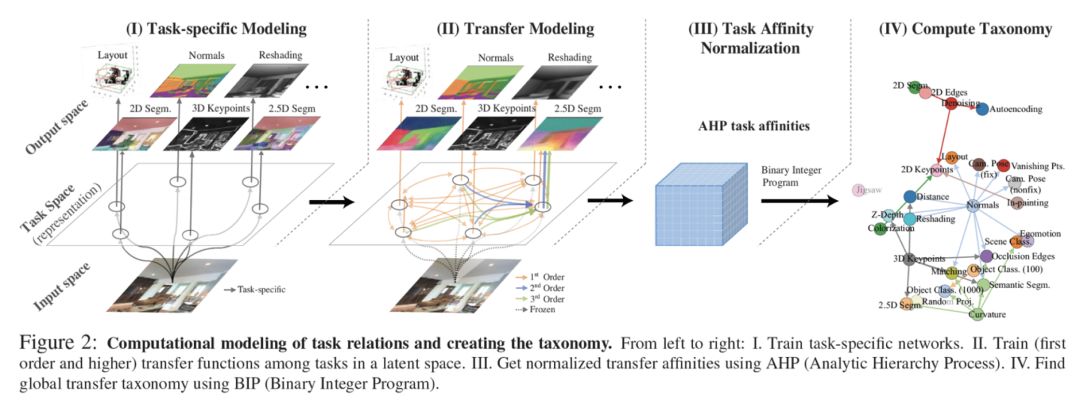
简单概括,方法分为两个大阶段,四个小步。
第一大阶段涉及前三小步,我们要量化不同视觉任务之间的关联,并将任务关联表达成一个affinity matrix(关联矩阵)。
第二大阶段,也就是最后一小步,我们对求得的affinity matrix进行最优化,求得如何最高效地去学习一组任务。这个最高效的策略会由一个指向图 (directed graph) 来表示,我们称此指向图为Taskonomy。词语上Taskonomy是Task (任务) 和 Taxonomy (分类论) 的合并简称。
>>>> 问题定义
首先,我们来定义我们想要解决的问题。我们想在有限的监督预算γ下最大化我们在一组目标任务(target tasks) T = {t1,...,tn}上的表现。同时,我们有一组起始任务 (source tasks) S,其定义为我们可从零学习的任务。监督预算γ的定义为多少起始任务我们愿意从零开始学习(从零开始学习需要收集大量数据,监督预算表达了我们所面对的金钱、计算力和时间上的限制)。其中,
T \ S 代表了我们感兴趣但不能从零学习的任务,比如一个只能有少量数据的任务。
S \ T 代表了我们不感兴趣但可以从零学习(来帮助我们更好的学习𝓣)的任务,如jigsaw、colorization等自我监督的视觉任务。
T ∩ S 代表了我们既感兴趣又能从零学习的任务,但因为从零学习会消耗监督预算,我们希望从中选择出符合预算的一组从零学习,余下的通过少量数据的迁移学习来实现。
我们称 V = T ∪ S 为我们的任务词典 (task dictionary)。最后,我们对视觉任务t的定义为一个基于图片的方程 f(t)。
如下图所示,我们收集了一个有四百万张图片的数据题,每张图片均有26个不同视觉任务的标注 (ground truth)。这26个任务涵盖了2D的、3D的和语义的任务,构成了本项research的任务词典。因为这26个任务均有标答,S也为这26个任务。
下面,我们进入第一大阶段,量化视觉任务的关联。
>>>> 第一步:从零学习
对于每个起始任务,我们为其从零开始学习一个神经网络。为了能更好地控制变量从而比较任务关联,每个任务的神经网络具有相似的encoder-decoder结构。所有的encoder都是相同的类ResNet50结构。因为每个任务的output维度各不相同,decoder的结构对不同的任务各不相同,但都只有几层,远小于encoder的大小。
(注:CVPR poster session期间有人问起,decoder泛指readout functions,比如classification的FC Layers也算为decoder)
>>>> 第二步:迁移学习
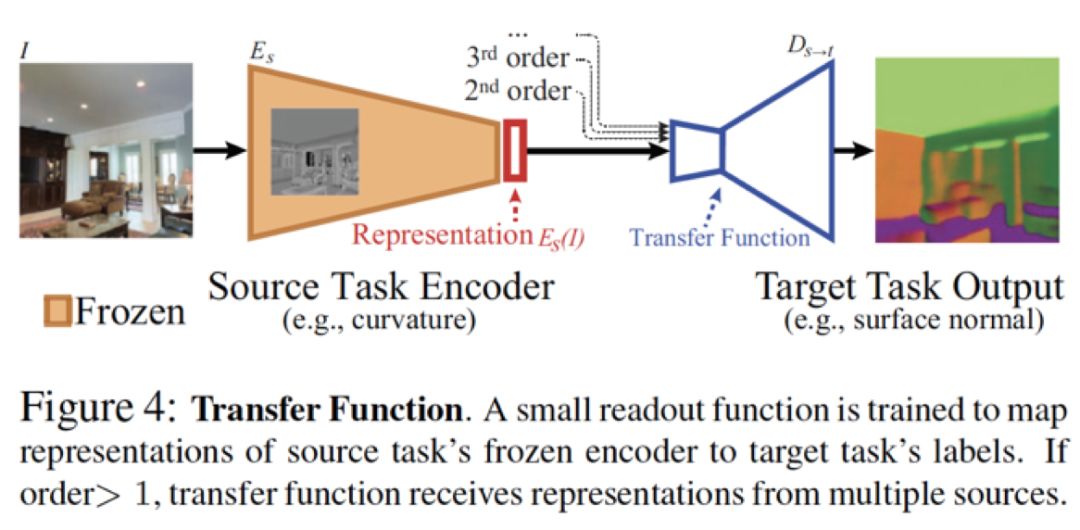
如上图所示,对于每一对起始任务 s ∈ S 和目标任务 t ∈ T,我们将以s的representation作为输入来学习t。我们将冻结任务s的encoder 参数,并基于encoder的输出 (representations) 学习一个浅层神经网络read out function。
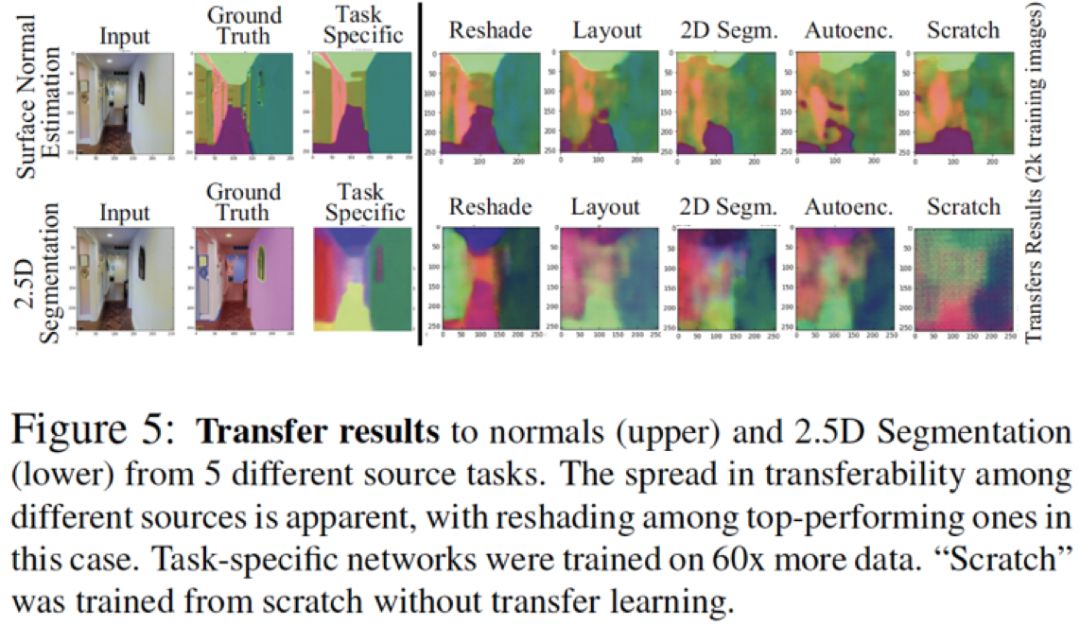
如下图所示,对于t,不同的起始任务的representation会对迁移表现造成不同的影响。更具关联的s会为t提供更有效的统计信息,从而仅用1/60的训练数据(相较于从零学习)就能取得不错的结果;相反不具备关联的s则并不能有此表现。因此,我们认为基于s的representation的迁移学习在t任务中的表现可以很好地代表了s之于t的关联性。
上述迁移代表了任务之间一对一的关联,我们称其为一阶关联。如下图,几个任务之间可能具有互补性,结合几个起始任务的representations会对解决目标任务起到帮助。因此,我们也研究了任务之间多对一的关联,我们称其问高阶关联。在这种情况下,我们concatenate几个起始任务的representation当作目标任务的输入,其余细节跟上段类似。
因为高阶的任务组合数量太大,我们基于一阶表现选择了一部分的组合进行迁移学习。对于小于五阶的高阶,我们根据一阶的表现,将前五的所有组合作为输入。对于n > 5阶,我们选择结合一阶表现前n的起始任务作为输入。
>>>> 第三步:Ordinal Normalization
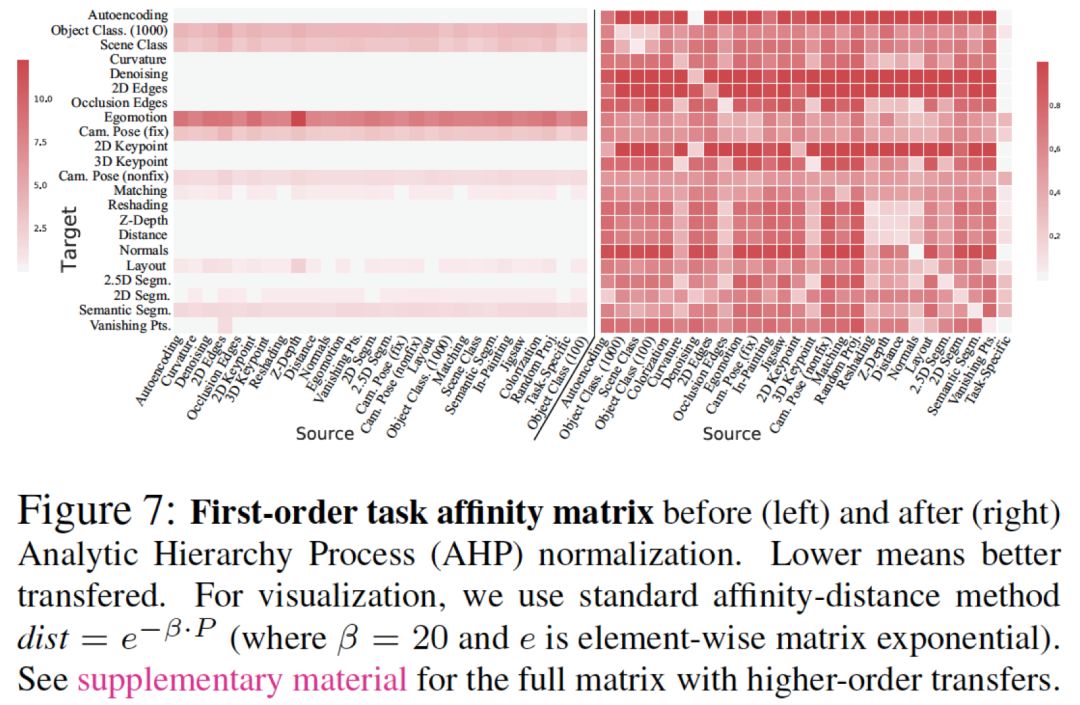
这一步的目标为用一个affinity matrix量化任务之间的关联。虽然从上步习得的迁移网络中我们获得了许多的loss值 ,但因这些loss值来自于不同的loss 函数,它们的值域有很大差别。
如果我们把这些loss值直接放入一个矩阵(上图左,纵轴为目标任务、横轴为起始任务),那么这个矩阵内的值及其不均匀,并不能有效反应任务之间的关联。同时,简单的线性规范化也并不能解决问题,因为任务的loss值和表现并不构成线性关系(0.01的l2 loss并不代表其表现两倍好于0.02)。
由此,我们采用Ordinal Normalization(基于序数的规范化)来将loss值转换为关联度。该方法基于运筹学中的AHP (Analytic Hierarchy Process)。具体细节见论文或知乎,概括来讲,affinity matrix中的第 (i, j) 个值为利用第 i 个起始任务迁移后,其网络有多大的几率表现好于用第 j 个网络(我们在下文称其为 i 对于 j 的胜率)。
至此第一大阶段完结,我们通过上述affinity matrix量化了任务之间的关联性。
>>>> 第四步:BIP最优化
最后一步,我们要基于affinity matrix求得如何最有效地学习一组我们感兴趣的任务。我们可以这个问题想象成一个subgraph selection的问题:选择一些任务从零学习,剩下的任务用少量数据进行迁移学习,具体迁移学习的策略由subgraph中的edge来决定(对一条directed edge,起始点代表我们从零学习的一个任务,终点代表要进行迁移的目标任务)。基于此,我们可以通过解如下最优化问题来得到最优解:
这个最优问题有三个限制条件。
1. 如果我们选择了一个迁移,那么迁移的起始任务(可能为高阶起始集)和目标任务均要出现在subgraph中
2. 每个目标任务有且仅有一个迁移(我们将从零学习在途中定义为从自己到自己的迁移,即一条自己到自己的edge)
3. 不超过监督预算
这三个限制条件的具体数学表达如下:
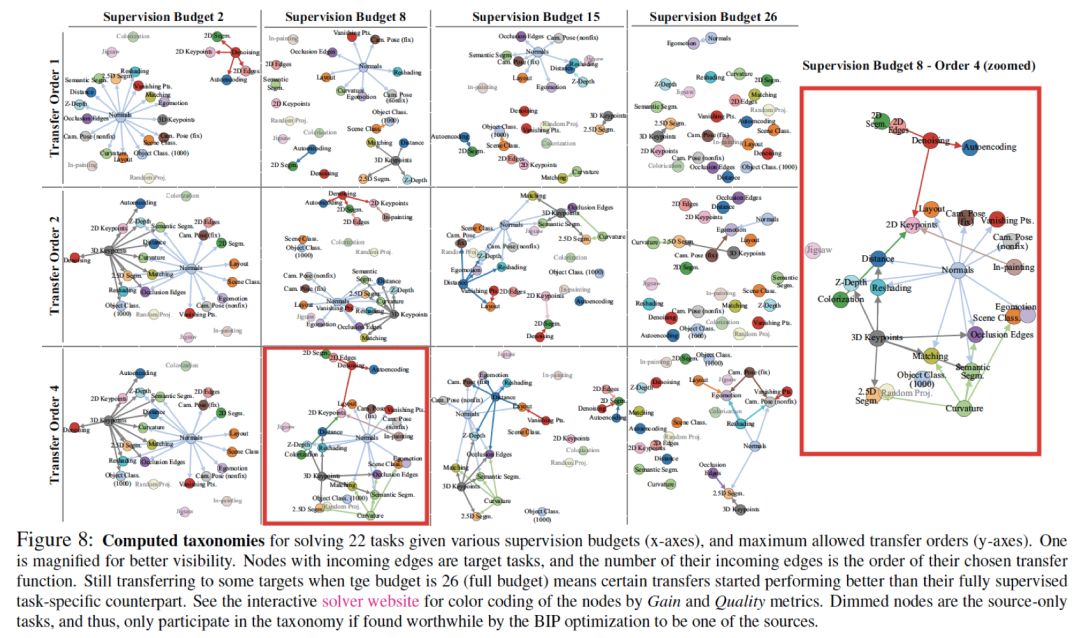
至此,我们通过解最优subgraph selection从而获得了最有效迁移学习策略,如下图:
实验结果
Taskonomy项目训练了3000+个神经网络,总耗时~50000小时的GPU。从零学习消耗120k张图片,迁移学习为16k张图片。
我认为现有公众号对Taskonomy翻译中最不准确的是对Taskonomy实验部分的评论。如文章一开头所说,Taskonomy的目标为用有限的监督预算来最有效地解决一组任务,并不是将state of the art提高百分之几。本文想宣扬的中心思想是计算机视觉界应注重视觉任务间的关联性,并让这些关联性为我们所用。回到本文的具体用途,Taskonomy的用途有两个:
1. Taskonomy作为解决一组任务的方法。
2. 用Taskonomy的任务词典解决一个只有少量数据的新任务。
以下试验结果分为两个部分,分别对应以上两点。
>>>> 一:解决一组任务
如何衡量Taskonomy解决一组任务的有效性?我们设定了两个评判标准。
1. 迁移获利 (Gain) : 如果我们不进行迁移学习,我们只能基于少量的数据从零学习。迁移获利是指迁移学习相较于从零学习的胜率(见Ordinal Normalization部分)。
2. 迁移质量 (Quality) : 用少量数据迁移学习相较于用大量数据从零学习的胜率。
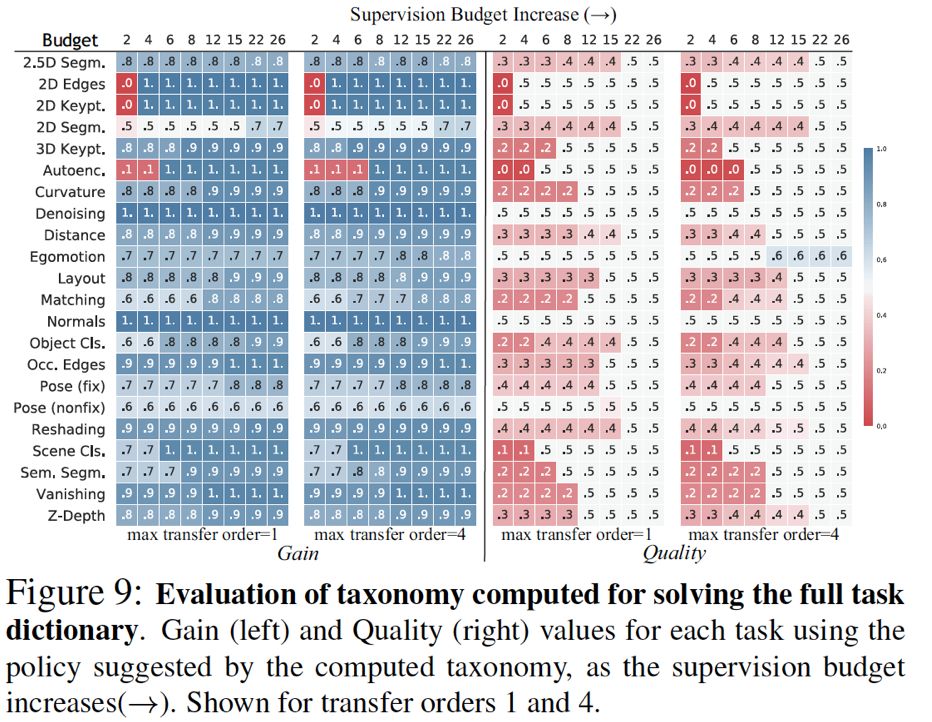
下图是Taskonomy的迁移获利 (左) 和质量 (右) 的图表。两图的纵轴为所有目标任务,横轴为监督预算,胜率在0-1之间。可见,对于一个26个任务的目标集,在只有一半甚至1/3的监督预算时,Taskonomy计算出的监督分配会使整体表现远远打败从零学习(迁移获利),并近似于(胜率超过40%)大量数据完全监督学习(迁移质量)。
>>>> 二:解决新任务
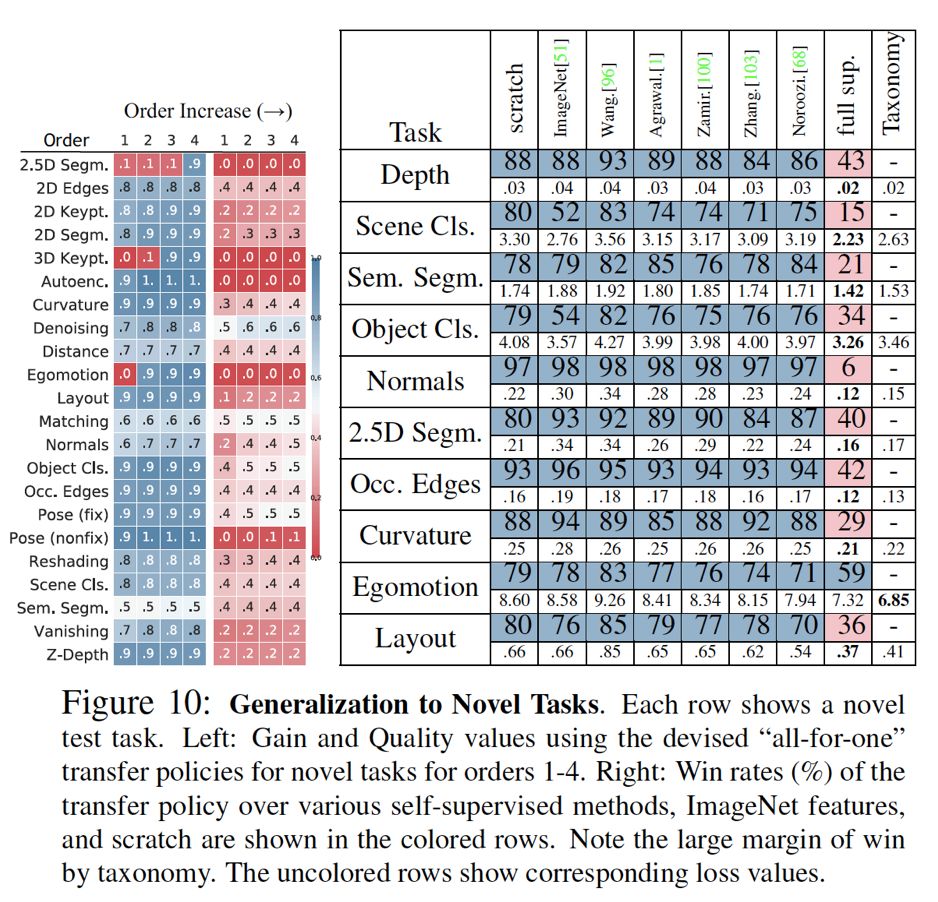
对于解决新任务,我们可以把我们任务词典里的目标任务当作一个新任务,模拟只有少量数据的情况。实验结果如下,我们可以发现Taskonomy的表现超过了现有的行业pretrained features(包括imagenet fc7)。
总结
在Taskonomy项目里,我们的目标是着眼于一组任务,并利用任务之间的关联性减少总体数据使用量。为此,我们量化了视觉任务的关联性,并基于求得的affinity matrix最优化得到如何分配任务监督数据量。实验表明,视觉任务之间确实存在很强的关联性,我们能通过更少的数据很好地解决一组任务。
☞【学界】OpenPV:中科院研究人员建立开源的平行视觉研究平台
☞【学界】ParallelEye:面向交通视觉研究构建的大规模虚拟图像集
☞【CFP】Virtual Images for Visual Artificial Intelligence
☞【最详尽的GAN介绍】王飞跃等:生成式对抗网络 GAN 的研究进展与展望
☞【智能自动化学科前沿讲习班第1期】王飞跃教授:生成式对抗网络GAN的研究进展与展望
☞【智能自动化学科前沿讲习班第1期】王坤峰副研究员:GAN与平行视觉
☞【重磅】平行将成为一种常态:从SimGAN获得CVPR 2017最佳论文奖说起
☞【前沿】谷歌提出Sim2Real:让机器人像人类一样观察世界
☞【深度】何恺明CVPR演讲:深入理解ResNet和视觉识别的表示学习(41 PPT)
☞【深度】小数据,大任务!详解英特尔中国研究院的视频物体分割解决方案
☞【学界】Ian Goodfellow等人提出对抗重编程,让神经网络执行其他任务