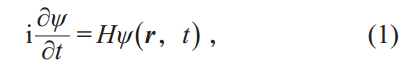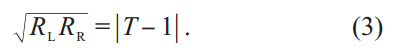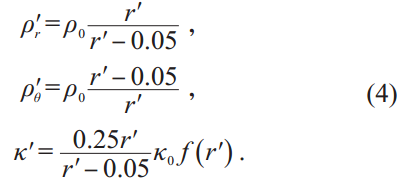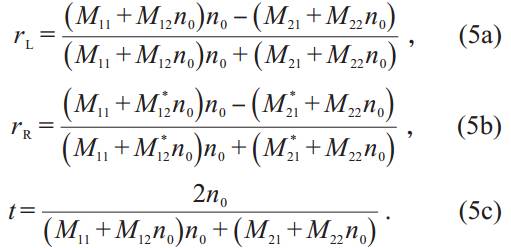宇称时间对称性声学

2017 年 11 月 29 日 中国物理学会期刊网 祝雪丰等

作者：祝雪丰彭玉桂沈亚西 (华中科技大学物理学院)

1 宇称时间对称性破缺

自然界中各种各样的物理现象都存在一些内在的不变性或对称性。例如，物理过程在空间反演和时间反演下能够回到初始状态，对应于物理学中两个基本对称性：宇称和时间对称。对于人眼看不见的微观过程，宇称和时间对称依然扮演着十分重要的角色，确保了物理可观测量为实数和几率守恒。具体而言，微观过程中波函数分布为ψ(r，t)的粒子时空演化规律可由薛定谔方程来描述：

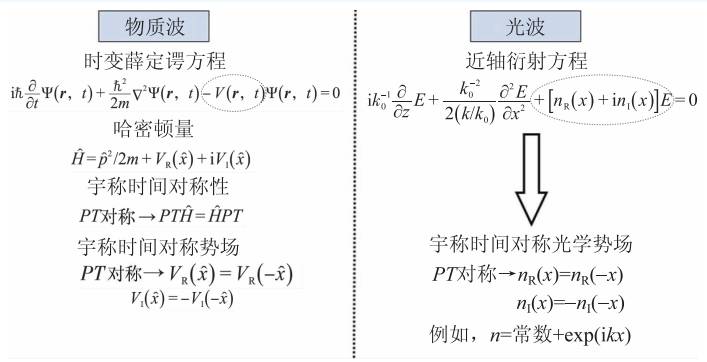
其中ψ为粒子波函数时空分布，H为哈密顿算符，r为粒子空间位置坐标矢量，t为时间，i为虚数单位。宇称作用算符P 和时间作用算符T 分别定义为Pψ( r，t) = ψ(-r，t) 和Tψ(r，t) =ψ*(r， - t) 。若H=PTHPT，我们称该哈密顿算符为宇称时间对称算符。经典量子力学中，哈密顿算符一般要求为厄米算符，其满足宇称时间对称性且本征值为实数(可观测量)。1998年，Bender 和Boettcher 研究了非厄米哈密顿算符宇称时间对称性和本征谱之间的关系，指出非厄米—算符本征值在宇称时间对称性下亦可为实数，并进一步发现非厄米—哈密顿算符宇称时间对称性破缺会导致本征值由实数变为复数。而后，宇称时间对称量子体系相关研究如火如荼地开展。然而由于满足宇称时间对称性的势场在现实中难以构建，相关实验证实仍然缺乏，因此关于宇称时间对称在量子体系中的重要性仍在争论之中。近些年来，研究人员发现通过时变薛定谔方程和近轴衍射方程形式相似性可在经典波体系中构建满足宇称时间对称性的系统，如图1 所示。对于宇称时间对称经典波系统，其材料折射率满足实部对称分布n_R(x) = n_R(-x) 和虚部反对称分布n_I(x) = -n_I(-x) ，例如， n = exp(ikx) ，i 为虚数单位。那为什么研究人员对经典波体系中宇称时间对称性很感兴趣呢？主要原因有三：第一，由于经典波体系实验技术较为成熟，我们可以在经典波体系中构建宇称时间对称系统，从而具体研究其相关性质；第二，宇称时间对称系统是开放系统，其散射矩阵本征值一般为复数且存在多重简并点。简并点在物理上对应于奇点。在简并点附近，系统会呈现出一些有趣的特性，例如，非零几何相位、单向衍射、激射和完美吸收共存体等。另外，满足宇称时间对称性的开放系统会展现出封闭系统的一些性质；第三，在很多物理过程中，损耗一般被视为是一种有害因素，应当尽量抑制，而宇称时间对称系统却将损耗利用起来实现一些有用的功能，这在物理和应用上非常具有启发性。

图1 时变薛定谔方程和近轴衍射方程

2 宇称时间对称性声学

鉴于时变薛定谔方程和近轴衍射方程形式相似性，我们很自然地会考虑在声学领域构建宇称时间对称系统。我们发现当材料弹性模量满足κ(r) = κ*(-r) 和密度满足ρ(r) = ρ(-r) 时，整个系统满足宇称时间对称性。为了更为直观地阐述声学宇称时间对称系统的相关性质，我们设计了一个简单的一维声学宇称时间对称系统，如图2所示。然而，我们发现材料弹性模量须为一个复数，且虚部空间分布有正有负。一般而言，自然界中声学材料弹性模量虚部为正，表明材料存在由弹性粘滞导致的声损耗。若弹性模量虚部为负，则意味着该材料是一种声学增益媒质，目前人们还未发现天然的声学增益媒质。对于简单的一维双端口系统，我们可通过设计精巧的电路反馈系统，结合麦克风和扬声器等辅助设备，构建出一种等效的声学增益系统(其散射矩阵与特定长度声学增益媒质完全相同)。图2 中，一维声学宇称时间对称系统由3 个损耗(增益)区域和5 个无损区域构成。其中，损耗(增益)媒质的材料参数为： κ_l(g) = 1.75 × 10⁵ ± 1.72 × 10⁴i Pa (i 为虚数单位)和ρ_l(g) = 1.49 kg/m³ ，无损媒质的材料参数为：κ_p= 1.42 × 10⁵Pa 和ρ_p = 1.2 kg/m³ 。

对于满足宇称时间对称性的一维双端口系统(图2)，其左右反射系数r_L(R)和透射系数t 满足下式：

进一步我们可以推导出左右反射率R_L(R) ≡ |r_L(R)|²和透射率T ≡ |t|² 满足下式：

公式(3)是无损封闭系统中能量守恒公式的一种推广。当T<1 且R_L=R_R=R 时，我们可以得到更为熟悉的能量守恒关系式T+R=1。在一维宇称时间对称系统中，由于材料参数虚部的不对称性，左反射率R_L与右反射率R_R一般不相同。一个很有趣的效应会发生在完全透射情况。根据公式(3)，当T=1，我们可以得到左右反射率乘积为0，即R_LR_R=0。这时，宇称时间对称系统可能处于三种状态。状态一，系统的左右反射率一个为零，一个为非零有限值，例如R_L=0 和R_R≠0；状态二，系统的左右反射率一个为零，一个为无限大，例如R_L=0 和R_R=∞ ；状态三，系统的左右反射率均为零，即R_L=R_R=0。

图2 一维声学宇称时间对称系统示意图。该系统在散射矩阵本征谱简并点处呈现单向透明。L区域填充损耗媒质，其长度为0.148 m。G区域填充增益媒质，其长度为0.148 m。其余区域填充无损媒质，其长度为0.015 m

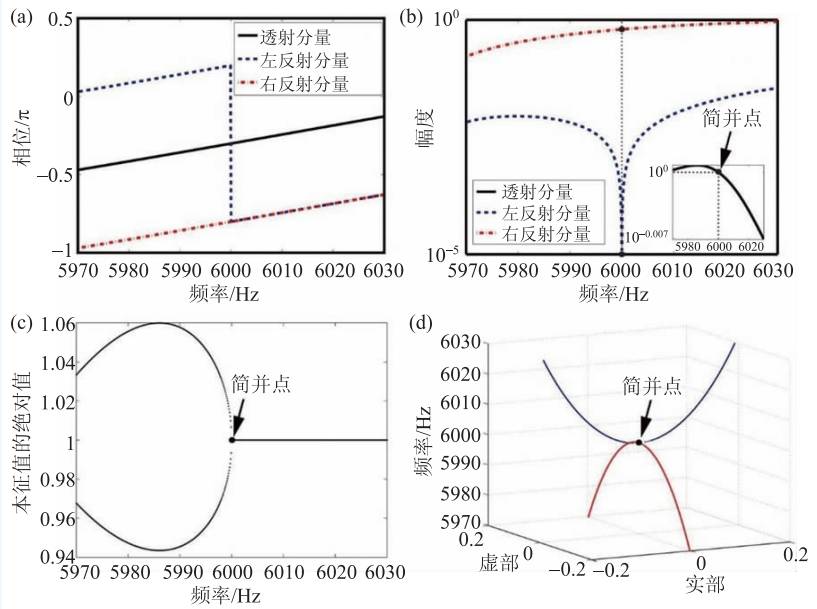
基于声学传递矩阵法，我们可以计算出图(2)所示一维宇称时间对称系统的声散射矩阵S = {t，r_R；r_L，t} ，从而得到系统的散射特性(图3)。根据图3(a)和(b)的结果，我们得到当透射率小于1 时(频率大于6000 Hz)，左右反射系数位相相等；当透射率大于1 时( 频率小于6000 Hz)，左右反射系数位相相差π。另外，系统透射系数位相与左右反射系数位相相差±π/2。当透射率等于1 时(频率等于6000 Hz)，我们发现左反射系数位相发生π 跃变，此时左反射率严格为0 (R_L=0)；右反射系数位相连续变化，此时右反射率不为零(R_R≈0.39)。这里需要说明的是，系统全透射情况下，单向反射效应并不对应于系统单向隐形，这是因为声波经过宇称时间对称系统和相同长度均匀背景媒质所产生的相位延迟并不相同。因此，对于左入射情况，即使透射率为1，反射率为0，我们依然可以通过测量相位信息来判断该宇称时间对称系统是否在声传播路径上。

图3 (a)一维宇称时间对称系统中左右反射和透射分量的相位；(b)一维宇称时间对称系统中左右反射和透射分量的幅度；(c)一维宇称时间对称系统散射矩阵本征值的绝对值谱图；(d)一维宇称时间对称系统散射矩阵本征向量第二个分量的实部和虚部频谱图(第一个分量归一化)

一维宇称时间对称声学系统中，透射率从小于1 变为大于1 可与宇称时间对称性破缺相关联。对于双端口声学系统，散射矩阵的本征值可表示为λ_1，2 = t ±√r_Lr_R ，本征向量转置可表示为(1± √(r_L/r_R ))。利用公式(2)，散射矩阵的本征值可进一步写成λ_1，2 = t(1 ± i √((1 - T )/T) )，i 为虚数单位。本征值绝对值谱图如图3(c)所示。当透射率小于1时(频率大于6000 Hz)，两个本征值共轭且绝对值为1( | λ₁| = | λ₂|= 1 )，这时系统处于宇称时间对称状态；当透射率大于1时(频率小于6000 Hz)，两个本征值绝对值一个大于1，一个小于1( | λ₁| ≠ | λ₂|)，这时系统处于宇称时间对称破缺状态。我们可以进一步考察本征向量第二个分量±√ (r_L /r_R) 的谱图，如图3(d)所示。蓝色曲线对应于宇称时间对称状态，此时本征向量分量均为实数；红色曲线对应于宇称时间对称破缺状态，此时本征向量分量均为虚数。值得一提的是，这些宇称时间对称系统的相关性质在光学和电子学等领域被理论和实验所证实。

3 非盲声学隐身衣

鉴于声波方程在坐标变换下形式保持不变，我们可以将宇称时间对称声学和变换声学结合起来，从而设计各种单向响应声学器件。这一节中，我们介绍一种单向隐形声学斗篷。我们首先在虚空间(r，θ) 构建一种特殊的宇称时间对称声学媒质，其材料参数复调制满足δe^{iβ ⋅ r} ，如图4(a)和(b)所示。其中， δ 和2π/| β | 分别为复调制的强度和周期。图4(a)和(b)中，宇称时间对称声学媒质材料密度和模量为： ρ₀ = 1.2 kg/m³和κ₀ =1.42 × 10⁵{1 + 0.1 exp[i 219.7r cos(θ)]} Pa(r < 0.1 m)，i 为虚数单位。空气的密度和模量分别为：ρ₀ = 1.2 kg/m³ 和κ₀= 1.42 × 10⁵ Pa 。然后，我们建立一个虚空间(r，θ) 和实空间(r′，θ′) 的映射关系式： r = f (r′) 和θ = θ′ ，其中f (r′) =0.1(r′- 0.05)/(0.1 - 0.05) (0.05 < r′< 0.1 m) 。根据变换声学理论，我们可以得到在实空间中宇称时间对称声学隐身衣的材料参数分布：

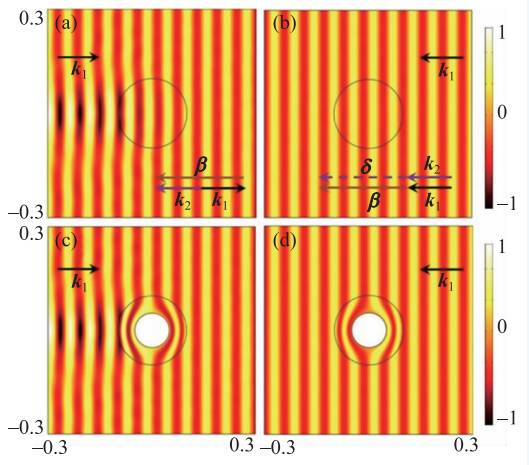
事实上，材料参数复调制δe^{iβ ⋅ r} 可以等效为一个复声栅，其可提供一个单向波矢β。波矢为k₁ 的入射平面波与复声栅相互作用，可产生一个波矢为k₁+ β 的衍射模式。入射平面波与衍射模式之间的模式跃迁只有当位相匹配大致满足时才会发生，即δ = k₁ + β - k₂ ≈ 0 ，其中k₂ 是衍射模式的波矢且|k₁| = |k₂| 。如果入射平面波与衍射模式之间位相失配δ ≠ 0 ，模式跃迁则被有效抑制。宇称时间对称声学隐身衣的工作原理如图4 所示。当平面波从左侧入射时，由于位相匹配大致满足k₂ ≈ k₁ + β (如图4(a)中波矢关系所示)，我们可以观察到明显的布拉格反射分量，从而能够感知被隐身物体的存在。当平面波从右侧入射时，由于位相失配， k₂ ≪ k₁ + β (如图4(b)中波矢关系所示)，散射分量为倏失波，物体被完美隐身。图4(c)和(d)展示了实空间宇称时间对称声学隐身衣的单向隐身效果。这里需要说明的是，在图4(c)中，位于宇称时间对称声学隐身衣右侧的观测者依然看不见被隐形的物体，这是因为满足位相匹配的衍射分量为反向传输，无法传至右侧的观测者。事实上，我们可以通过设计让满足位相匹配的衍射分量前向传输。然而，由于Lorenz(洛伦兹)互易的约束，满足位相匹配衍射分量的传输方向不能为正前方，即不能和入射波传播方向一致。

图4 (a)和(b)分别为虚空间中声波左右入射单向隐形声学斗篷对应的声压场图；(c)和(d)分别为实空间中声波左右入射单向隐形声学斗篷对应的声压场图。当平面波从左侧入射时，由于波矢 k匹配，我们可观测到一个强反射分量，从而能够感知隐形斗篷的存在。当平面波从右侧入射时，由于波矢 k失配，系统无反射分量从而完美隐形。入射声波波长为0.0572 m，坐标单位为m

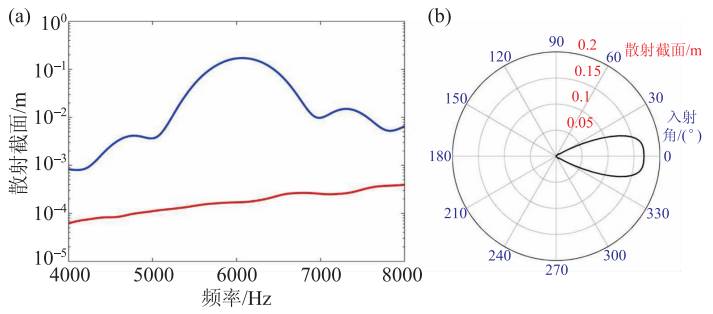
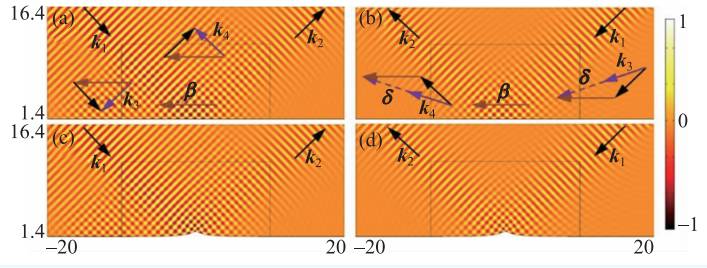
宇称时间对称声学斗篷单向隐身并非一个窄带效应。图5(a)表明在入射声波频率为5 kHz 到8 kHz 范围内都能观测到单向隐身效应。然而需要说明的是，宇称时间对称声学斗篷的单向隐身频段也极大地受限于超常材料自身的强色散性质。图5(b)表明在入射角偏离水平线正负30 度范围内都能观测到单向隐身效应。我们也可以基于相同的原理设计一个单向隐形地毯斗篷。虚空间中，如图6(a)和(b)所示，媒质材料密度和模量分别为： ρ₀ = 1.2 kg/m³ 和κ₀= 1.42 × 10⁵ ×{1 + 0.03 exp(i2πz/(0.4 √2))}Pa (z<10m)，i 为虚数单位。实空间单向隐形地毯斗篷的材料参数可由变换声学理论得到。模拟结果表明：当平面波从左侧入射时，由于波矢k 匹配，我们除了镜面反射以外，还可观测到两个强反射分量，从而能够感知地毯斗篷的存在。当平面波从右侧入射时，由于波矢k 失配，系统除了镜面反射以外无其他散射分量从而完美隐身。

图5 (a)宇称时间对称隐形斗篷散射截面与频率关系图(蓝色和红色曲线分别代表左入射和右入射声波的散射截面随频率变化图)；(b)宇称时间对称隐形斗篷散射截面与入射角关系图(入射声波频率为6 kHz且0º入射角对应于左侧入射)

图6 (a)和(b)分别为虚空间中声波左右入射单向隐形地毯斗篷对应的声压场图；(c)和(d)分别为实空间中声波左右入射单向隐形地毯斗篷对应的声压场图(入射声波波长为0.8 m，坐标单位为m，水平方向为z方向)

4 谐振腔场单向局域

这一节中，我们考虑另外一种折射率调制方式的宇称时间对称晶体。该晶体的折射率分布如图7 所示。对于损耗区域，折射率分布为n₁(z) =n₀+ Δn + iΔn ， mL≤z ≤ (m+ 1/4)L 和n₂(z) = n₀ - Δn + iΔn ， (m+ 1/4)L ≤ z ≤ (m+ 1/2)L 。对于增益区域，折射率分布为n₃(z) = n₀ - Δn - iΔn，(m+ 1/2)L ≤ z ≤ (m+ 3/4)L 和n₄(z) = n₀ + Δn - iΔn，(m+ 3/4)L ≤ z ≤ (m+ 1)L 。其中m为整数，从1 取到N，N为宇称时间对称晶体中原胞数； n₀ 为背景媒质折射率； Δn 为折射率实部和虚部调制幅度；L为宇称时间对称晶体原胞长度；z 为沿晶体折射率调制方向坐标轴；i 为虚数单位。L 满足布拉格反射条件，即L = λ/(2n₀) ，其中λ 为波长。基于传递矩阵法，我们可以推导出左右反射系数r_L(R)和透射系数t分别为

其中， M₁₁ ， M₁₂ ， M₂₁ 和M₂₂ 为总传递矩阵的各个元素，M的右上标星号表示共轭操作。通过数值计算，我们发现当原胞数N为特定数值时，可以得到|M₁₁|= |M₂₂|= 1 和M₁₂=M₂₁ = 0 。将其代入公式(5a)—(5c)，则有一维晶体左(右)侧反射率R_L(R)= 0 和透射率T=1。

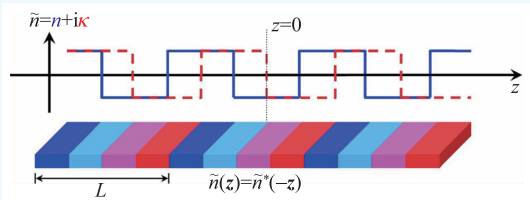
图7 一种宇称时间对称晶体示意图。材料折射率n͂的实部n 和虚部κ沿着z 方向方波调制。其中实部是关于z=0 对称(蓝色实线)，虚部是关于z=0 反对称(红色虚线)。实部和虚部调制之间存在π/2 的相移

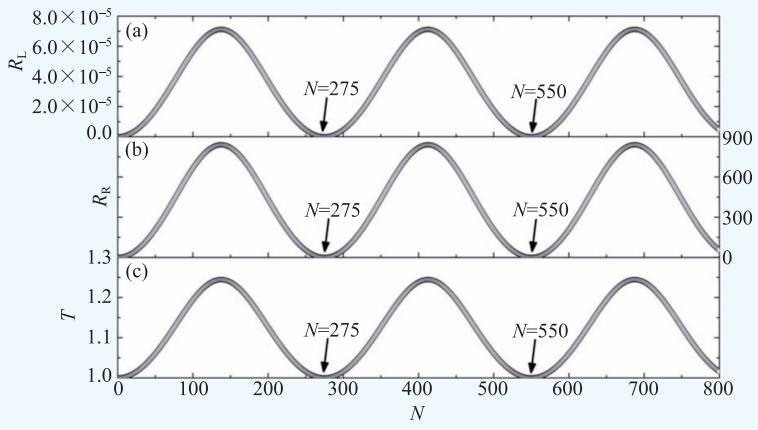
为了验证上述结论的可靠性，我们举一个简单的例子。假设背景媒质折射率n₀ = 3 和折射率实部和虚部调制幅度Δn = 0.2 ，我们分别计算出宇称时间对称晶体的左侧反射率RL ，右侧反射率R_R 和透射率T，如图8 所示，其中宇称时间对称晶体原胞数N从1 变到800。从图8 中，我们发现宇称时间对称晶体的左侧反射率RL 、右侧反射率R_R 和透射率T随原胞数增加发生振荡，且振荡周期为275。数值计算表明宇称时间对称晶体在周期数为275 的整数倍时表现为正反方向均透明。由于该宇称时间对称晶体可以等效于一个提供单向波矢的复声栅，我们在图8 中观测到左侧反射率的振荡幅度( R_L< 7.117 × 10⁵ )要远小于右侧反射率的振荡幅度( R_R < 834 )。

图8 宇称时间对称晶体的左侧反射率(a)，右侧反射率(b)和透射率(c)。宇称时间对称晶体原胞数N从1 变到800

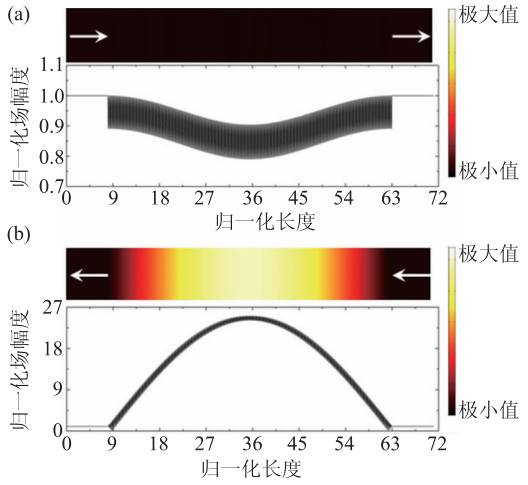
由于宇称时间对称晶体折射率虚部调制关于z=0 不对称(如图7 中红色虚线所示)，正反方向波入射对应的晶体内场分布应不相同。如图9 所示，当宇称时间对称晶体原胞周期数N=275 时，虽然波从左侧或右侧入射，反射均为0 且透射率均为1，但是晶体内场的分布依然能够体现出材料对波的方向响应特性。例如，当波从左侧入射时，场强没有明显的增强效应(图9(a))；但是当波从右侧入射时，场强体现出约3 个数量级的增强效应(图9(b))。干涉条纹类似于法布里—珀罗基频共振。我们还发现正反方向波入射对应的晶体内场分布关于原点都对称，因此场强在增益和损耗媒质中的分布比重各占一半。这时，由增益媒质产生的能量完全被损耗媒质所吸收，最后入射波经过该晶体后不发生衰减。值得一提的是，当入射波频率发生改变时，我们还发现法布里—珀罗共振谐频分量可分为蓝移和红移两支，此时基频并非离散共振频率最低值。对于相同阶蓝移和红移谐振模式，虽然频率不相同，但是场分布极为类似且均为单向局域。

图9 当宇称时间对称晶体原胞周期数N=275 时，波分别从(a)左侧和(b)右侧入射对应的场分布图(图中晶体内波场幅度和晶体长度均相对于入射波幅度和波长进行归一化处理)

5 理想声学传感器件

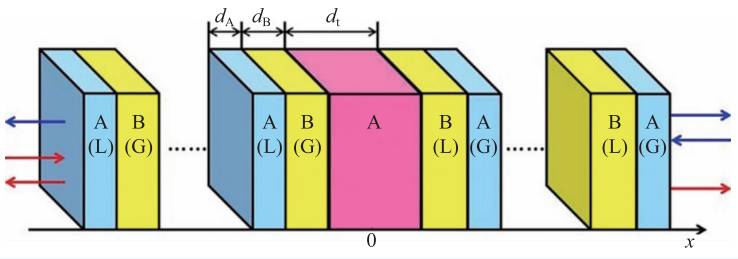
近些年来，弹性波传感器件蓬勃发展。一种简单的弹性波传感方式是基于谐振腔共振。当腔体的长度或材料参数由于温度或者应力等发生细微改变时，弹性波谐振峰会发生明显偏移。该传感方式的灵敏度取决于弹性波谐振峰的Q值，因此提高探测峰的Q值有极大的应用意义。这里，我们设计了一种一维宇称时间对称晶体谐振腔，如图10 所示。A 和B 为两种不同的固体材料。L 和G表示损耗和增益媒质区域。中间红色区域为引入的一个缺陷腔体。固体材料我们选择环氧树脂和硬硅胶。环氧树脂材料参数为：密度1.180×10³ kg/m³，纵波速度2540 m/s；硬硅胶材料参数为：密度1.415×10³ kg/m³，纵波速度948 m/s。

图10 一维宇称时间对称晶体谐振腔示意图(晶体结构参数：d_A=18 mm，d_B=6 mm和d_t=1 mm)

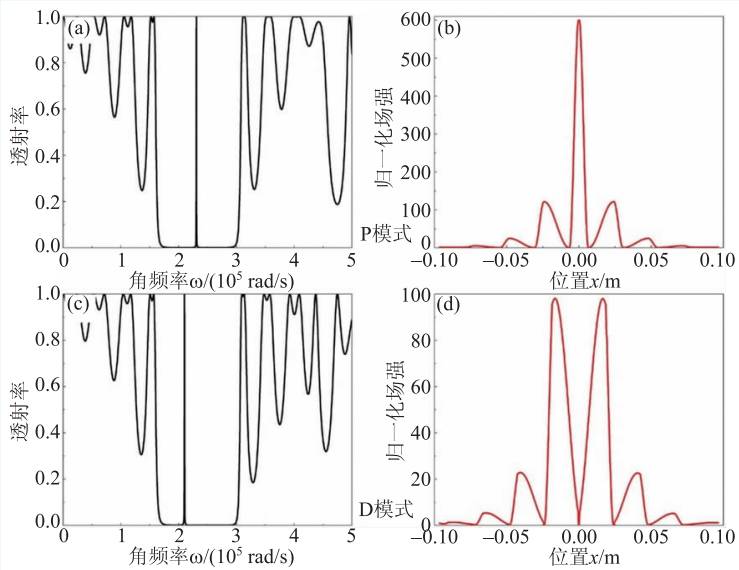
我们首先考虑一种最简单的无损情况，即一般的声子晶体谐振腔结构。当材料A和B分别为环氧树脂和硬硅胶时，声子晶体谐振腔存在P 模式局域态，其透射谱和场分布如图11(a)和(b)所示。P 模式局域场分布特点是场强极大值位于缺陷腔中央且向两侧快速衰减。当材料A和B分别为硬硅胶和环氧树脂时，声子晶体谐振腔存在D模式局域态，其透射谱和场分布如图11(c)和(d)所示。D模式局域场分布特点是场强零点位于缺陷腔中央且向两侧存在两个极大值旁瓣。局域共振P模式和D模式对应的透射谱峰值等于1，频率位置分别位于ω₁ = 2.308 × 10⁵ rad /s 和ω₂ = 2.101 × 10⁵rad /s 。无损系统散射矩阵的本征值谱图如图12(a)和(d)所示，其中局域共振P模式和D模式分别对应于一个本征值两重简并点。

图11 (a)和(b)分别为无损系统中缺陷态P 模式对应的透射谱和位移场分布；(c)和(d)分别为无损系统中缺陷态D模式对应的透射谱和位移场分布

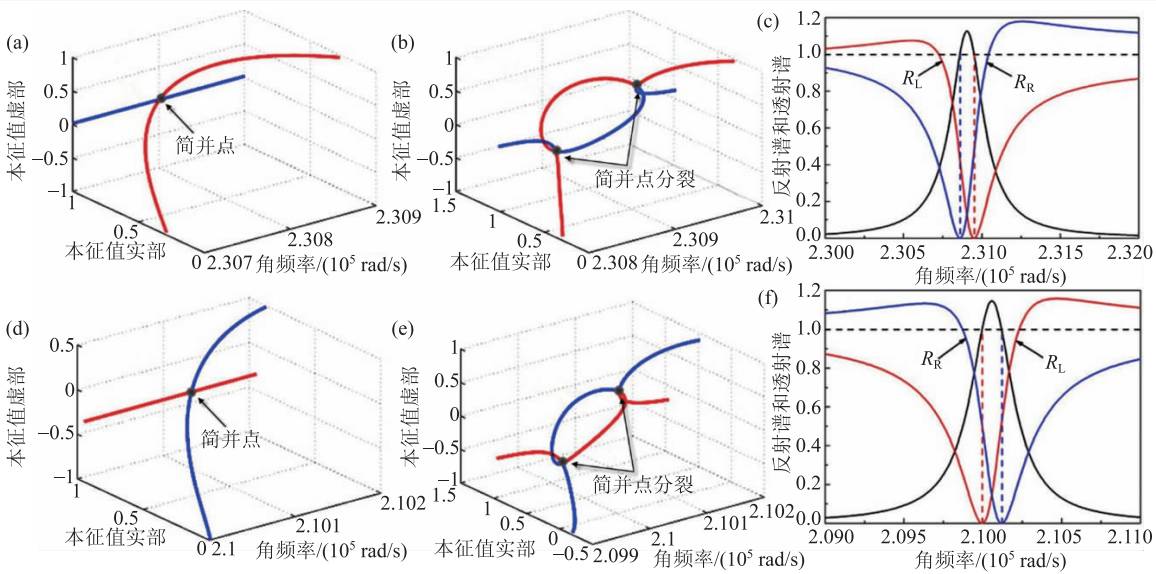
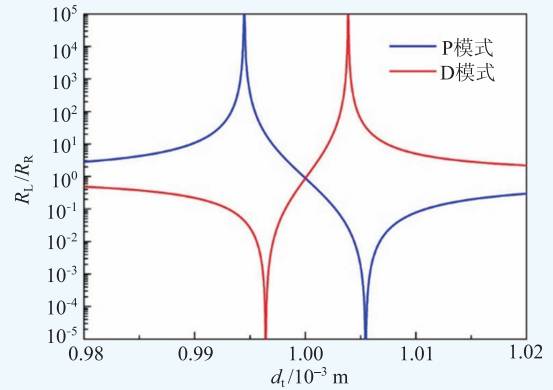
当系统被引入损耗和增益并满足宇称时间对称时，局域共振P模式和D 模式对应的本征值两重简并点发生分裂，变成一对两重简并点，如图12(b)和(e)所示。我们分别计算P模式和D模式对应的透射谱、左侧反射谱(R_L)和右侧反射谱(R_R)，如图12(c)和(f)所示。我们发现，分裂后一对简并点分别对应于系统单向左反射和单向右反射。具体而言，对于P模式，低频简并点对应于单向左反射，高频简并点对应于单向右反射；对于D 模式，低频简并点对应于单向右反射，高频简并点对应于单向左反射。单向反射条件下，根据公式(3)，我们可以得到透射率等于1。利用简并点分裂效应，我们可以进一步设计一种高Q 值声学传感器件。比如，我们将左侧和右侧反射率比值作为一个间接测量物理量。当宇称时间对称系统中缺陷腔体长度dt发生变化时，分裂后一对简并点在频域会发生移动。这样，固定一个探测频率点，我们发现系统状态会依次经过这一对简并点，即从单向左(右)反射转变为单向右(左)反射。如图13 所示，当声学传感系统工作在P 模式下，我们设定工作频率为2.309×10⁵ rad/s。这时，系统随着缺陷腔体长度dt增大，间接测量物理量R_L /R_R从近乎无限大变为0，对应的腔体长度变化量约为11 μm。当声学传感系统工作在D模式下，我们设定工作频率为2.1005×10⁵ rad/s。这时，系统随着缺陷腔体长度dt增大，间接测量物理量R_L/R_R从0 变为近乎无限大，对应的腔体长度变化量约为7.5 μm。通过提高系统增益大小和降低简并点分裂程度，我们可进一步提高宇称时间对称声传感器的灵敏度。

图12 (a)和(d)分别对应无损系统中缺陷态P模式和D模式的系统散射矩阵本征值谱图；(b)和(e)分别对应为宇称时间对称系统中缺陷态P 模式和D模式的系统散射矩阵本征值谱图，其中蓝色实线和红色实线对应于散射矩阵两个本征值；(c)和(f)为宇称时间对称系统中缺陷态P模式和D模式分别对应的透射谱(黑色实线)，左侧反射谱(红色实线)和右侧反射谱(蓝色实线)

图13 宇称时间对称系统中缺陷态P模式和D模式分别对应的左右侧反射率比值R_L/R_R随缺陷腔体长度d_t变化图(该声学传感系统在P 模式下工作频率为2.309×10⁵ rad/s，在D模式下工作频率为2.1005×10⁵ rad/s)

6 未来展望

文章中简单回顾了宇称时间对称声学的一些进展。我们展示了声波和宇称时间对称系统相互作用展现出来的一系列新奇效应，例如单向声隐身、单向声局域和声学系统散射矩阵简并点分裂等。这些效应在无损系统中难以实现且具有理论探索价值和潜在应用前景。目前，宇称时间对称声学大多停留在理论研究阶段，实验实现仍然局限于双单元线性系统。宇称时间对称声学主要受限于声学增益的实现。高维情况下，声学增益已经很难用普通的反馈电路系统来等效实现，而压电材料给我们提供了一种新的可能性。宇称时间对称声学还可与近些年来比较热门的研究领域相互交叉，例如拓扑声学、变换声学、非线性声学和混沌声学，从而衍生出更多的理论研究分支。我们期待未来有更多的理论和实验工作不断发掘和证实声学宇称时间对称系统的奇特性质，并将其应用于现实生活当中。