清华大学崔鹏:探索因果推理和机器学习的共同基础
 图1:崔老师在预讲会直播页面
图1:崔老师在预讲会直播页面
研究背景
 图 2:人工智能技术正从性能驱动走向风险敏感的应用领域
图 2:人工智能技术正从性能驱动走向风险敏感的应用领域
人工智能技术存在的风险
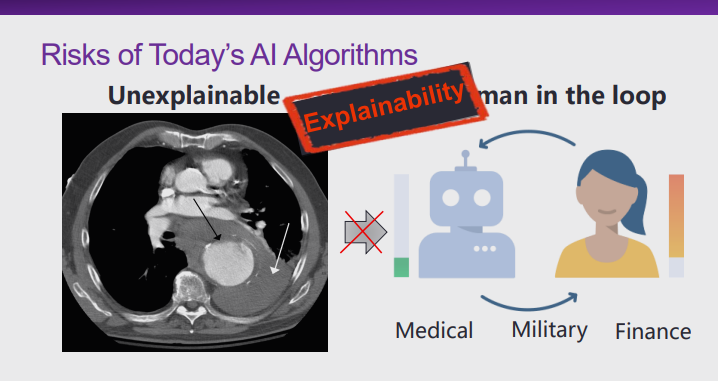 图 3:现有人工智能算法面临的风险——可解释性
图 3:现有人工智能算法面临的风险——可解释性
 图 4:现有人工智能算法面临的风险——独立同分布假设
图 4:现有人工智能算法面临的风险——独立同分布假设
 图 5:图像分类算法面临的风险
图 5:图像分类算法面临的风险
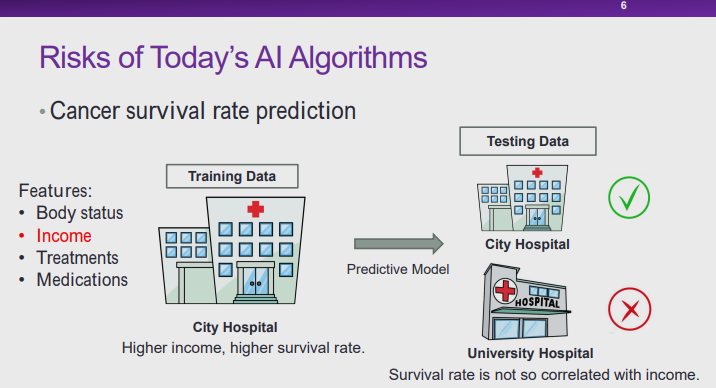 图 6:医疗场景中人工智能算法面临的风险
图 6:医疗场景中人工智能算法面临的风险
机器学习模型面临的困境
 图 7:可解释性与稳定性的困境
图 7:可解释性与稳定性的困境
 图 8:可能的造成窘境的原因——关联
图 8:可能的造成窘境的原因——关联
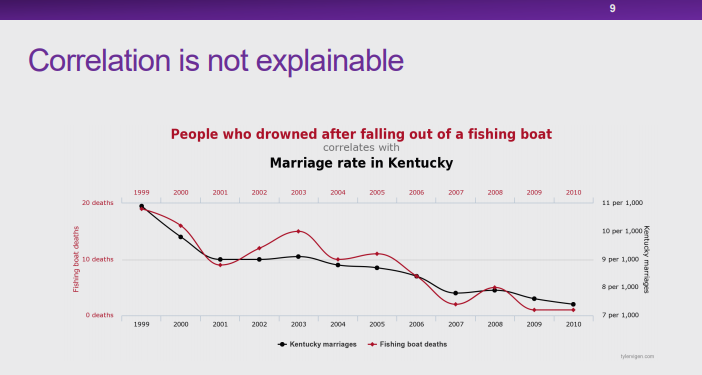 图 9:无法解释的关联性
图 9:无法解释的关联性
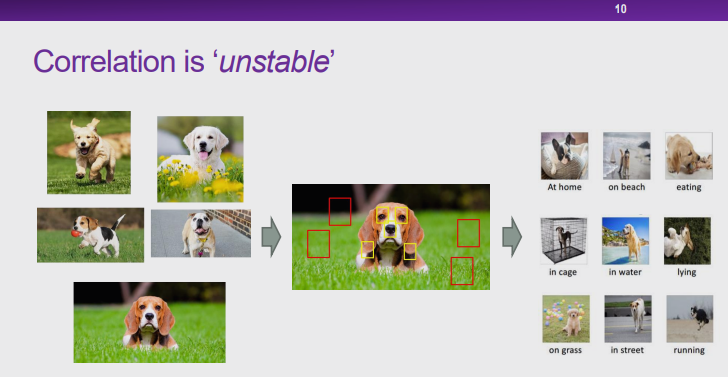 图 10:不稳定的关联性
图 10:不稳定的关联性
使用关联性的正确方式
 图 11:关联性的三个源头
图 11:关联性的三个源头
-
因果: 由于 T 导致了 Y,所以 T 和 Y 有所关联(例如,夏天导致冰淇淋销量上升,则夏天与冰淇淋销量之间存在关联),这种因果机制是稳定且可解释的。 -
混淆 :当 X 会导致 T 和 Y 时,T 和 Y 之间就会产生关联(例如,年龄增长可能会导致人倾向于抽烟,而年龄增长可能也会导致人的体重上升,则抽烟和体重上升之间可能会形成关联)。此时 X 的混淆导致 T 和 Y 产生了关联,这种关联实际上是一种虚假的关联,它不可解释也不稳定。 -
样本选择偏差:如果变量 S 的取值是由T和Y的取值所共同决定,通过控制 S 可以使 T 和 Y 产生关联。在如图 10 所示的例子中,由于存在样本选择偏差(在大多数图片中,狗都在草地上),会使得狗和草地之间会产生关联。从本质上说,这种关联也是虚假关联,是不稳定且不可解释的。
因果与机器学习的结合
 图 12:因果的定义
图 12:因果的定义
 图 13:将因果引入机器学习的好处
图 13:将因果引入机器学习的好处
稳定学习
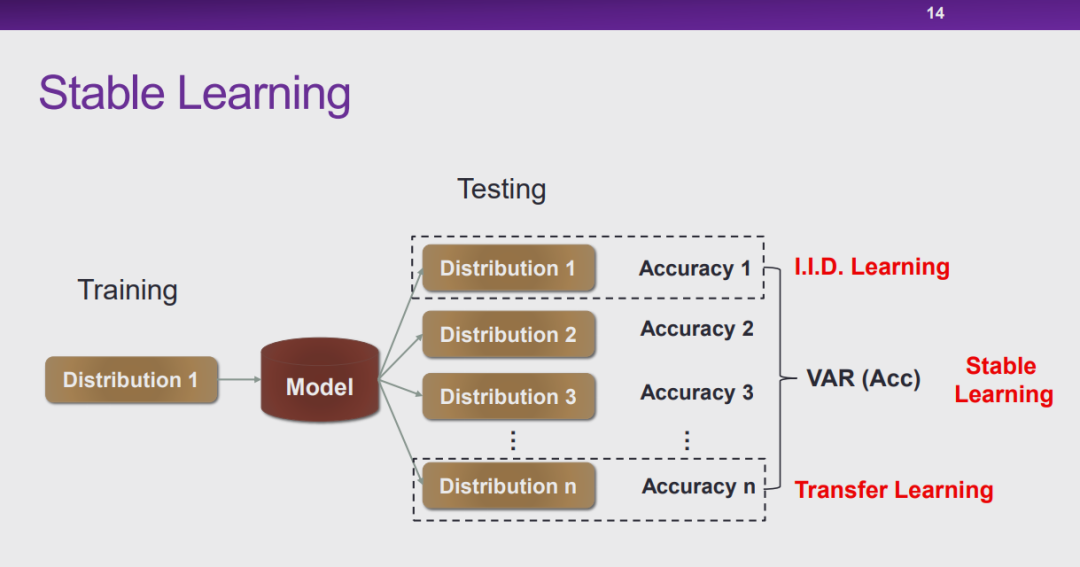 图 14:稳定学习
图 14:稳定学习
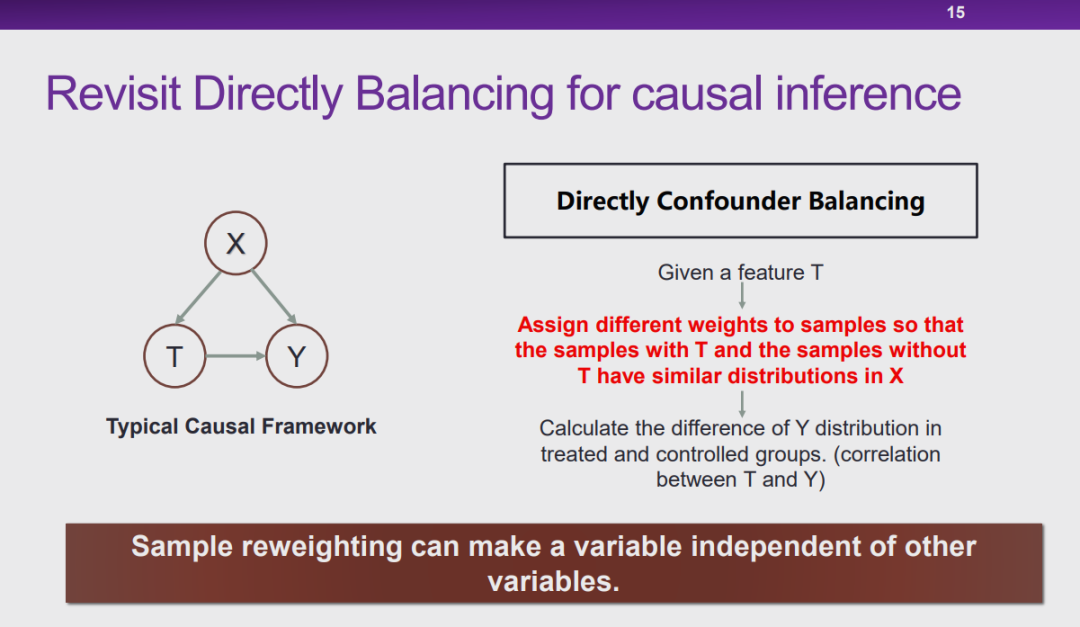 图 15:因果推理的平衡
图 15:因果推理的平衡
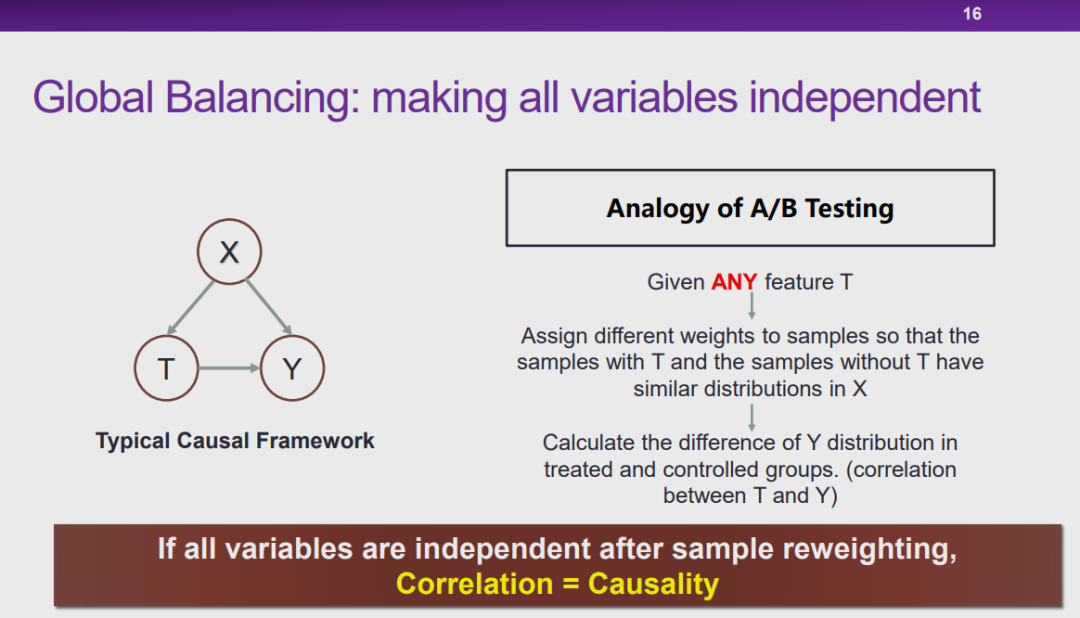 图 16:全局平衡
图 16:全局平衡
理论保障:Stable Prediction across Unknown Environments
 图 17:未知环境下的稳定预测
图 17:未知环境下的稳定预测
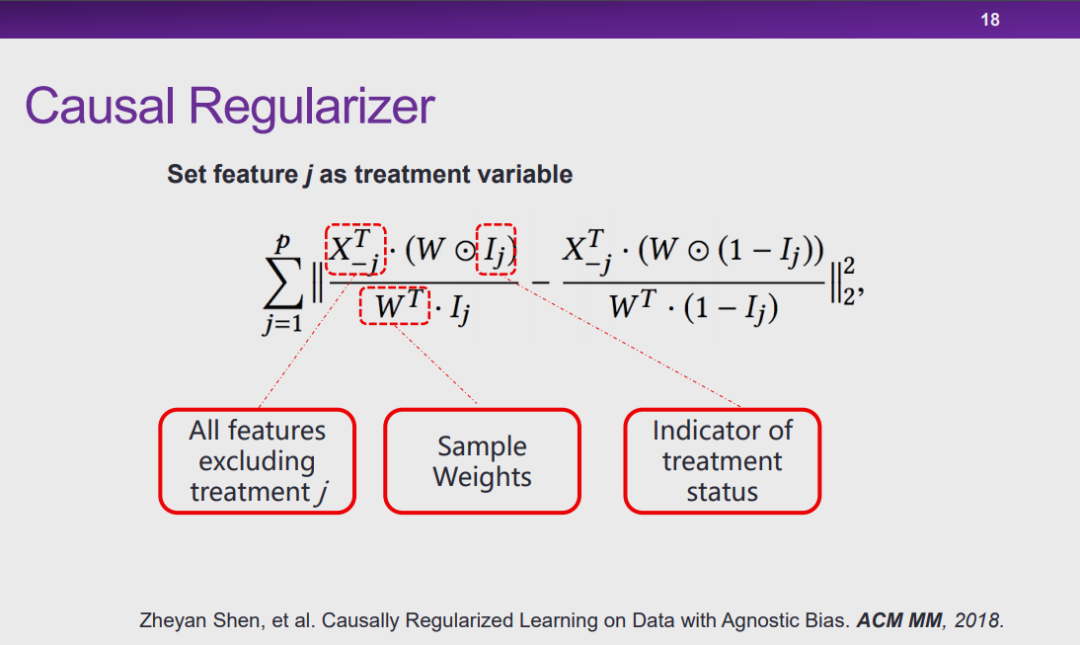 图 18:因果正则化项
图 18:因果正则化项
 图 19:因果正则化的 Logistic 回归
图 19:因果正则化的 Logistic 回归
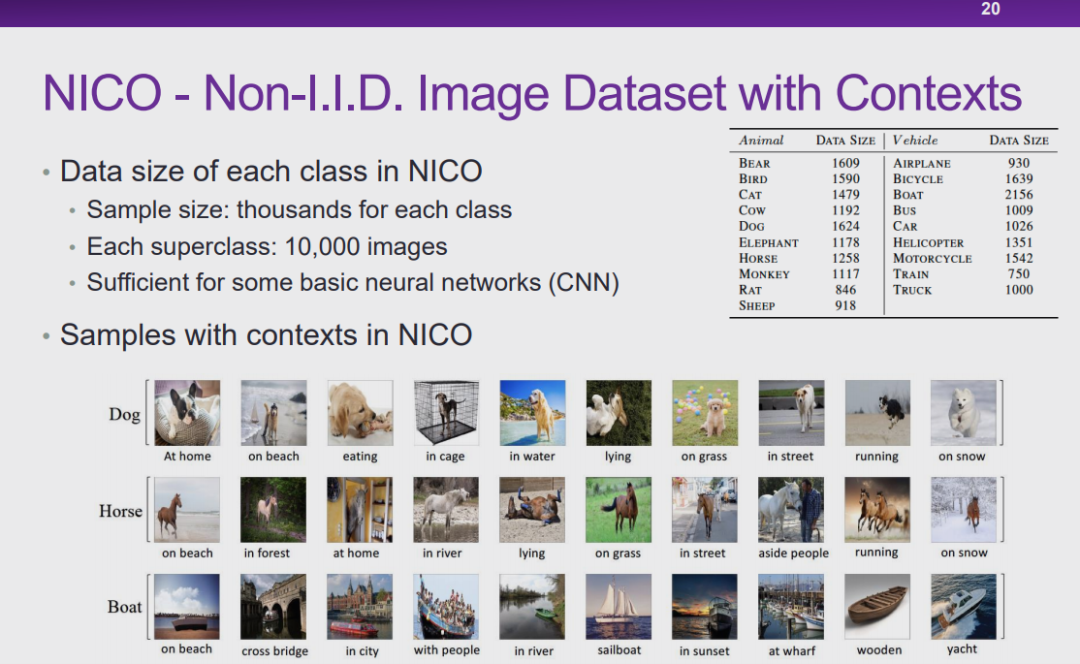 图 20:NICO-具有环境信息的非独立同分布图像数据集
图 20:NICO-具有环境信息的非独立同分布图像数据集
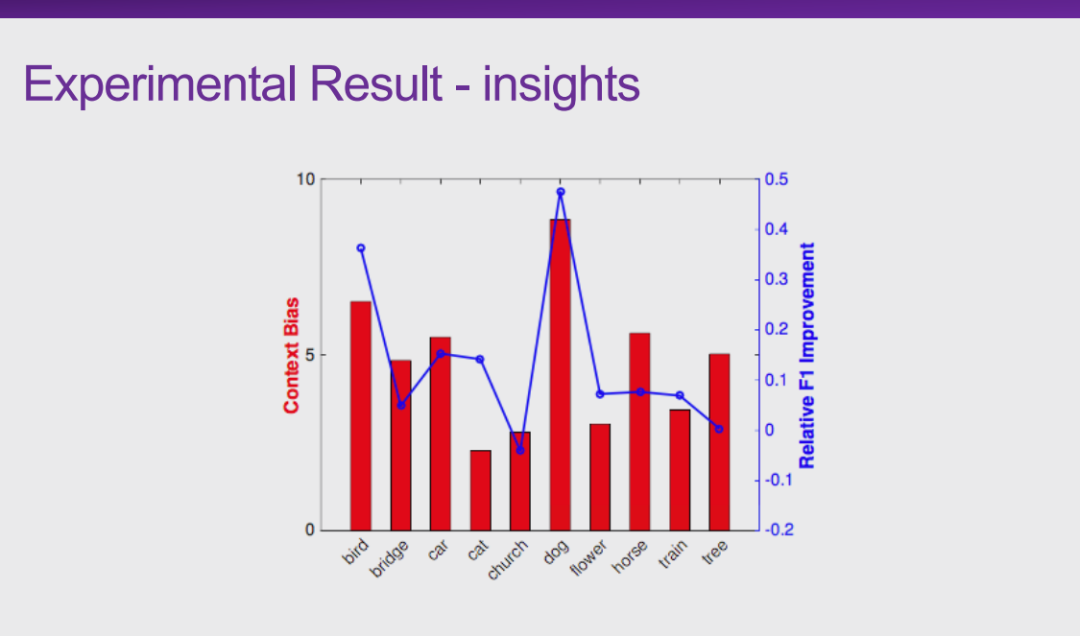 图 21:实验结果——环境偏差
图 21:实验结果——环境偏差
 图 22:可视化结果
图 22:可视化结果
 图 23:连续变量的稳定学习
图 23:连续变量的稳定学习
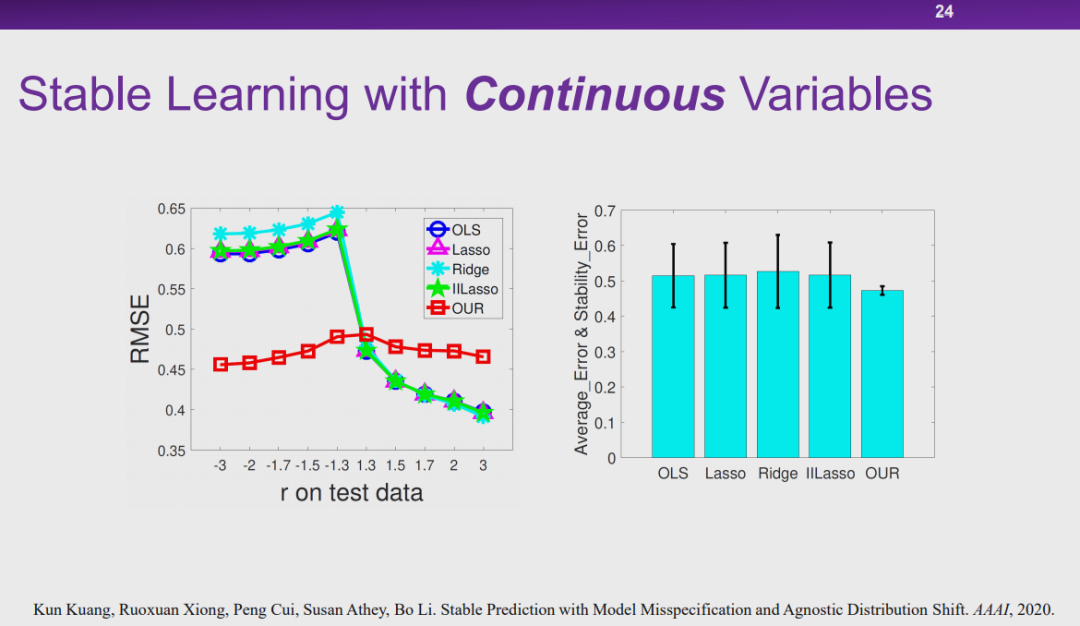 图 24:实验结果
图 24:实验结果
 图 25:差分变量的稳定学习
图 25:差分变量的稳定学习
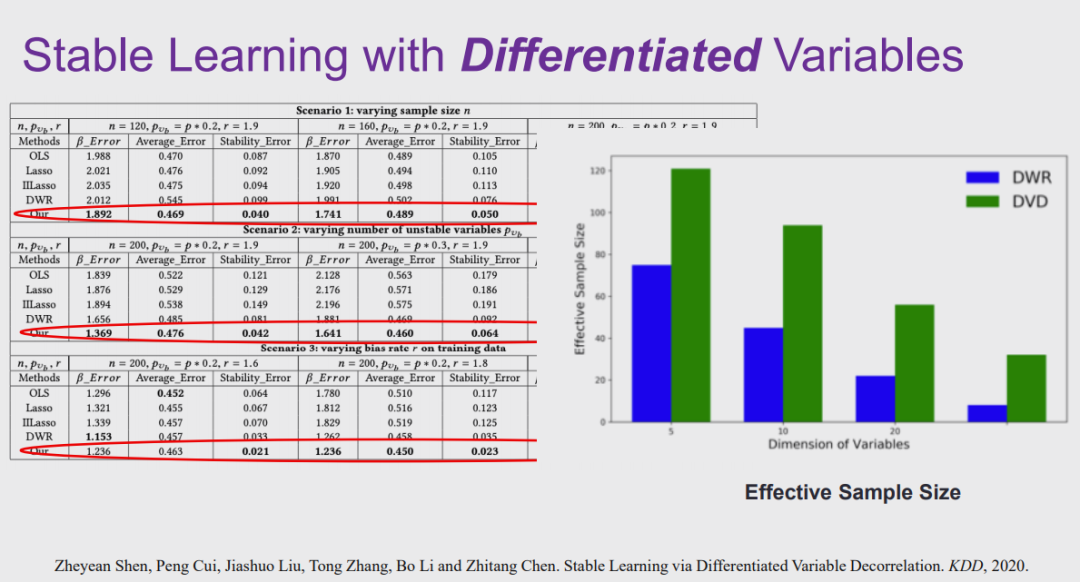 图 26:实验结果
图 26:实验结果
从因果问题到学习问题
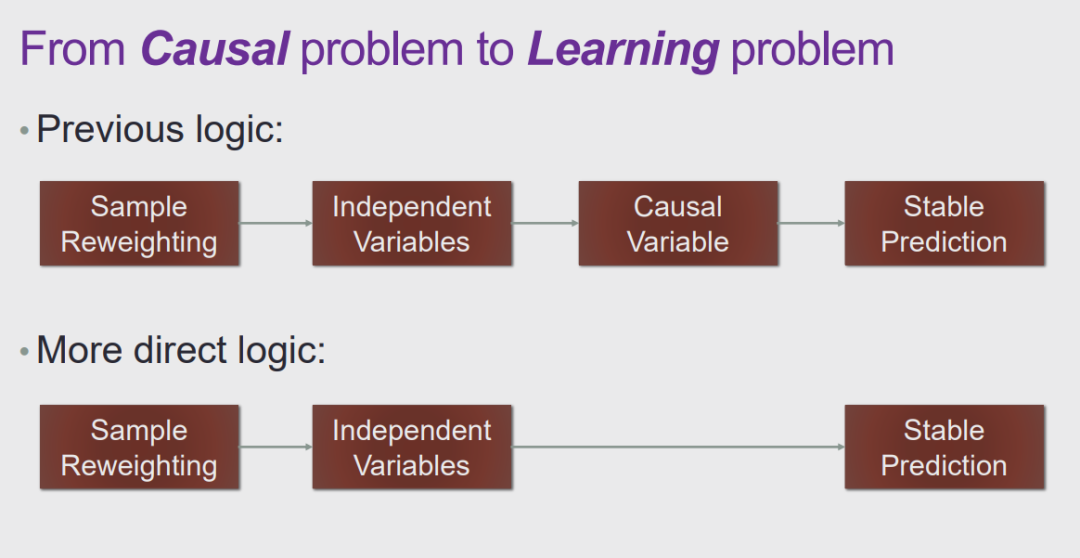 图 27:从因果到学习
图 27:从因果到学习
结语
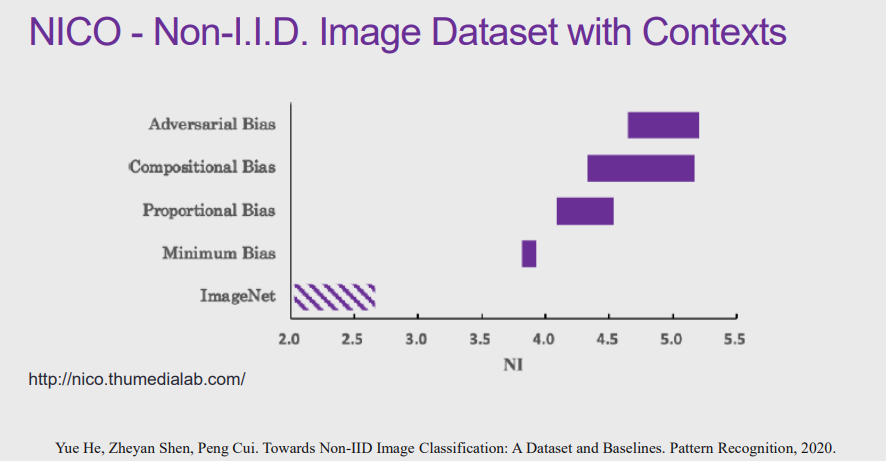 图 28:NICO 数据集
图 28:NICO 数据集
 图 29:引入因果解决当前人工智能技术的局限性
图 29:引入因果解决当前人工智能技术的局限性

点击阅读原文,直达NeurIPS小组!
由于微信公众号试行乱序推送,您可能不再能准时收到AI科技评论的推送。为了第一时间收到AI科技评论的报道, 请将“AI科技评论”设为星标账号,以及常点文末右下角的“在看”。
登录查看更多
相关内容
专知会员服务
126+阅读 · 2019年11月16日
Arxiv
3+阅读 · 2018年5月2日
Arxiv
5+阅读 · 2018年4月25日
Arxiv
5+阅读 · 2018年2月22日
Arxiv
10+阅读 · 2018年1月29日