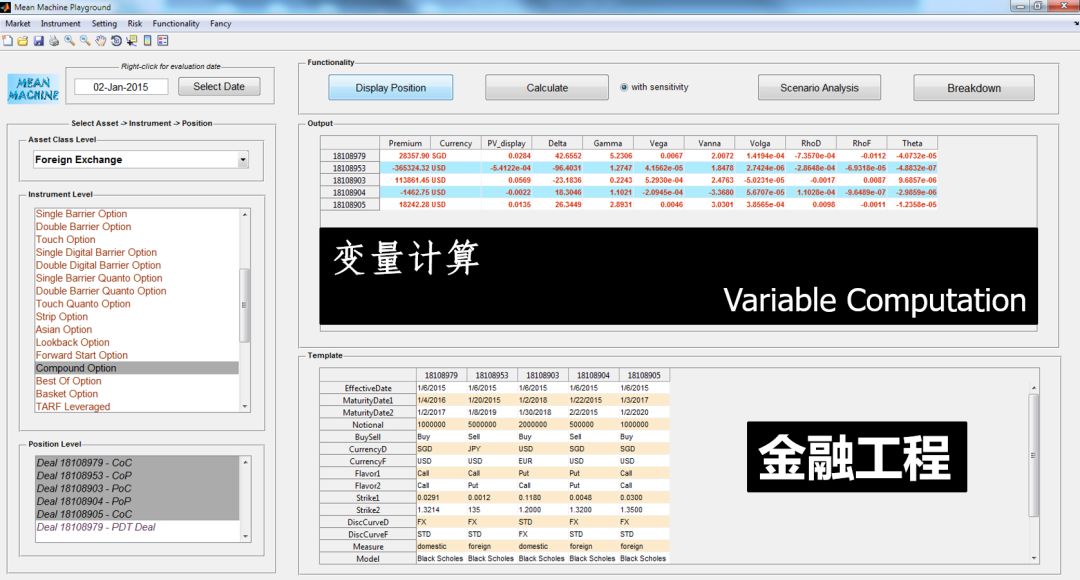
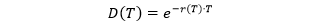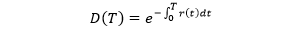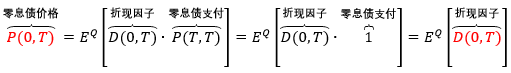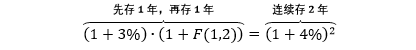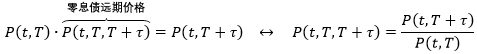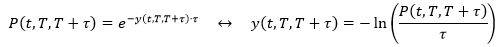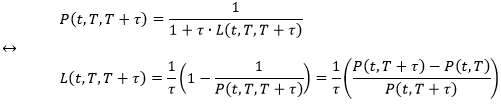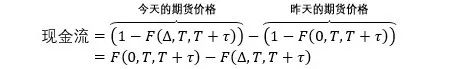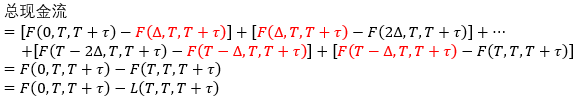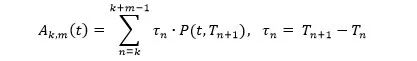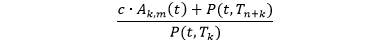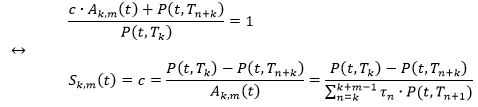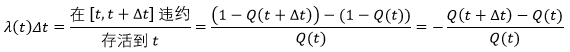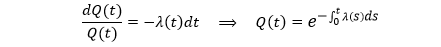『市场基础变量计算』

本文长度为 10812 字，45 图表截屏

建议阅读 56 分钟

0

引言

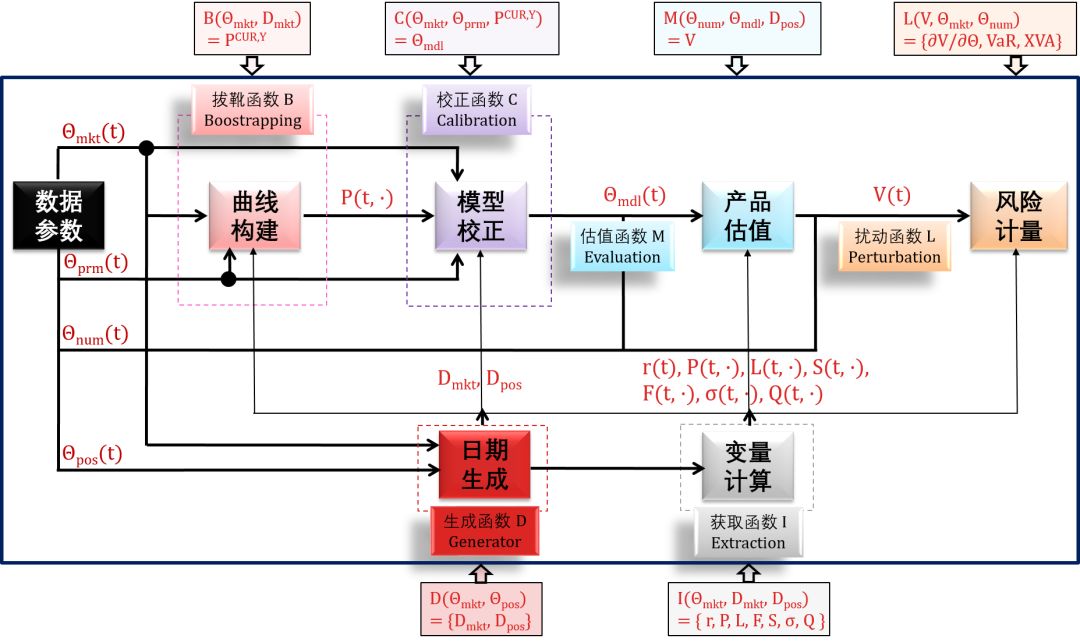
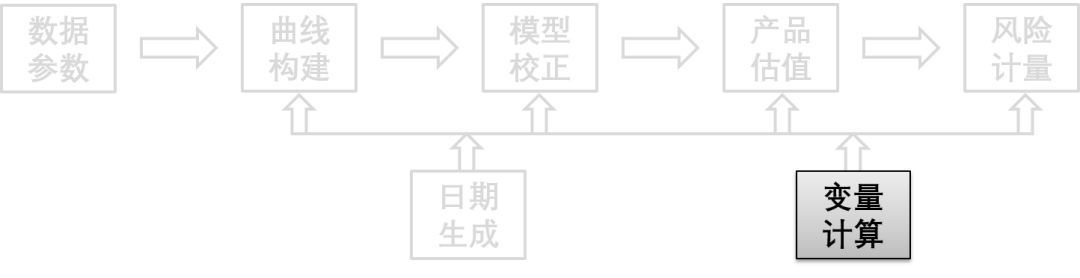
还记得在〖金融工程高度概览〗里的那幅高度浓缩的框架图吗？这里给出更新的版本，新添加了「日期生成」的模块。

整个流程图分为 7 大模块，除了开始的「数据参数」模块，后 6 个模块都有相对应的函数。

 

    模块一：数据参数

    模块二：日期生成 (生成函数 D)

    模块三：变量计算 (获取函数 I)

    模块四：曲线构建 (拔靴函数 B)

    模块五：模型校正 (校正函数 C)

    模块六：产品估值 (估值函数 M)

    模块七：风险计量 (扰动函数 L)

当时还下里巴人的作诗一首：

 

    数据参数最重要，没有它们没有料。

    日期生成累不爱，细节处理定成败。

    变量计算贯全场，各步所需用处广。

    曲线构建排最前，所有产品需折现。

    模型校正剔主观，优化函数来调参。

    产品估值有三法，通用一切看蒙卡。

    风险计量重之重，对冲风控用之用。

本篇是金融工程系列的第五篇 (第六篇已经写了)，总体内容如下：

1. 弄清量化金融工程十大话题-上

2. 弄清量化金融工程十大话题-下

3. 金融工程高度概览

4. 日期生成

5. 变量计算

6. 模型校正

7. 曲线构建 - 单曲线环境

8. 曲线构建 - 多曲线环境

9. 产品估值理论

10. 产品估值 - 解析法和数值积分法 (CF)

11. 产品估值 - 偏微分方程有限差分法 (PDE-FD)

12. 产品估值 - 蒙特卡洛模拟法 (MC)

13. 风险计量 - 敏感度 (Greeks & Sensitivities)

14. 风险计量 - 风险价值 (VaR)

15. 风险计量 - 价值调整 (XVA)

我的天，这个系列写完又是可以写书的节奏，忙死我吧 。

---

言归正传，题目里的变量指的是金融市场的基础市场变量 (fundamental market variable)，之后就简称为变量。常见的变量包括

1. 利率 (interest rate) 
   

2. 汇率 (exchange rate)
   

3. 价格 (price)

4. 波动率 (volatility)
   

5. 信用价差 (credit spread)

利率、汇率、价格和信用价差都是时间 T 的函数，因此这些变量 (用 X 代表) 都是以曲线 (curve) 的形式呈现。

    X(T₁), X(T₂), ..., X(T_n)

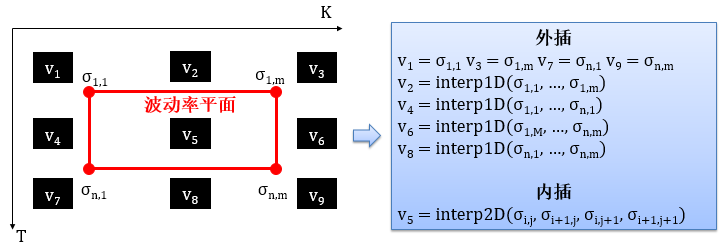
波动率是时间 T 和行权价格 K (或者价内水平 moneyness) 的函数，因此波动率都是以平面 (surface) 的形式呈现。【特例：掉期波动率是以立体 (cube) 的形式呈现，后面详细介绍】

    σ(T₁, K₁), σ(T₂, K₁), ..., σ(T_n, K₁)

    σ(T₁, K₂), σ(T₂, K₂), ..., σ(T_n, K₂)

        ...

    σ(T₁, K_m), σ(T₂, K_m), ..., σ(T_n, K_m)

在金融市场中，在一些标准时点 (standard tenor) 和 (或) 标准价内水平上，每天有各式各样利率、远期、信用基差和波动率的市场报价 (market quote)。

但在估值金融产品时，我们需要非标准时点和 (或) 非标准价内水平上利率、远期、信用基差和波动率的值，而本帖的变量计算就是讲这个事情。

本帖的目录如下：

目录

第一章 - 利率

    1.1 直观理解

    1.2 真实操作

第二章 - 汇率

    2.1 直观理解

    2.2 真实操作

第三章 - 价格

    3.1 直观理解

    3.2 真实操作

第四章 - 信用价差

    4.1 直观理解

    4.2 真实操作

第五章 - 波动率

    5.1 直观理解

    5.2 真实操作

第六章 - 插值

    6.1 具体例子

    6.2 插值方式

总结

1

利率

1.1

直观理解

我们把 100 元钱存在银行里，一年后如果银行给我们 103 元钱，那么多出的 3 元叫做利息，即 100 元「生」出来的钱。利息除以本金就是利率 （interest rate）。

    利率 = 利息/本金 = 3/100 = 3%

那么这个利率是根据什么确定的呢？你的本金是钱，而钱 (货币) 也是一种商品，也有自身的价格，这个价格就是利率。想想你是不是听过「利率高了钱就贵了」这类的话。

利率作为钱的价格，其水平是由市场供求关系决定的。此外，利率水平还受其他一些因素影响，比如风险程度、贷款期限、借贷人信用状况、通胀水平和政治因素等。在全球金融市场联通的今天，一国的利率水平还受别的利率水平的影响。

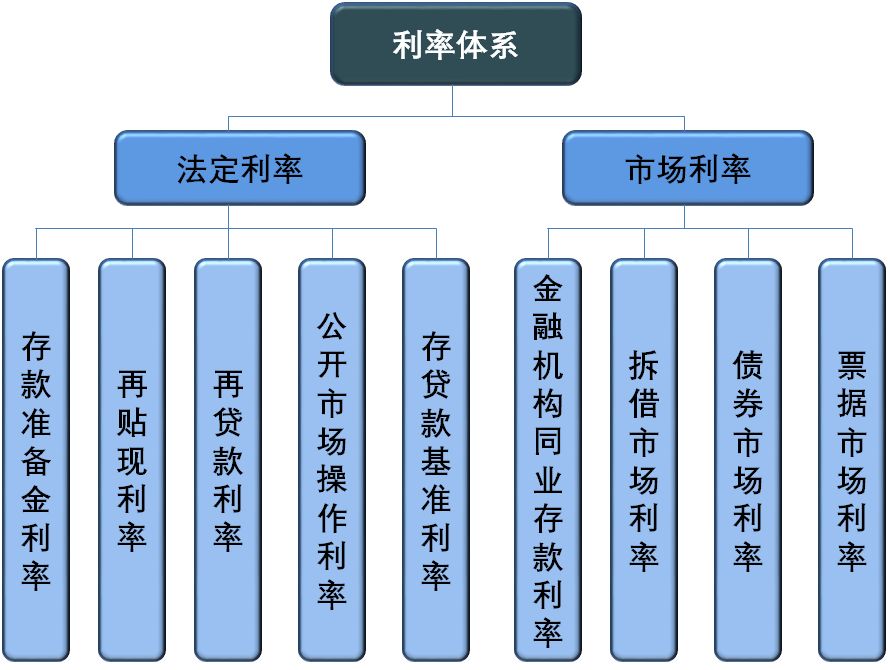
下图展示了在中国市场上的利率体系。

计算利息的方法有两种，单利 (simple interest) 和复利 (compounding interest)。

• 单利只在本金上计算利息，所得的利息不再加入本金重新计算利息。比如你存 100 元，年利率是 3%，那么一年之后你得到 103 元 (3 元是利息)，两年之后得到 106 元 (6 元是利息)

• 复利不光本金要计算利息，本金生出来的利息也要计算利息。比如你存 100 元，年利率是 3%，那么一年之后你得到 103 元 (3 元是利息)，两年之后得到 106.09 元 (6.09 元是利息)。比单利多出来的 0.09 元是第一年的利息 3 元在第二年也做了本金用来计算利息。
  

Compound interest is the eighth wonder of the world. -- Albert Einstein

利率是资金使用的价格，它的涨跌关系着个人、企业和政府的钱袋。对个人，当存款利率水平高，老百姓会把收入存储起来日后再消费 (延迟满足感 )。对企业，当贷款利率水平变动，会影响企业为了经营而借钱要支付的利息。

知识点 - 折现

当我们把未来的钱折算成今天价值的时候，就需要折现率 (discount rate) 或折现因子 (discount factor) 的概念了。

比如，目前利率是 3%，那么今天的 100 元就相当于明年的 103 元，因为我们可以这 100 元贷出去而明年拿到 103 元。同理，明年 103 元只能相当于现在的 100 元，那么这个 3% 就是折现率。

    100 × (1+ 3% ) = 103

或者，我们说 1/(1+3%) = 0.97 是折现因子

    103 *  0.97 = 100

不难看出，利率 (折现率) 越高，折现因子越低，因此折现后的收入越低。

折现的方式有两种，用按年复利 (annually compounding) 来举例：

• 单利折现因子 = 1/(1+T×r)

• 复利折现因子 = 1/(1+r)T

其中 r 是年化利率，即一年能享受到的利率，T 是年限，即年的倍数。如果按半年复利 (semiannually compounding) 来计算折现因子会有什么变化呢？将利率 r 除以 2，将年限 T 乘以 2。

• 单利折现因子 = 1/(1+2T×r/2)

• 复利折现因子 = 1/(1+r/2)2T

我们发现单利折现因子不变，但复利折现因子变大了。按季度复利 (quarterly compounding)、按月复利 (monthly compounding) 和按天复利 (daily compounding) 就不写了，直接跳到连续复利 (continuously compounding) 的折现因子。

    折现因子 = exp(-r×T)

要推出上面表达式，将 1/(1+r/m)mT 在 m → ∞  时取极限即得到。

在金融工程里，相比于折现率，我们用连续复利下的折现因子更多些。

1.2

真实操作

折现因子

折现因子 (discount factor) 就是把「未来 T 时点的现金流折算成 0 时点 的现值」的一个数。

金融工程里通常用 D(0, T) 或 D(T) 来表示折现因子，它通常在 0-1 之间。现在一些国家都有负利率，D(T) 也可以大于 1，最终我们有 D(T) ＞0。

下面公式写出连续复利下的折现因子 D(T) 和利率 r(T) 之间的关系。

上面假设利率 r(T) 在 0 到 T 之间是常数，不是随机的。

零息债价格

在 0 到 T 之间，如果利率 r(t), t ⊂ [0, T] 是一个随机变量，那么对应的折现因子也是随机的。这时折现因子 D(T) 和利率 r(t) 之间的关系为

这样在用折现因子计算产品价值时会得到一个随机的结果，这不是我们希望看到的。

因此我们需要一个确定的“折现因子”来折现现金流，它就是零息债价格 (zero-coupon bond price, ZCB price)，用 P(0, T) 或 P(T) 来表示，它等于折现因子在「风险中性」测度下的期望。

知识点 - 零息债价格和折现因子

零息债是一种金融产品，它在到期日 T 时的支付为 1，即 P(T, T) = 1，现在要计算它的现值 P(0, T)。在风险中性 (risk-neutral) 测度下

上式首尾一看，发现 P(0, T) 是 D(0,T) 在风险中性测度 Q 下的期望。

很多人会把两者混淆，当利率是常数或确定时，两者一样；当利率是随机时，两者不同，零息债价格是折现因子的期望。

到期日并不唯一，因此市场上会有多个零息债价格组成一条曲线。之后我们在构建曲线时说的折现因子，指的都是零息债价格。切记！切记！切记！

零息利率

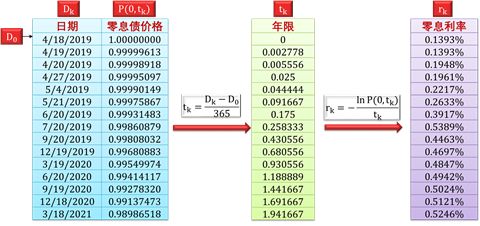
零息利率 (zero rate) 是到期日为 T 的零息债券在 0 到 T 之间的收益率。

和零息债价格一样，不同到期日下有不同的零息利率。一般来说，零息利率的曲线比零息债价格的曲线传达的可视信息会更多些。

• 后者 P(T) 随着 T 是递减的
  

• 前者 r(T) 随着 T 通常递增，但也可能先增后减

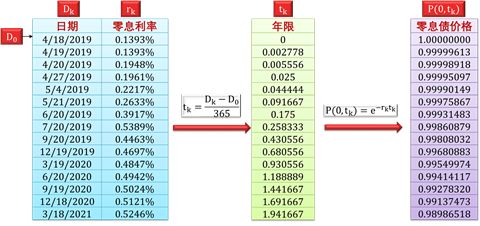
下面两图分别说明如何从 P(T) 计算出 r(T)，和从 r(T) 计算出 P(T)。

远期利率

上节介绍的利率都是从现在开始的利率，称即期利率 (spot rate)，而远期利率 (forward rate) 是隐含在给定的即期利率中从未来的某一时点到另一时点的利率水平。

一个简单的例子，就是银行有 1 年和 2 年的定存利率 3% 和 4%，那么我们将 1000 元存一年，到期的收益为

    1000 × (1+3%) = 1030

如果存两年，到期的收益为

    

    1000 × (1+4%)2= 1081.6

假设你存完一年再继续存一年，得到的收益应该和连续存两年一样多。根据利率的定义 (利息/本金)，计算从一年到两年这段时期的 (远期) 利率为

    (1081.6 - 1030)/1030 = 5%

或者用公式

将上式两边求倒数

写出上式的通用表达式得到

    P(0, 1) · P(0, 1, 2) = P(0, 2)

其中

• P(0,1) 是在 0 时点观测到期 1 年的零息债价格

• P(0,2) 是在 0 时点观测到期 2 年的零息债价格

• P(0,1,2) 是在 0 时点观测到期 2 年但 1 年后的零息债远期价格

把 1 年和 2 年用 T 和 T+τ 代替 (τ 可看成是远期债的期限)，把 0 时点用 t 代替，我们得到一个更为通用的公式。

其中 P(t, T, T+τ) 是在 t 时点观测的在 [T, T+τ] 一段内的零息债远期价格。再用它推出连续复利型的远期利率 y(t, T, T+τ)

但在实际市场报价中，离散型的远期利率 L(t, T, T+τ) 最常见

这个 L(t, T, T+τ) 就是大名鼎鼎但 2021 年就要消失的 LIBOR，对于不同市场，τ = 1 个月、3 个月、6 个月和 1 年。

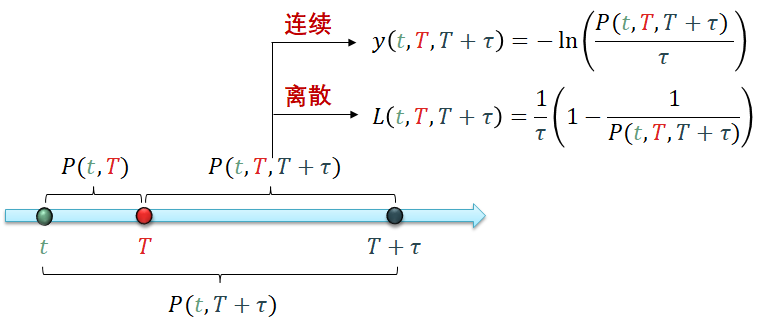
用下面一张图来总结远期利率 (远期零息债价格) 之间的关系。

期货利率

在 Eurodollar 期货市场上，期货投资者在到期日 T 可得

    1 - L(T, T, T+τ)

在 0 时点，投资者不需要花费便可进入该期货，但是在时点 T 要付

    1 - F(0, T, T+τ)

来换取 1 - L(T, T, T+τ)。这里 F(t, T, T+τ) 是 t 时点观测的在 [T, T+τ] 期间的期货利率 (futures rate)。

实际上，期货利率是每天盯市 (mark-to-market) 而结算。对于 ∆ = 1 天，期货持有者的现金流为

按着上面的盯市过程至到期日 T，期货持有者经历的总现金流为

在到期日时远期利率 L(T, T, T+τ) 必须要等于期货利率 F(T, T, T+τ)，要不然会有套利机会。

1. 当利率上涨，每天现金流为负，期货亏钱，投资者需要向交易所付钱结算。雪上加霜的是，融资代价随着利率上涨变大了。

1. 当利率下跌，每天现金流为正，期货赚钱，投资者可以再投资盈余的钱。但是，收益率随着利率下跌变小了。

在盯市过程中，期货投资者受着「高融资成本」和「低再投资收益」的双重魔咒，那么它们必须要求合约的期货利率 (需要每天盯市结算) 要大于远期利率 (不需要每天盯市结算)。

至于如何计算期货利率，这个需要建模来计算凸性调整 (convexity adjustment)，先略去不讲。

远期掉期利率

介绍远期掉期利率 (forward swap rate) 之前，我们先介绍年金 (annuity)。对于年金，首先又要定义它现金流发生的期限结构 (tenor structure)。

    0 ≤ T₀ < T₁ < ... < T_N

在时点 T_k 和 T_m 上 (其中 k, m 和 k+m 都在 0 和 N 之间)，定义年金 A_k,m

考虑 T_k < T_k+1 < ... < T_k+m 上的固息债 (息率为 c)，它在 T_k 时点的远期价格为

远期掉期利率就是这样的一个息率 (用 S_k,m 表示) ，使得 T_k 时点的远期价格为 1。

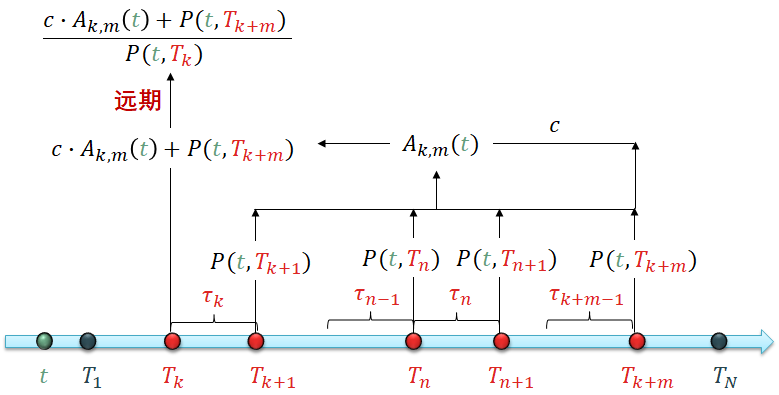
用下面一张图来总结年金和多个到期日的零息债价格之间的关系。

2

汇率

2.1

直观理解

在国内商店买东西，你会很自然的使用人民币，因为人民币是中国的法定货币。但假如你去美国旅游去买东西，你需要支付美元，因为美元是美国的法定货币。那么在出国之前，你需要用人民币“购买”一些美元，购买 (兑换) 美元的价格就是人民币兑美元 (CNYUSD) 的汇率 (exchange rate)。

汇率的表示方法有两种：

1. 直接标价法：1 单位的外币等于多少单位的本币。

2. 间接标价法：1 单位的本币等于多少单位的外币。

按 2019 年 6 月 27 日的 USDCNY 是 6.88，指 1 美元可以兑换 6.88 人民币，如果

• 后一天的 USDCNY 是 6.9，汇率涨，1 美元换更多的人民币，美元升值，人民币贬值。

• 后一天的 USDCNY 是 6.85，汇率跌，1 美元换更少的人民币，美元贬值，人民币升值。

如果说利率是货币的绝对价格，那么汇率是两种货币之间的相对价格，它反映了不同货币的购买力 (purchasing power)。

汇率 (外币/本币) 的升降主要受以下四个因素的影响：

进出口差额：出口是把本国的商品和服务卖给外国，收汇；进口是购买外国的商品和服务，付汇。

• 当出口额大于进口额，出现贸易顺差，外币需求少供给多而贬值，本币升值，汇率下跌。

• 当出口额小于进口额，出现贸易逆差，外币需求多供给少而升值，本币贬值，汇率上升。

资本出入差额：道理和进出口差额类似。

• 当资本流入大于流出，出现资本项目顺差，外币需求少供给多而贬值，本币升值，汇率下跌。

• 当资本流入小于流出，出现资本贸易逆差，外币需求多供给少而升值，本币贬值，汇率上升。

利率差异：导致资本流出流入。

• 当本国利率高于外国利率，会有资本流入，兑换成本币获取更高的利息，本币需求多而升值，外币贬值，汇率上升。

• 当本国利率低于外国利率，会有资本流出，兑换成外币获取更高的利息，外币需求多而升值，本币贬值，汇率下跌。

通胀率差异：导致购买力下降上升。

• 当本国通胀率高于外国通胀率，本币购买力下降而贬值，汇率下跌。

• 当本国通胀率低于外国通胀率，本币购买力上升而升值，汇率上升。

此外，人们的心理预期也会影响着汇率，比如人民认为某个国家的政局不稳而会抛售该国货币 (贬值)。政府的干预也会影响着汇率，比如 1985 年美元升值加剧美国贸易赤字，美国联合西方强国达成「广场协议」一起拿出 200 亿美元投入外汇市场购买日元，结果美元狂跌日元狂涨。

2.2

真实操作

知识点 - 外汇即期

在一个外汇即期 (FX spot)，两个交易对手同意将一笔外币金额和一笔本币金额兑换，兑换的汇率是即期汇率 (spot FX rate)，而结算日通常在交易日后两个工作日 (取决于货币对)。

知识点 - 外汇远期

在一个外汇远期 (FX forward)，两个交易对手同意将一笔外币金额和一笔本币金额兑换，兑换的汇率是远期汇率 (forward FX rate)，而结算日时双方同意的一个日期。

在外汇市场，即期汇率每天都有市场报价，如下 10 个货币对的即期汇率。

而远期汇率是我们需要计算的，它的计算方法很简单，在某个到期日 T，远期汇率等于即期汇率加上相对应的掉期点 (swap point)。

    F(0, T) = S + sp(T)

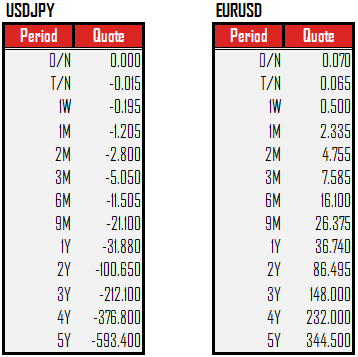
其中 S 是即期汇率，F(0, T) 是 T 期限的远期汇率，sp(T) 是 T 期限的掉期点。掉期点也有市场报价。如下给了 USDJPY 和 EURUSD 的从隔夜 (O/N) 到五年 (5Y) 的掉期点。

但是掉期点不能直接加在即期汇率上，而是先除以一个因子再加，这个因子随货币对而异，USDJPY 的因子是 100，EURUSD 的因子是 10000。现在假如我们要计算 1Y 的 USDJPY 远期汇率和 3Y 的 EURUSD 远期汇率。

    F_USDJPY(0, 1Y) = S_USDJPY+ sp(1Y)

                            = 107.69 - 31.88/100

    

    F_EURUSD(0, 3Y) = S_EURUSD+ sp(3Y)

                            = 1.137 - 148/10000

3

价格

3.1

直观理解

价格 (price) 是一项以货币为表现形式，为商品所订立的价值数字。前两节已经讨论了利率和汇率，它们把货币本身当做商品，因此它们也是特殊的“价格”

• 利率是货币的绝对价格 (无单位)

• 汇率是两个货币间的相对价格 (无单位)

对于其他商品，比如股票、商品，那么价格就是用货币交换一个单位商品所需的货币量多少，比如

• 1 股腾讯股票的价格为 352 港币 (单位是港币)

• 1 克纯度 99.99 的上海金的价格为 315 人民币 (单位是人民币) 

3.2

真实操作

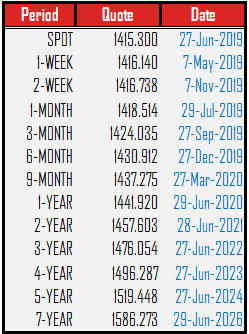
商品的市场报价是不同到期日的商品远期价格，下图展示黄金远期的报价，第一行 Period 是 Spot 对应的报价是黄金的即期价格。

股票的市场报价只有即期价格 (spot price)，它的远期价格可以由套利关系计算出来 (为了简便，假设股票没有支付红利)。在远期合约中，一方在未来某一个约定时间点按约定价格像另一方出售约定数量的股票，那么这个约定价格是多少。

• 考虑远期合约的卖方，他有义务在到期日 T 向卖方出售股票。他可以在签订合约是借入 S(0) 用于购买股票，等待着到期日以约定价格卖给买方，与此同时，他需要支付借钱买股票的本和利息 S(0) · erT。如果约定价格少于 S(0) · erT，卖方会蒙受损失。

• 考虑远期合约的买方，他有义务在到期日 T 从卖方购买股票。他可以在签订合约是做空卖出 S(0) 得到一笔钱，存在无风险账户中，等待着到期日从卖方以约定价格买入股票，与此同时，他享受着本和利息 S(0) · erT。如果约定价格高于 S(0) · erT，买方会蒙受损失。

综上所示，约定价格为 S(0) · erT，其中 S(0) 是股票即期价格，r 是无风险利率，T 是远期到期日。将上面结论推广一下，股票带红利率 q 的远期约定价格为 S(0) · e(r-q)T。

4

信用价差

4.1

直观理解

债券 (bond) 和信用违约掉期 (credit default swap, CDS) 是信用市场中的最基础的产品，两者都有自己的信用价差 (credit spread)。

债券就不用多解释了，它的信用价差是用以向投资者补偿参照资产违约风险的、高于无风险利率 r_riskless 的利差 s。那么债券的收益率 r_riskless 为

    r_risky(T) =  r_riskless(T) + s(T)

再了解 CDS 的信用价差之前，先了解下 CDS。

知识点

信用违约掉期是一种互换合约，其中保护买方 (protection buyer) 从保护卖方 (protection seller) 获取一份担保，其担保是在发生一件预先定义的信用事件时，保护买方能够从保护卖方索取因该事件而导致的损失。为此，保护买方必须定期付一笔保费给保护卖方。

CDS 中保护买方付的保费率就是 CDS 的信用价差。 

---

给定一个 3 年到期企业债券，假设它在的收益率是 (bp = basis point，基点)

    r_riskless + 60 bp

那么按理来说，用它做标的的 3 年 CDS 的信用价差也应该是 60 bp。这样对于 CDS 的保护买方，这个 CDS 可以由一个多头企业债券 (有信用风险) 和一个空头国债 (无信用风险) 来复制。

但在实际市场中，CDS 和 bond 的流动性不一样，在国外 CDS 流动性大，在国内由于 CDS 是新生事物市场深度不够，bond 流动性大。因此 CDS 和 bond 的信用价差会不一样，用 bond-CDS basis (基差) 来定义它

    bond-CDS basis = s_CDS - s_bond

套利者根据基差的正负来套利。

• 假如基差为负，s_CDS 小于 s_bond，做多 bond 并当 CDS 的保护买方，从 CDS 支付低的 s_CDS 来领取高的 s_bond。

• 假如基差为正，s_CDS 大于 s_bond，做空 bond 并当 CDS 的保护卖方，从 CDS 领取高的 s_CDS 来支付低的 s_bond。

下节我们用 CDS 信用价差举例。

4.2

真实操作

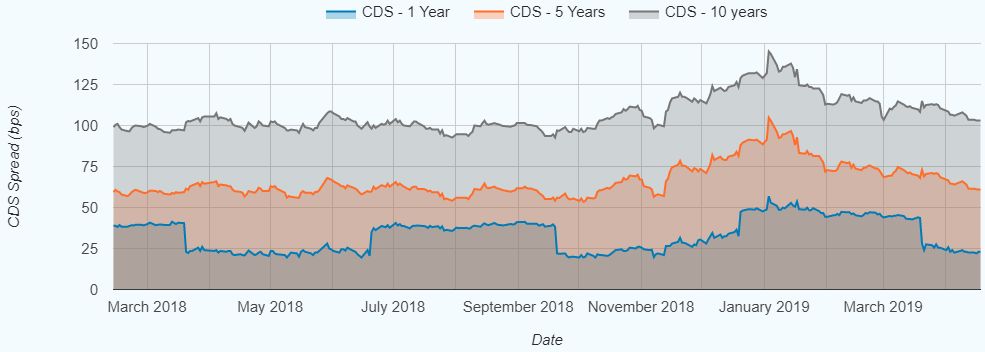
市场上的 CDS 信用价差报价通常涉及 3 个标准期限 - 1Y、5Y 和 10Y。下图是摩根斯坦利一年里每天的 CDS 信用价差。

从 CDS 信用价差可以用 bootstrapping 的方法推出危险率 (hazard rate) 和违约概率 (probability of default) 等信息。

理论上，危险率是一个违约的条件概率。在一个极短的时间段 ∆t，在 t 时刻危险率 λ_t 的定义为：违约发生在 t 到 t+∆t 的条件概率，给定 t 时刻前未发生任何违约事件。

若 Q(t) 为在 t 时刻的存活概率 (t 时刻前未发生任何违约事件)，那么根据定义，

取极限 ∆t → 0，解下列微分方程

有了 1Y、5Y 和 10Y 三个 CDS 信用价差的报价，我们可以建立三个 CDS的现值方程，再假设 λ_t 是分段常数，可以解出 λ_0-1, λ_1-5, λ_5-10 三个危险率值，也可以解出任何点上的存活概率和违约概率。

5

波动率

5.1

直观理解

波动率 (volatility) 是描述价格在一段时间内的变化程度，这个价格可以是利率、汇率和其他金融资产的价格。

波动率是对资产收益率不确定性的衡量，因此用于反映金融资产的风险水平。

• 波动率越高，金融资产价格的波动越剧烈，资产收益率的不确定性就越强

• 波动率越低，金融资产价格的波动越平缓，资产收益率的确定性就越强

波动率可以分成三类，实际波动率只是一个概念，历史波动率从原生资产的时间序列中计算，隐含波动率从衍生品 (期权) 的公式和交易价格反推。

• 实际波动率：实际波动率又称作未来波动率，它永远是一个未知数，或者只是个概念

• 历史波动率：历史波动率是指投资回报率在过去一段时间内所表现出的波动率，它由标的资产市场价格过去一段时间的历史数据反映。历史波动率是往后看 (backward looking) 的。

• 隐含波动率：隐含波动率是通过市场交易的期权价格，和 Black-Scholes 公式反解出来的原生资产的波动率。隐含波动率是往前看 (forward looking) 的，可看成为市场实际波动率的预期。

5.2

真实操作

历史波动率计算加来很简单，只要根据价格求出收益，然后求出其标准差即可。本节我们关注的是隐含波动率，只要一个原生资产有衍生品在市场上交易，我们都应该用其隐含波动率来校正模型或者来估值其他更复杂的产品。

已知市场价格 V 和 BS 公式形式，反推隐含波动率 σ。 

    BS(S, K, T, r, b, σ) = V

=>

    σ = BS-1(V, S, K, T, r, b)

    

其中 BS-1 是它的反函数，没有解析解，通常用数值解来求 σ。

对利率、外汇、股票、商品和信用期权，市场在标准期限和标准行权价格 (标准价内水平) 都有隐含波动率的报价 (除非没有成交量)。因此不需要我们自己计算。

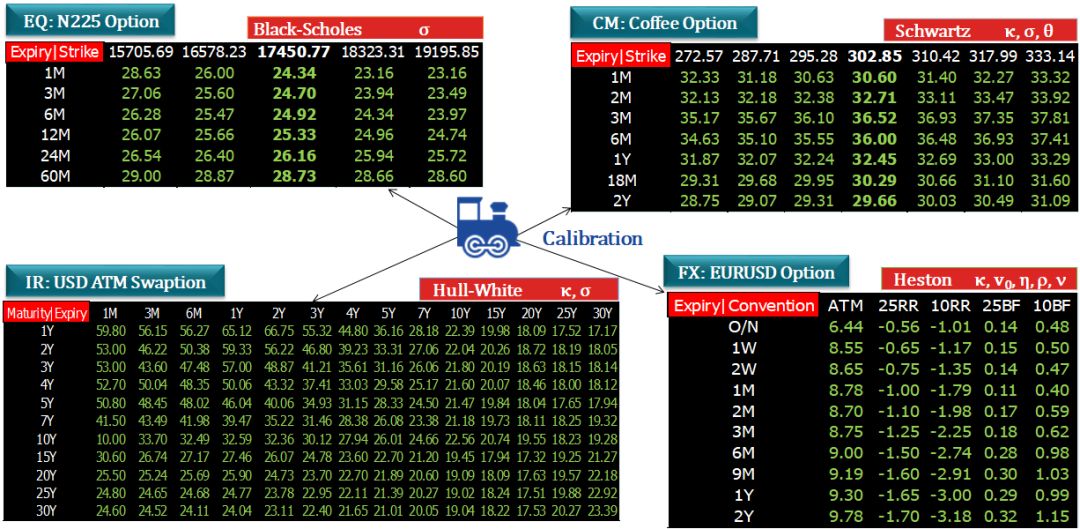
下图给出市场报价的利率、外汇、股票、商品隐含波动率平面。

6

插值

前面五节给出各种市场变量的算法以及相对应的市场报价 (有限的标准点上)，但是在对金融产品进行估值时，我们需要在无限的非标准点的市场变量的值，怎么办？用插值！

具体例子

下面我们来看两个例子是如何生成零息债价格和波动率的。

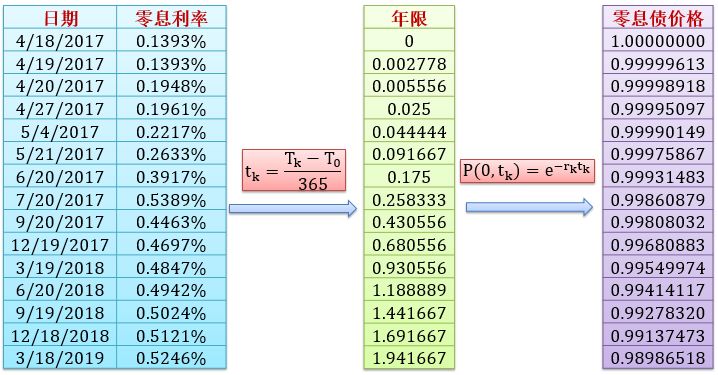
零息债价格

 

从期限维度上进行线性内插 (linear interpolation) 来获取零息债价格

波动率

从期权期限和执行价格两个维度上进行线性内插 (linear interpolation) 及平外插 (flat extrapolation) 来获取波动率

插值方式

上面例子都是用分段线性函数插值，实际上常用的还有分段常函数、分段三次条函数等等。

给定 N 数据点 (x_i, f_i), i = 1, 2, …, N，其中 x₁ < x₂ < ... < x_N 。我们希望找到一个函数 f(x) 来拟合这 N 个数据点，对于分段函数，因为有 N 个数据点，需要 N -1 段函数。

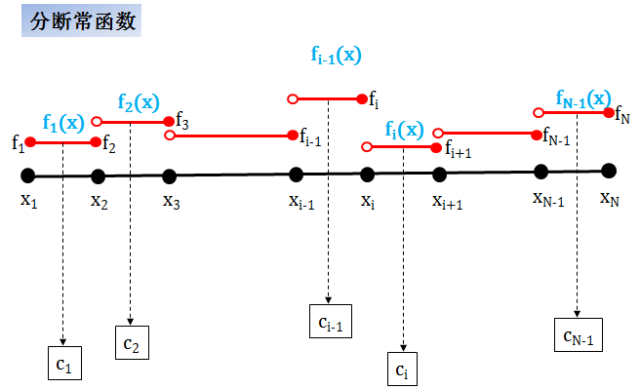
分段常 (piecewise constant) 函数

在这种情况，每一段函数都是一个常数，这种插值方法

 

• 优点是简单

• 缺点是在数据点上不连续，更不可导

• 适用于在某些模型的参数 (比如 Heston 模型中的均值回归率和波动率的波动率) 上插值 (模型参数通常只用常数和分段常函数，但后者比前者能更好的拟合市场数据，因为它有更多自由度)。

• 不适用于曲线和波动率插值

分段常函数不连续，通常称作 C^-1 函数。

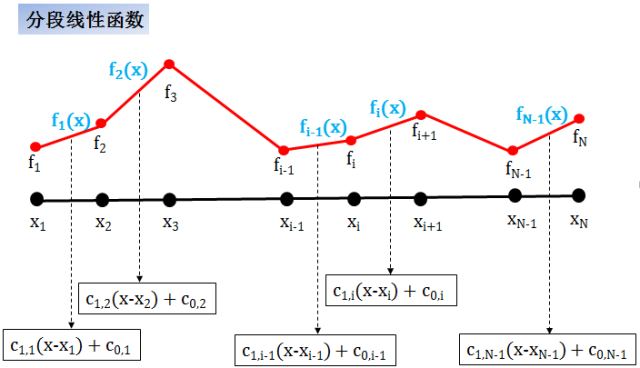
分段线性 (piecewise linear) 函数

在这种情况，每一段函数都是一个线性函数，这种插值方法

• 优点是简单，在数据点上连续，而且形状保持性很好 (插出的值只和它相邻两个数据点有关，别的数据怎么动都不影响它的插值)

• 缺点是在数据点上不可导

• 适用于曲线和波动率插值

• 不适用于在 Hull-White 模型下的曲线插值 (Hull-White 模型需要对曲线求二阶导)

分段线性函数连续但是不可导，通常称作 C⁰ 函数。

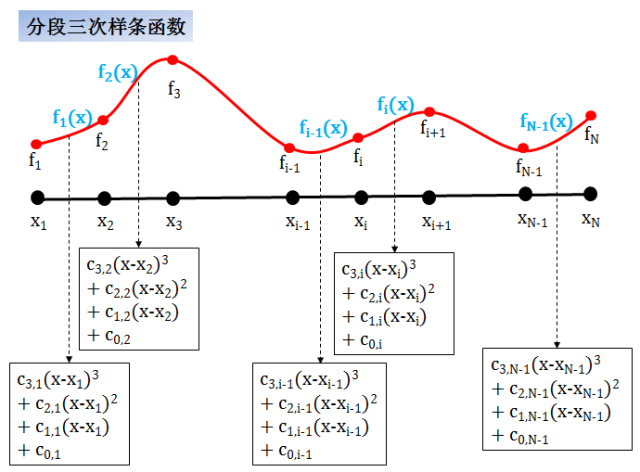
分段三次样条 (piecewise cubic spline) 函数

在这种情况，每一段函数都是一个三次多项式函数，这种插值方法

• 优点是在数据点上可导甚至可导三次 (非常平滑)

• 缺点是有些复杂，而且形状保持性不好 (插出的值和整个数据点有关，别的数据动以下都会影响它的插值)

• 适用于曲线的插值

分段三次样条函数连续而且二阶可导，通常称作 C² 函数。

---

讲到这里细心的同学可能会发现，怎么没有连续而且一阶可导的 C¹ 函数？有的，它是分段埃尔米特 (piecewise Hermite) 函数。它和三次样条函数一样，每段都是一个三次多项式函数，但是在节点( 数据点)上的连接导数设置有所不同，埃尔米特函数就只处理了一阶导数。

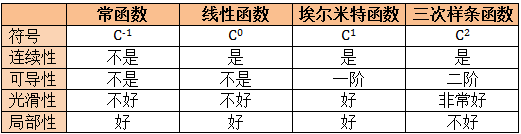
从分段常函数到分段线性函到分段三次样条函数，内插出来的值化成函数看起来越来越光滑 (可导性越来越好)，但是形状保持性越来越差 (局部性越来越差)。当我们选择那种方法插值时，我们需要权衡插出曲线的局部性 (locality) 和可导性 (differentiability)。

下表总结四种内插函数

7

总结

了解各种市场变量的计算方法，以及插出非标准点的变量对于之后的曲线构建、模型校正、产品估值、风险计量都至关重要。

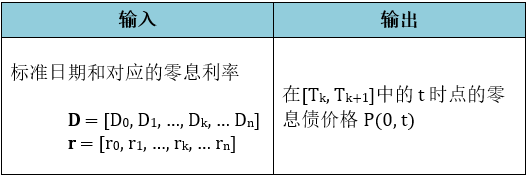
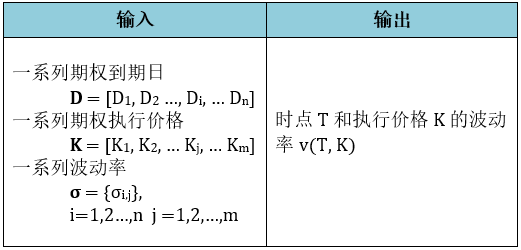
在变量计算这一模块，我们可以设计成一个获取函数 (Extraction function)，

• 输入是任意非标准点

• 输出是该点对应的变量

获取函数就是内插函数 (interpolation) 和外插函数 (extrapolation)。核心理念就是从市场已有的标准点对应的变量内插或外插出非标准点对应的变量。

在实操中，我们会评估不同插值方法的优劣，甚至在什么变量上插值，两个例子：

1. 利率曲线：在对数折现因子上线性插值和在瞬时远期利率上平插是一样的，它们可以大概率的保证没有负的远期利率出现。

   
   

2. 外汇波动率曲线 delta 维度：在 log(moneyness) 上插值而不是在 delta 上插值。

   
   

3. 波动率曲线时间维度：在方差上插值而不是在波动率上插值，前者可以保证远期波动率为正。

   
   

4. CDS 危险率曲线：在远期危险率上做平插，可以使得保护端的有解析解，要不然只有数值解。

在外汇市场，实证分析证明在周末时的波动率没有非周末时的波动率大，如何处理这种情况？给周末和非周末加权重，比如非周末放 1 周末放 0.2。

内插和外插不仅仅只局限于简单函数，还有可能是复杂模型，比如 Vanna-Volga 或 SABR。

这些更为细节的东西就以后写在书里面吧。hiahia

Stay Tuned！

王的机器

机器学习、金融工程、量化投资的干货营；快乐硬核的终生学习者。