最长公共子串求解套路

作者 | 码海

出品 | 码海（ID:seaofcode）

头图 |  CSDN 下载自东方IC

前言

动态规划是大厂的热门考点，其中最长公共子串与最长公共子序列这两道题出现得尤其频繁，这两道题其实有挺多变种，很适合考察侯选人对动态规划的掌握情况，今天我们就先来看看如何求解最长公共子串，图文并茂，清晰易懂！

最长公共子串

题目如下：

输入:  x = ["", "a", "b", "c", "a", "d", "f"]
       y = ["", "a", "c", "b", "a", "d"],

输出: 2
解释: 最长公共子串为 ad，所以结果为 2

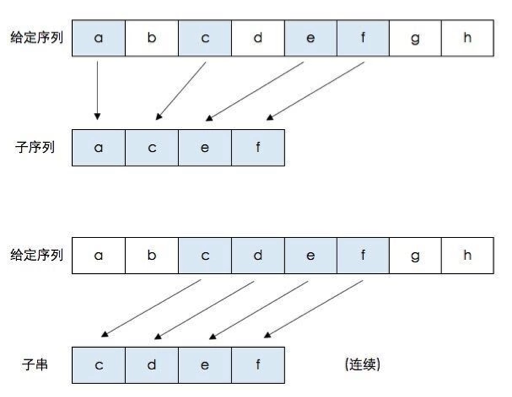
这里需要简单解释下子串与子序列的区别，子串要求这串字符串在原字符串中是连续的，而子序列可以不连续，两者的区别如下：

如果不清楚啥是动态规划的同学，强烈建议先学习下此文，其对动态规划的分析，解题套路中有详细的阐述，好评如潮!对理解动态规划有很大的帮助。

首先看下，如果这题如果用暴力求解的话，应该算出每个字符串的所有子字符串，然后再对所有子字符串进行比较，是个排列组合问题，时间复杂度很大，不可取！所以我们看下怎么用动态规划来解。

解动态规划需要至少明确以下三个概念

• base case
• 状态转移方程
• 自下而上

动态规划一言以蔽之就是利用 「base case 」和「状态转移方程」然后「自下而上」得求得最终问题的解。相对递归的自上而下求解造成的大量子问题的计算，自下而上意味着每个子问题不会被重复计算，很好地达到了「剪枝」的效果。这其中「状态转移方程」的求解无疑是重要的，如果求得了「状态转移」方程，问题其实就解决地差不多了。

回到最长公共子串本身来看，我们来看看它的「状态转移方程」和「base case」是啥。

1、状态转移方程

这题的状态转移方程该怎么定义呢，首先我们求的是两个字符串的公共子串，所以应该意识到这个 dp 方程是个二维数组 dp[i][j]，代表的 x 的前 i 个字符串与 y 的 前 j 个字符串的最长公共子串,那么状态状态方程该怎么得出来呢，一般对于字符串类的动态规划来说，我们可以利用「状态转移表」法来帮助我们得出状态转移方程

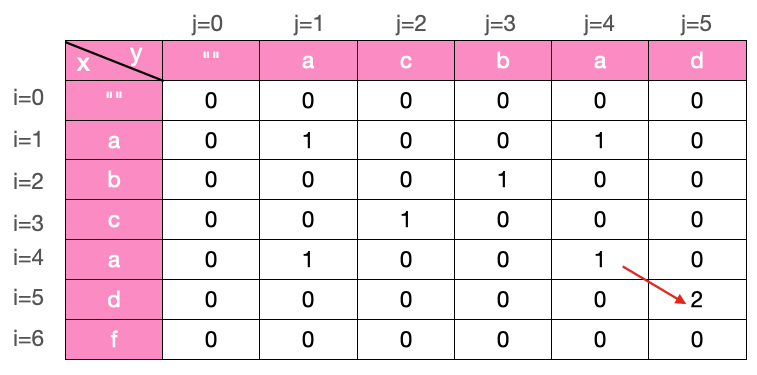
观察出规律了吗，对于 dp[i][j] 来说，它的值有两种可能，取决于字符 x[i] 和 y[j] 这两个字符是否相等

如果两个字符相等，则 dp[i][j] = dp[i-1][j-1] + 1（注意图中的箭头）, 怎么理解，1 代表 x 的第 i 个字符与 y 的第 j 个字符相等，根据 dp[i][j] 的定义，那么它自然等于  x 的前 i-1 个字符串与 y 的 前 j-1 个字符串的最长公共子串 + 1，如下图示

如果 x 的第 i 个字符与 y 的第 j 个字符不相等， 那么显然 dp[i][j] = 0，因为 dp[i][j] 定义为最长公共子串，所以只要有一个字符不相等，就说明不满足最长公共子串这个定义，自然 dp[i][j] 为 0 了。

根据以上条件可知状态转移方程为

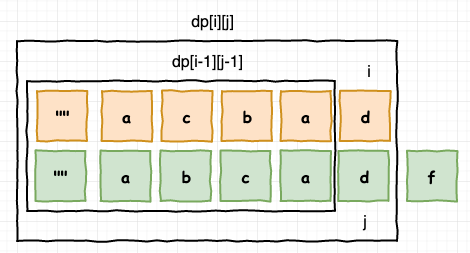
2、base case

显然图中黄色格子所示为 base case

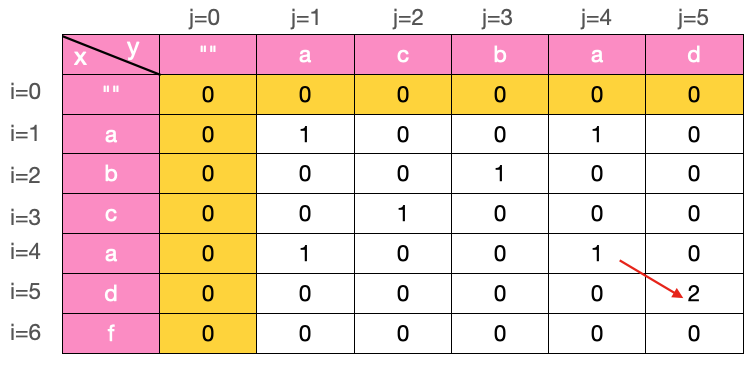
即可用如下公式表示

这也比较好理解，dp[0][i] 或 dp[j][0] 即空字符串与任意字符串的最大公共子串显然为0。

3、求解

有了状态转移方程，有了 base case, 求解不是难事，需要注意的是最长公共子串长度并不是右下角方格子的数字（dp[5][6]）,而是 dp[5][5]，这与一般的动态规划解题套路有些不同，我们可以用一个临时变量来表示最长公共子串。

代码如下：

public class Solution {    public static int getLCS(char[] x, char[] y) {        // base case，默认 dp 中的每个元素都为 0。        int dp[][] = new int[x.length][y.length];                // 最长公共子串， 用一个临时变量表示        int resultLCS = 0;        for (int i = 1; i < x.length; i++) {            for (int j = 1; j < y.length; j++) {                // 以下是状态转移方程                if (x[i] == y[j]) {                    dp[i][j] = dp[i-1][j-1] + 1;                    resultLCS = Math.max(resultLCS, dp[i][j]);                } else {                    dp[i][j] = 0;                }            }        }        return resultLCS;    }
    public static void main(String[] args) {        char[] x =  {' ', 'a', 'c', 'b', 'a', 'd'};        char[] y =  {' ', 'a', 'b', 'c', 'a', 'd', 'f'};        int lcs = Solution.getLCS(x, y);        System.out.println("lcs = " + lcs);    }}

求解完成，但别忘了分析时间和空间复杂度，看下是否有优化的空间，这两点是很多同学做算法题常见遗漏的地方。

先来看下时间复杂度，两重循环，所以时间复杂度显然为 O(n^2)。空间复杂度呢，二维数组，所以是 O(n^2)，时间复杂度没法优化了，那么空间复杂度呢，其实可以优化为 O(n), 怎么优化，这里就要提一下动态规划的「无后效性」了。

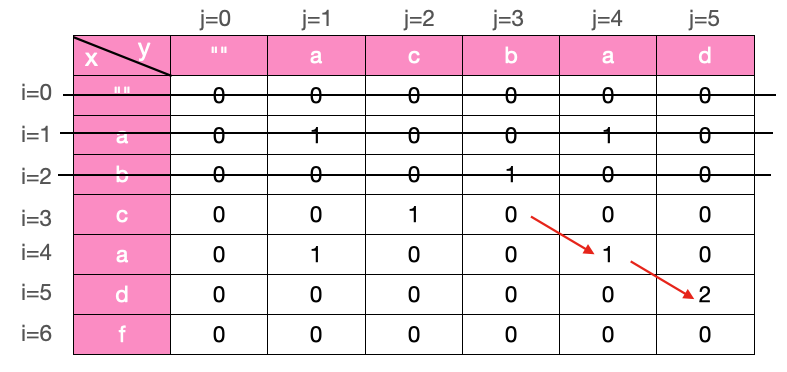
对于各个格子中的数字，它只与其上一行的左上角格子数字有关，与上一行之前的行无关（所以在计算 i = 4 行的格子中，图中 0，1，2 行的格子无需保留），这叫无后效性。

上图中 i=4, j=4 对应的格子中的数字 1 只与其左上角的格子数字 0 有关，所以我们要有一个数组记录其上一行的数字，另外 1 所在行的格子中的数字也要记下来，因为它下一行中格子的数字也是基于本行（1 所在行）的数字推导而来，比如 2 就是基于 1 推导而来的。

由此分析我们要有两个一维数组保留两行的数据，这里的两个数组其实是滚动数组，啥意思呢，我简单解释一下

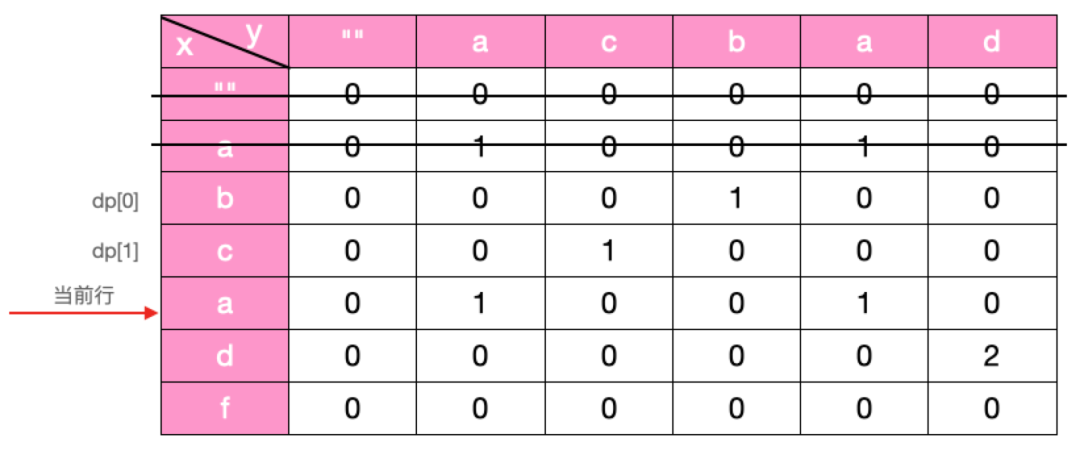
比如当要计算箭头所指行中格子的数字时，显然，它只与 dp[1] 中格子的数字有关，而与 dp[0] 所指行无关，所以当前行格子的计算结果可以根据 dp[1] 计算出结果放在 dp[0] 中，计算后如下：

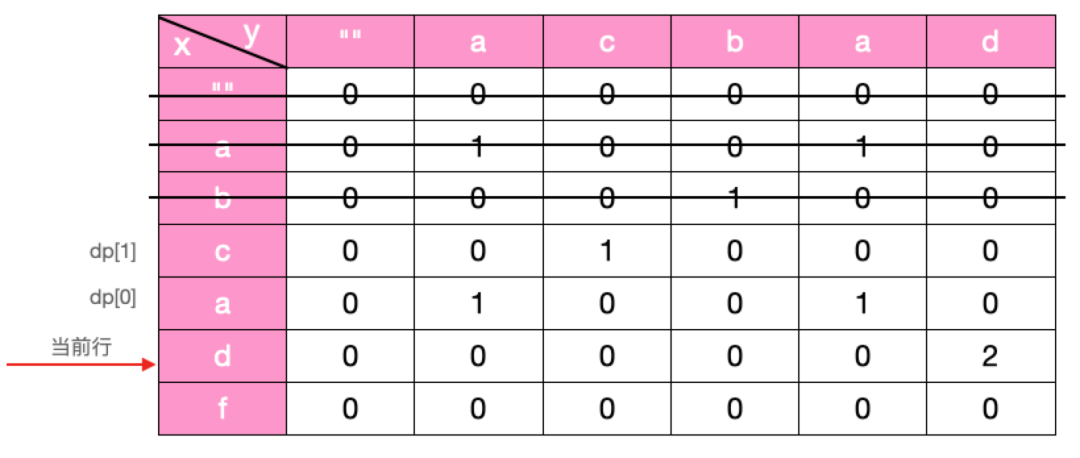
现在要计算当前行的格子数，它只与 dp[0] 有关，而与 dp[1] 无关，所以当前行的格子数字可以根据 dp[0] 计算出结果保存在 dp[1] 中。到底是取 dp[0] 还是 dp[1] 呢，这里有一个巧妙的方法：将「当前行&1」的结果与 1 进行比较，比如相等，也就是当前行数为奇数时，则它的结果依赖于 dp[0]，当前行的结果写入 dp[1] 中，如果不相等，也就是当前行为偶数时，则它的结果依赖于 dp[1]，当前行的结果写入 dp[0] 。

优化后的代码如下。

public class Solution {    public static int getLCS(char[] x, char[] y) {        // base case，使用滚动数组进行优化        int dp[][] = new int[2][y.length];
        // 最长公共子串， 用一个临时变量表示        int resultLCS = 0;        for (int i = 1; i < x.length; i++) {            for (int j = 1; j < y.length; j++) {                // 滚动数组                int cur = (i & 1) == 1 ? 1 : 0;                int pre = (i & 1) == 0 ? 1 : 0;
                // 状态转移方程                if (x[i] == y[j]) {                    dp[cur][j] = dp[pre][j-1] + 1;                    resultLCS = Math.max(resultLCS, dp[cur][j]);                } else {                    dp[cur][j] = 0;                }            }        }        return resultLCS;    }
    public static void main(String[] args) {        char[] x =  {' ', 'a', 'b', 'c', 'a', 'd', 'f'};        char[] y =  {' ', 'a', 'c', 'b', 'a', 'd'};        int lcs = Solution.getLCS(x, y);        System.out.println("lcs = " + lcs);    }}

这样的话我们就将空间复杂度优化成了 O(n)。需要说明的事，利用动态规划的无后效性，通常都可以将空间进行压缩，将空间复杂度降低一个层级，所以大家在做完动态规划的算法题后，还是可以再进一步考虑下问题的复杂度是否还可以继续优化。

4、问题变形

以上我们只是简单求了一下最长公共子串的长度，那如何求其对应的子串呢。还是根据状态状态转移来求，但我们要额外加两个变量 max_row, max_column 代表最长公共子串长度对应的格子的坐标。这样根据状态转移方程可以依次反求得其格子对应的字符，如图示:

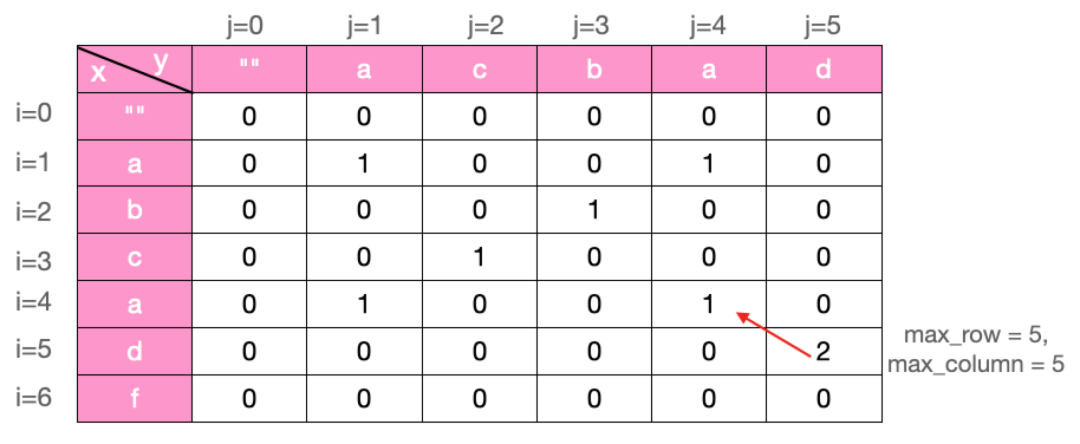
代码如下：

public class Solution {    public static void printLCS(char[] x, char[] y) {        // base case，默认 dp 中的每个元素都为 0。        int dp[][] = new int[x.length][y.length];
        // 最长公共子串， 用一个临时变量表示        int resultLCS = 0;
        // 记录最长公共子串对应的最后一个格子的模坐标,纵坐标也可以        int maxRow = 0, maxColumn = 0;        for (int i = 1; i < x.length; i++) {            for (int j = 1; j < y.length; j++) {                // 以下是状态转移方程                if (x[i] == y[j]) {                    dp[i][j] = dp[i-1][j-1] + 1;                    if (dp[i][j] >= resultLCS) {                        resultLCS = dp[i][j];                        maxRow = i;                        maxColumn = j;                    }                } else {                    dp[i][j] = 0;                }            }        }
        List<Integer> result = new ArrayList<>();        // 根据状态转移方程反推最长公共子序列        while (dp[maxRow][maxColumn] > 0) {            result.add(Integer.valueOf(x[maxRow]));            maxRow = maxRow-1;            maxColumn = maxColumn-1;        }
        // 算出的最长公共子序列为逆序的，需要反转一下        Collections.reverse(result);
        for (Integer item : result) {            System.out.print((char) item.intValue());        }    }
    public static void main(String[] args) {        char[] x =  {' ', 'a', 'c', 'b', 'a', 'd'};        char[] y =  {' ', 'a', 'b', 'c', 'a', 'd', 'f'};        Solution.printLCS(x, y);    }}

总结

本文用图文并茂的方式讲述了动态规划的解题套路，相信大家对字符串类型的动态规划解题技巧应该有了进一步的理解，首先最重要的一步当然是明确 dp 的定义，其实字符串类的动态规划问题一般可以用状态转移表法来观察状态转移方程，得出了状态转移方程，思路也就厘清得八九不离十了，另外当解决完之后，最好思考一下时间/空间复杂度是否有优化的空间，一般可以根据动态规划的无后效性来进一步优化复杂度，通过这样不断地优化自然可以得出问题的最优解。

更多精彩推荐
☞JavaScript 爆红后，微软为何还要开发 TypeScript？
☞打通语言理论和统计 NLP 两个世界，Transformers/GNNs 架构能做到吗？
☞2020互联网公司中秋礼盒大比拼！（文末送福利）
☞自拍卡通化，拯救动画师，StyleGAN再次玩出新花样
☞还不懂Redis？看完这个故事就明白了！
☞区块链+生鲜：杜绝“偷梁换柱”和“以次充好”

点分享
点点赞
点在看