机器学习中有哪些形式简单却很巧妙的idea?
加入极市专业CV交流群,与6000+来自腾讯,华为,百度,北大,清华,中科院等名企名校视觉开发者互动交流!更有机会与李开复老师等大牛群内互动!
同时提供每月大咖直播分享、真实项目需求对接、干货资讯汇总,行业技术交流。关注 极市平台 公众号 ,回复 加群,立刻申请入群~
致歉:
12月11日晚由于小编的操作失误,造成文章内容出现错误,因此删除文章进行了重新发布,对您造成的不便我们感到非常抱歉。
问题:机器学习中有哪些形式简单却很巧妙的idea?
AI论文中,有哪些像GAN这种形式简单却功能强大的idea。
https://www.zhihu.com/question/347847220
知乎高质量回答
本文来自知乎问答,回答已获作者授权,禁止二次转载
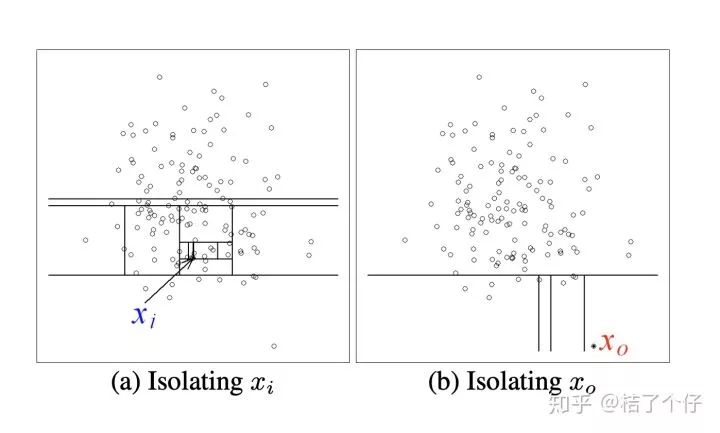
异常检查算法Isolation Forest(孤立森林)
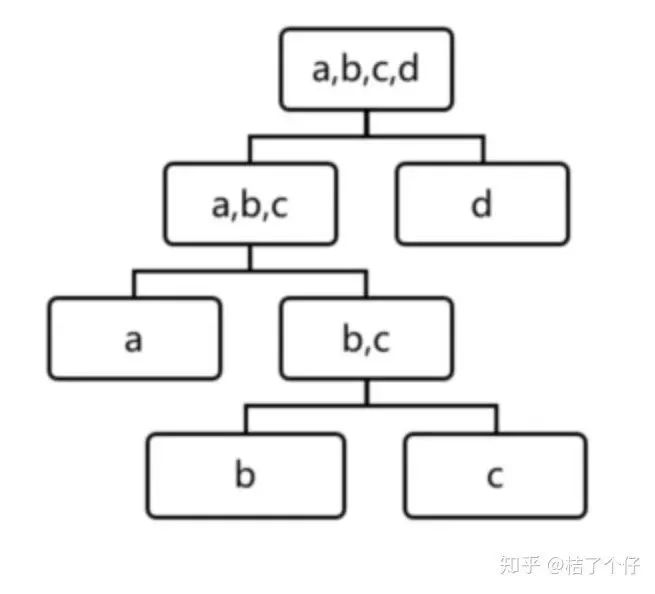
为了更直观,有更多一步了解,请看下图,直觉上我们就知道xi是普通点, x0是异常点。那么用Isolation tree怎么解释呢?
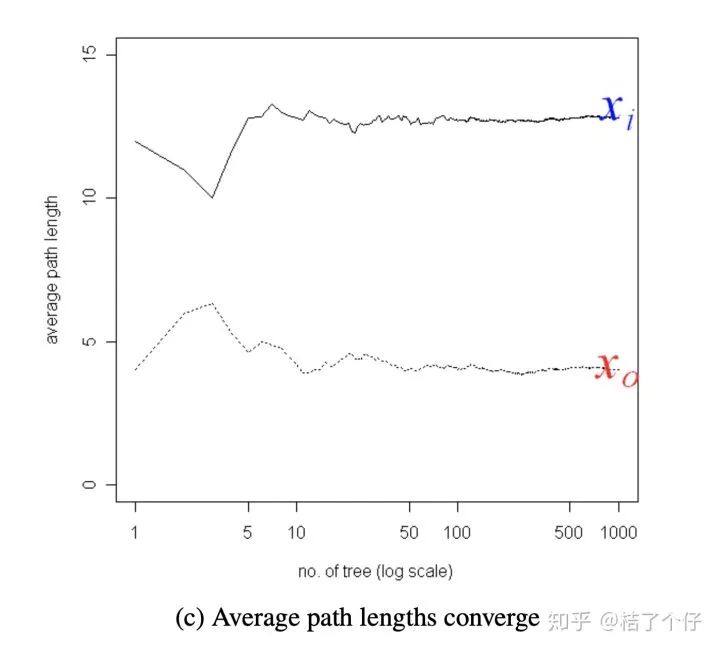
本文来自知乎问答,仅供学习参考使用,著作权归作者所有
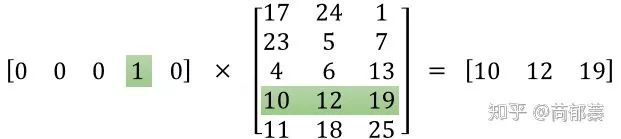
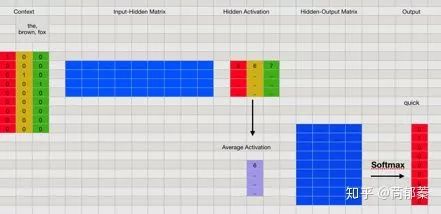

本文来自知乎问答, 仅供学习参考使用,著作权归作者所有
Online learning
-
Flaxman et al. 的gradient descent without a gradient里的one-point estimator,可以在没有梯度的情况下做在线梯度下降(bandit convex optimization最早的文章之一)。 -
Adversarial bandit里面的 importance-weighted estimator。 -
Bubeck et al.的Bandit Convex Optimization: \sqrt{T} Regret in One Dimension里引入prior进行线性化,然后用minimax theorem对inf和sup进行换序,可以非构造性地计算minimax regret的界。
Optimization
-
Lezcano-Casado and Mart´ınez-Rubio的ICML'19的文章Cheap Orthogonal Constraints in Neural Networks: A Simple Parametrization of the Orthogonal and Unitary Group: 比如一个优化问题的变量是一个矩阵,约束是要求它是 SO(n)的,这篇文章用exponential map把它变成一个在skew symmetric 矩阵上的可以说是无约束的优化问题。
Submodular optimization
-
Vondrak的Symmetry and approximability of submodular maximization problems里的symmetry gap: submodular优化的难度和问题的对称性有关。
四、作者:及时物语
https://www.zhihu.com/question/347847220/answer/844085093
本文来自知乎问答,仅供学习参考使用,著作权归作者所有
近邻成分分析NCA:
https://mp.weixin.qq.com/s/LGazJxEFWVxUF2KudY5PTA
近邻成分分析(Neighborhood Component Analysis,NCA)是一种非参数的特征选择方法,属于监督学习,其目标是使回归和分类算法的预测精度最大化,但在这个过程的同时,达到降维的目的。即,NCA的降维是和回归和分类的过程交织在一起的。
一、NCA既可以用于分类,又可以用于回归。这里主要讲一下分类算法中的NCA。
我们先从一个简单的随机多类分类器着手,过程及其简单,如下:
1.在数据集中随机选取一个点,我们叫它Ref(x),将它作为点x(点x就是我们需要预测的未知类别的点)的“参考点”。
2.用Ref(x)的类别标签来标注x。
咋样,是不是很简单,也很蠢的方法?因为分类好像完全是随机的。现在我们透过表面看实质,我们发现这个方案有点类似于1-NN分类器(K=1时候的KNN),在1-NN中,“参考点”会选择离x最近的点。而在NCA中,“参考点”是随机选择的,训练集中所有的点都有一定概率被选为参考点。当然,不是完全的随机,当训练集的点xj离x越近时,被选中的几率就会越大,其距离函数dw为
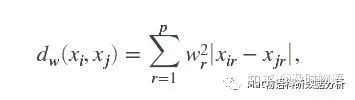
其中wr是“特征权重”,根据上面的思路,我们假设
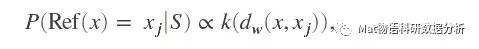
即P正比于k(dw),其中k是某种相似度函数,只需要满足dw越小,k就越大就行,比如
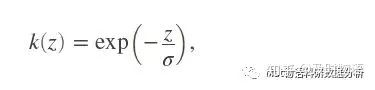
就是一个很好的选择。为了让所有的P之和正好等于1,让
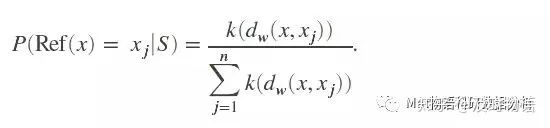
OK,一个分类器就设计好了,简直比KNN还科学,等等,喂,特征选择在哪里?
确实,以上的分类器已经可以用了,但想达到特征选择的目的,还需要对模型进行训练,这里采用“留一”的策略,并将结合正则化方法。
我们用去掉了xi的集s-i来预测xi的类别,那么,xj(xj不等于xi)被选为参考点的概率应该为:
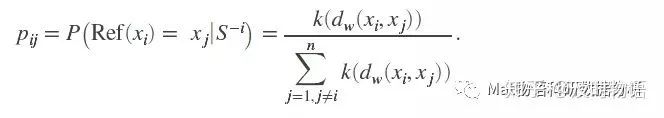
对于xi,把所有的s-i的点都算一遍,那么这个“留一”法的平均正确率pi为
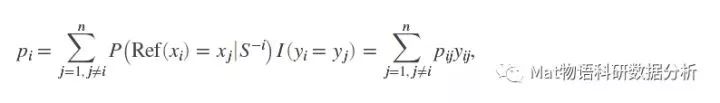
其中当yi=yj时,yij=1,否则等于0。
那么对于整个分类的平均留一正确率:
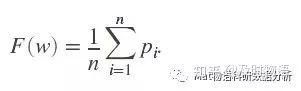
以看出,fw式子右边依赖于权重向量w。那么关键来了。NCA的目标即调整w,使fw最大化。这里我们使用正则化的目标函数:
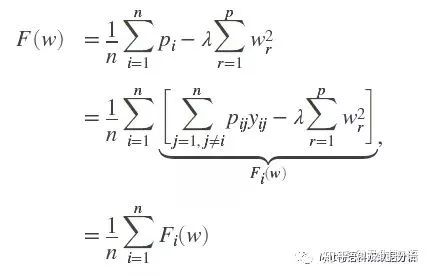
其中λ为正则化参数,会使得许多w中的权重变为0.
这里简直和L2正则化的岭回归像极了,也可以看出L2正则化对于w权重衰减为0的作用(对于w衰减的效果和岭回归异曲同工)。后面就仅仅是优化的步骤了,具体步骤这里暂时不写,只列出公式如下。
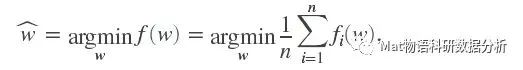
二、对于NCA回归,则和NCA分类基本原理相同,用li来度量y之间的距离,公式稍有变化:
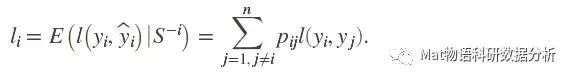
最后的目标函数如下,以l代替分类中的p:
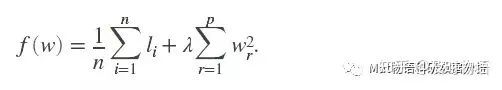
三、两个小小的注意事项
1.数据标准化的影响
在NCA中,所有的权重只有一个参数λ,因此要求权重的大小可以互相比较,而当xi的特征尺度相差过大时候,“权重比较”失去意义,因此,和以往一样,当特征尺度产局过大时,需要进行标准化。
2.如何选择正则化参数λ
通常,我们选择不同数量级的λ,在同一个训练集上计算NCA的性能。(直白地说,就是并没有什么好的方法)
NCA是一种较新的技术,由Jacob Goldberger,Sam Roweis,Ruslan Salakhudinov和Geoff Hinton等人于2004年在多伦多大学计算机系创建,近年来才渐渐开始被应用。相比其它传统的特征选择方法,其能同时应用在分类和回归两种问题中,并能在更复杂的系统(如80%干扰特征及诸多离群值数据)中,准确识别出真正有价值的特征。
五、作者:Evan
https://www.zhihu.com/question/347847220/answer/871450361
本文来自知乎问答,仅供学习参考使用,著作权归作者所有
私以为越是基础的方法越是巧妙!!!
比如机器学习和统计里面大家都熟知的数据降维方法主成分分析(Principal components analysis,PCA)。我们都知道很多数据来源如果表示成向量 都非常的高维(比如语音信号、图像信号),而统计分析或者批量地可视化这种高维数据在数学上是比较困难的。
为了解决这种困难,早起(雾,早期)的数学家和统计学家们决定降低它们的维度,通过一种线性变换的方式 。假定 ,那么一般要求 远大于 。PCA的关键就在于如何获取一个合理的矩阵 ,而“合理”的核心其实是我们希望得到什么样的低维数据表达。
一、PCA的一个出发点是希望投影后的数据 在每一维上都能有比较大的散度(也可以理解成方差)。这个思路其实非常的intuitive,设想如果数据给了很多数据在某一维上的值都没什么差别,大概率这一维对后续的任务(比如分类、回归)也没什么帮助。
以 的情况为例,这时候我们可以把 写成 方便理解,如果给定了 个样本 ,我们的目标其实可以写成一个优化问题:
(注意方便起见这里假设 )
如果引入一个数据矩阵 ,那么这个优化问题又可以简单写成:
有一定矩阵基础的小伙伴这个时候应该知道最优解就是 的第一个特征向量了。偏好数值分析的小伙伴也可以通过引入Lagrange乘子得到同样的结论,具体参照PRML。
二、PCA的另一个经典视角比较几何。其实数据降维可以考虑成从欧式空间到嵌入流型的投影(参考三位空间中将一些点向同一个平面进行投影的例子)。我们当然希望投影之后的点的位置距离他们原始的位置比较近。
那么从这个角度出发,我们又有这样一个优化问题 (这里矩阵 的每一行都是一个单位矢量)进而可以得到同样的基于特征分解的formulation。是不是一颗赛艇?
-End-
CV细分方向交流群
添加极市小助手微信(ID : cv-mart),备注:研究方向-姓名-学校/公司-城市(如:目标检测-小极-北大-深圳),即可申请加入目标检测、目标跟踪、人脸、工业检测、医学影像、三维&SLAM、图像分割、姿态估计、超分辨率、嵌入式视觉、OCR 等极市技术交流群(已经添加小助手的好友直接私信),更有每月大咖直播分享、真实项目需求对接、干货资讯汇总,行业技术交流,一起来让思想之光照的更远吧~
△长按添加极市小助手
△长按关注极市平台
觉得有用麻烦给个在看啦~