清华小哥用 Python 实现主成分分析

在数据分析的过程中，我们会通过观察一系列的特征属性来对我们感兴趣的对象进行分析研究，一方面特征属性越多，越有利于我们细致刻画事物，但另一方面也会增加后续数据处理的运算量，带来较大的处理负担，我们应该如何平衡好这个问题？利用矩阵的特征值分解进行主成分分析就是一个很好的解决途径。

主成分分析是机器学习中的核心算法之一，本文将基于 Python 语言，为读者深入浅出的分析他的来龙去脉和本质内涵，相信读完此文，将扫清你心中的所有疑虑，今后在应用他解决实际问题的时候也能更加得心应手。

本文主要内容有

• 对称矩阵的基本性质

• 对称矩阵的对角化与特征值

• 数据降维的需求背景与主要目标

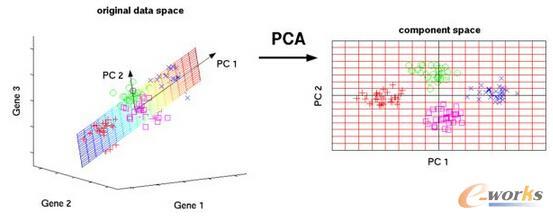
• 主成分分析法降维的核心思路

• 主成分分析的细节实现过程

• 推广到 N 个特征的降维实现

作者

张雨萌，清华大学计算机科学与技术系硕士毕业，研究方向：数据分析、自然语言处理；知乎科技专栏作家，专栏关注量15000；个人已出版机器学习算法类技术书籍。

下文是文章的一段截取内容。

期望与方差

看到这个标题，读者也许会想，这里不是在讲线性代数么，怎么感觉像是误入了概率统计的课堂？

这里我专门说明一下，在这一节里，我们的最终目标是分析如何提取数据的主成分，如何对手头的数据进行降维，以便后续的进一步分析。往往问题的切入点就是数据各个维度之间的关系以及数据的整体分布。因此，我们有必要花上一点功夫，来梳理一下如何对数据的整体分布情况进行描述。

首先大家知道，期望衡量的是一组变量 X 取值分布的平均值，我们一般记作：E[X]，反映的是不同数据集的整体水平。比如，在一次期末考试中，一班的平均成绩是 90 分，二班的平均成绩是 85 分，那么从这两个班级成绩的均值来看，就反映出一班的成绩在总体上要优于二班。

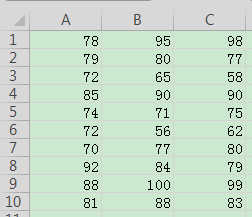
这里有一组数据，他描述了10名同学的考试成绩，第一列是英语成绩，第二列是数学成绩，第三列是物理成绩，我们将数据文件保存在E盘上，数据文件的截图如图1所示：

我们来求解一下这三门成绩的均值和方差。

代码片段：

import numpy as np

eng,mat,phy=np.loadtxt('e:\\score.csv',delimiter=',',usecols=(0, 1, 2), unpack=True)

print(eng.mean(), mat.mean(), phy.mean())
print(np.cov(eng), np.cov(mat), np.cov(phy))

运行结果：

79.1 80.6 80.1
54.98888888888888 188.04444444444442 181.87777777777777

从运行结果中我们可以看出这10名同学的英语、数学、物理三门功课的成绩所体现出的一些特征。三门课的平均值都差不多，但是方差值相差非常大，英语成绩的方差要明显小于数学和物理成绩的方差，这恰恰说明了这10名同学的英语成绩的分布相对而言要集中一些，换句话说就是大家的成绩相差不大，而另外两门理科的分数分布的则要更加分散，成绩差距相对更大。

如果你对这篇文章感兴趣，直接扫描下方二维码就能立刻阅读，还能和一群技术人进去交流分享。

        或者点击“阅读原文”，也可以立刻阅读哦～