学界 | 神经网络碰上高斯过程，DeepMind连发两篇论文开启深度学习新方向

选自arXiv

机器之心编译

参与：思源、晓坤

神经网络目前是最强大的函数近似器，而高斯过程是另一种非常强大的近似方法。DeepMind 刚刚提出了两篇结合高斯过程与神经网络的研究，这种模型能获得神经网络训练上的高效性，与高斯过程在推断时的灵活性。DeepMind 分别称这两种模型为神经过程与条件神经过程，它们通过神经网络学习逼近随机过程，并能处理监督学习问题。

函数近似是机器学习众多问题的核心，而过去深度神经网络凭借其「万能近似」的属性在函数近似方面无与伦比。在高级层面，神经网络可以构成黑箱函数近似器，它会学习如何根据大量训练数据点来参数化单个函数。

除了使用神经网络这种参数化的方法逼近一个函数，我们还可以根据随机过程执行推断以进行函数回归。随机过程会从概率的角度选择目标函数的可能分布，因而也能通过样本采样逼近真实的目标函数，随机过程在强化学习与超参数搜索方面比较常用。随机过程中最常见的实例就是高斯过程（GP），这种模型与神经网络有着互补的属性：高斯过程不需要昂贵的训练阶段，并且可以直接根据一些观察值对潜在的真实函数进行推断，这使得这种方法在测试阶段有非常灵活的属性。

但是高斯过程也有着很多局限性，首先 GP 在计算上是非常昂贵的。在原始方程中，计算复杂度随数据点的数量增加成立方地增加，即使在当前最优的近似方法中，那也是成平方地增加。此外，可用的核函数通常在函数形式上受到很大的限制，并且需要额外的优化过程来确定最合适的核函数，其可以看作高斯过程的超参数。

而最近 DeepMind 连发两篇论文探讨结合神经网络与高斯过程的方法，他们首先在论文《Neural Processes》中探讨了使用神经网络学习逼近随机过程的方法，随后又在论文《Conditional Neural Processes》讨论了结合神经网络与高斯过程解决监督学习问题的端到端的方法。

在论文《Neural Processes》中，DeepMind 介绍了基于神经网络的形式化方法，以学习随机过程的近似，他们将这种方法称之为神经过程（NP）。NP 能展示 GP 的一些基本属性，即学习目标函数的一个分布以逼近真实函数，NP 能根据上下文观察值估计其预测的不确定性，并将一些工作负载从训练转移到测试的过程中，这使得模型拥有更高的灵活性。更重要的是，NP 以高效计算的方式生成预测。给定 n 个上下文点和 m 个目标点，使用已训练 NP 进行推断对应着深度网络中的前向传播过程，它的时间复杂度为 O(n+m) 而不是经典高斯过程所需要的 O((n+m)^3)。此外，模型可以直接通过数据学习隐式的核函数，从而克服很多函数设计上的限制。

在论文《Conditional Neural Processes》中，DeepMind 提出了一族模型，可用于解决监督学习问题，并提供了端到端的训练方法，其结合了神经网络和类似高斯过程的特征。DeepMind 称这族神经网络为条件神经过程（CNP），以表明它们在给定一系列观察数据时定义函数的条件分布。CNP 对观察数据的依赖由一个神经网络参数化，其在输入的置换排列下保持不变。该架构的测试时间复杂度为 O(n+m)，其中 n、m 分别是观察样本数和目标数。

论文：Neural Processes

论文地址：https://arxiv.org/abs/1807.01622

摘要：神经网络是一类参数化函数，可以通过梯度下降来高精度地逼近标记数据集。另一方面，高斯过程（GP）是一种概率模型，其定义了可能函数的分布，并通过概率推理规则和数据来更新。GP 是概率性、数据高效和灵活的，然而它们的计算很昂贵，因而应用受限。我们引入了一类神经隐变量模型，称为神经过程（NP），其结合了两者的优点。和 GP 类似，NP 定义了函数的分布，可以快速适应新的观察数据，并可以评估预测的不确定性。类似神经网络，NP 在训练和评估过程中的计算是高效的，并且能学习将先验概率引入到数据中。我们在一系列学习任务上展示了 NP 的性能，包括回归和优化，并和相关文献的模型进行对比。

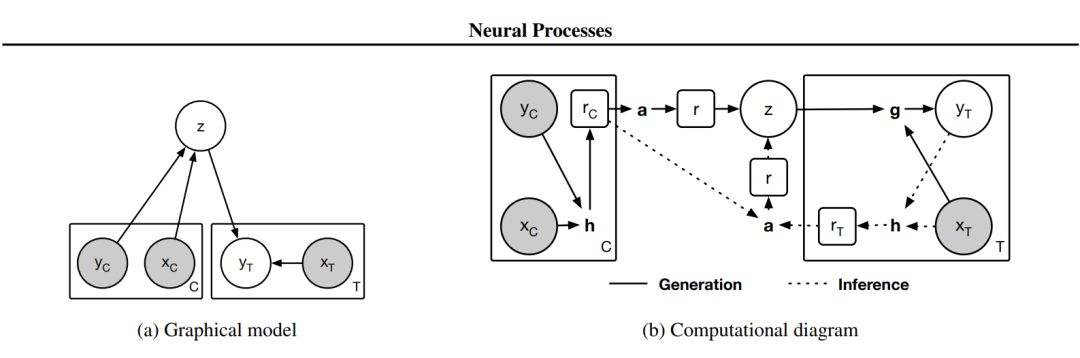
图 1：神经过程模型。（a）神经过程的图模型。x 和 y 对应着 y = f(x) 的数据，C 和 T 分别是上下文点和目标点的数量，而 z 表示全局隐变量。此外，灰色背景表示变量是已经观察到的。（b）为实现神经过程的计算图。圆圈里面的变量对应着这（a）中图模型的变量，方框里面的变量为 NP 的中间表征。而没有框的加粗字母分别表示以下计算模块：h 为编码器、a 为汇集器（aggregator）、g 为解码器。在该实现中，h 和 g 分别对应神经网络，而 a 对应均值函数。最后，实线描述了生成过程，而虚线描述了推断过程。

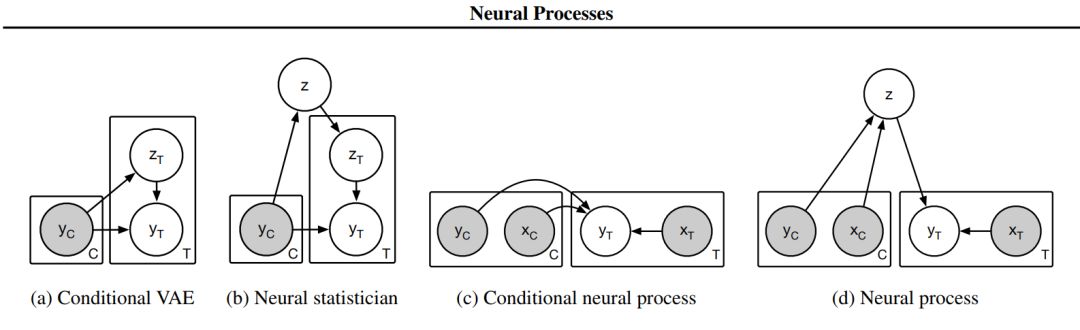
图 2：相关模型（a-c）和神经过程（d）的图模型。灰色阴影表示变量已被观察。C 代表上下文变量，T 代表目标变量（即给定 C 的预测变量）。

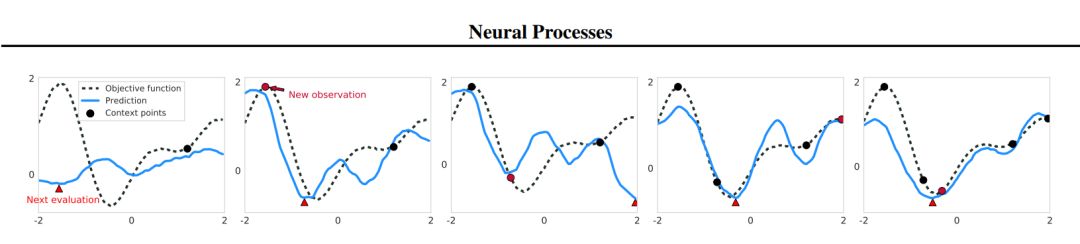
图 5：在 1-D 目标函数利用神经过程的 Thompson sampling。图中展示了五次迭代的优化过程。每个预测函数（蓝色）通过采样一个隐变量进行绘制，以上下文点数的增加为条件（黑色圆）。真实函数由一个黑色点线表示。红色三角形对应采样 NP 曲线的最小值的下一个评估点。下一次迭代中的红色圆对应该评估点及其真值，作为 NP 的下一个上下文点。

论文：Conditional Neural Processes

论文地址：https://arxiv.org/abs/1807.01613

摘要：深度神经网络在函数近似中表现优越，然而通常对每个新函数它们都需要从零开始学习。另一方面，贝叶斯方法，例如高斯过程（GP）利用了先验知识在测试时快速推理新函数的形状。不过 GP 的计算很昂贵，并且设计合适的先验可能很困难。在本文中我们提出了一族神经模型：条件神经过程（CNP），其结合了前述两者的优点。CNP 由随机过程例如高斯过程的灵活性所启发，但其结构是神经网络式的，并通过梯度下降来训练。CNP 仅观察了少量训练数据点之后就可以执行准确的预测，并能扩展到复杂函数和大规模数据集上。我们在一系列标准的机器学习任务（包括回归、分类和图像补全）上展示了该方法的性能和通用性。

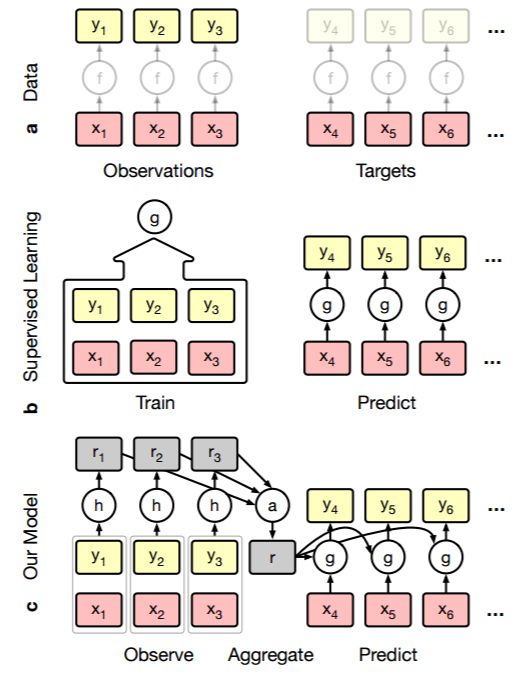
图 1：条件神经过程。a）数据描述；b）传统监督深度学习模型的训练方式；c）本文提出的模型。

4. 实验结果

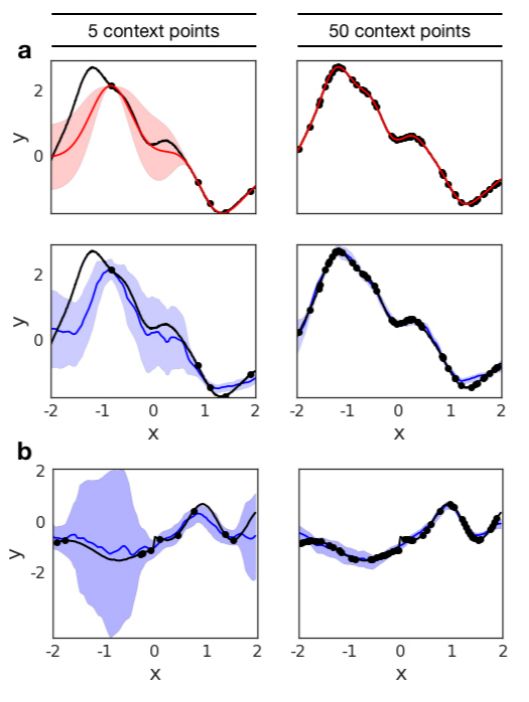
图 2：1-D 回归。用 5 个（左列）和 50 个（右列）上下文点（黑点）得到的 1-D 曲线（黑线）回归结果。前两行展示了 GP（红色）和 CNP（蓝色）进行回归的预测平均值和方差，它们只使用单个潜在核函数。最后一行展示了用交换核参数得到的 CNP 预测曲线。

图 3：在 MNIST 上的像素级图像回归。左：不同观察样本数下的图像回归的两个示例。研究者向模型提供了 1、40、200 和 728 个上下文点（顶行），并查询完整的图像。图中展示了每张图像在每个像素位置得到的平均值（中行）和方差（底行）。右：随着观察样本数的增加的模型准确率变化，其中两条曲线分别是随机（蓝色）或按最高方差（红色）选择像素。

图 4：在 CelebA 上的像素级图像补全。不同观察样本数下的 CelebA 图像回归的两个示例。研究者向模型提供 1、10、100 和 1000 个上下文点（顶行）并查询完整的图像。图中展示了每张图像在每个像素位置得到的平均值（中行）和方差（底行）。

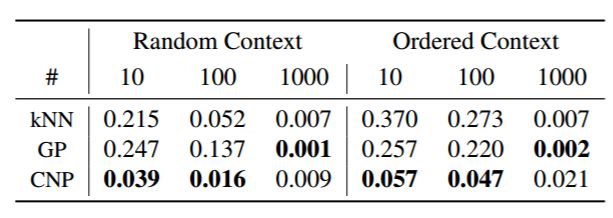
表 1：在 Celeb A 数据集上随着上下文点的增加（10、100、1000）在图像补全任务上的所有图像像素的像素级均方误差。这些点或者是随机选择的，或者是按左下到右上的顺序选择的。在提供更少的上下文点的情况下，CNP 超越了 kNN 和 GP。此外，CNP 在点选择顺序排列的情况下也能表现良好，而 GP 和 kNN 在点顺序排列的时候表现变差很多。

本文为机器之心编译，转载请联系本公众号获得授权。

✄------------------------------------------------

加入机器之心（全职记者 / 实习生）：hr@jiqizhixin.com

投稿或寻求报道：content@jiqizhixin.com

广告 & 商务合作：bd@jiqizhixin.com