会员服务 ·

【自动化】详解PID调节的基本概念、参数与调试方法，清晰易懂！

2018 年 12 月 20 日 产业智能官

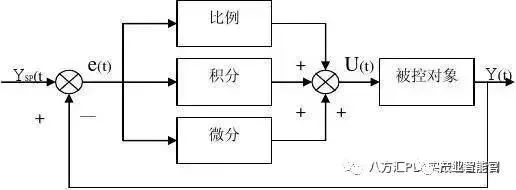
PID控制，实际中也有PI和PD控制。PID控制器就是根据系统的误差，利用比例、积分、微分计算出控制量进行控制的。PID控制器的参数整定是控制系统设计的核心内容！

如果你从来没有接触过PID，看完这篇文章你就会明白PID控制到底是怎么回事了！

PID是比例、积分、微分的简称，PID控制的难点不是编程，而是控制器的参数整定。参数整定的关键是正确地理解各参数的物理意义。

1. 比例控制

比例控制是最常用的控制手段之一，比方说我们控制一个加热器的恒温100度，当开始加热时，离目标温度相差比较远，这时我们通常会加大加热，使温度快速上升，当温度超过100度时，我们则关闭输出，通常我们会使用这样一个函数

e(t) = SP – y(t)-

u(t) = e(t)*P

SP——设定值

e(t)——误差值

y(t)——反馈值

u(t)——输出值

P——比例系数

比例控制的比例系数如果太小，即调节后的电位器转角与位置L的差值太小，调节的力度不够，使系统输出量变化缓慢，调节所需的总时间过长。比例系数如果过大，即调节后电位器转角与位置L的差值过大，调节力度太强，将造成调节过头，甚至使温度忽高忽低，来回震荡。

增大比例系数使系统反应灵敏，调节速度加快，并且可以减小稳态误差。但是比例系数过大会使超调量增大，振荡次数增加，调节时间加长，动态性能变坏，比例系数太大甚至会使闭环系统不稳定。

单纯的比例控制很难保证调节得恰到好处，完全消除误差。

2.积分控制

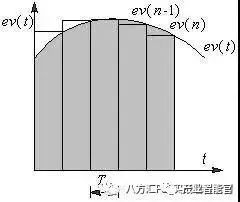
PID控制器中的积分对应于图1中误差曲线与坐标轴包围的面积(图中的灰色部分)。PID控制程序是周期性执行的，执行的周期称为采样周期。计算机的程序用图1中各矩形面积之和来近似精确的积分，图中的TS就是采样周期。

PID控制器输出中的积分部分与误差的积分成正比。因为积分时间TI在积分项的分母中，TI越小，积分项变化的速度越快，积分作用越强。

3.PI控制

如果控制器有积分作用(例如采用PI或PID控制)，积分能消除阶跃输入的稳态误差，这时可以将比例系数调得小一些。

如果积分作用太强(即积分时间太小)，相当于每次微调电位器的角度值过大，其累积的作用会使系统输出的动态性能变差，超调量增大，甚至使系统不稳定。积分作用太弱(即积分时间太大)，则消除稳态误差的速度太慢，积分时间的值应取得适中。

4.微分作用

误差的微分就是误差的变化速率，误差变化越快，其微分绝对值越大。误差增大时，其微分为正;误差减小时，其微分为负。控制器输出量的微分部分与误差的微分成正比，反映了被控量变化的趋势。

有经验的操作人员在温度上升过快，但是尚未达到设定值时，根据温度变化的趋势，预感到温度将会超过设定值，出现超调。于是调节电位器的转角，提前减小加热的电流。这相当于士兵射击远方的移动目标时，考虑到子弹运动的时间，需要一定的提前量一样。

5.采样周期

6.PID参数的调整方法

在整定PID控制器参数时，可以根据控制器的参数与系统动态性能和稳态性能之间的定性关系，用实验的方法来调节控制器的参数。有经验的调试人员一般可以较快地得到较为满意的调试结果。在调试中最重要的问题是在系统性能不能令人满意时，知道应该调节哪一个参数，该参数应该增大还是减小。

为了减少需要整定的参数，首先可以采用PI控制器。为了保证系统的安全，在调试开始时应设置比较保守的参数，例如比例系数不要太大，积分时间不要太小，以避免出现系统不稳定或超调量过大的异常情况。给出一个阶跃给定信号，根据被控量的输出波形可以获得系统性能的信息，例如超调量和调节时间。应根据PID参数与系统性能的关系，反复调节PID的参数。

7.PID校正网络分析

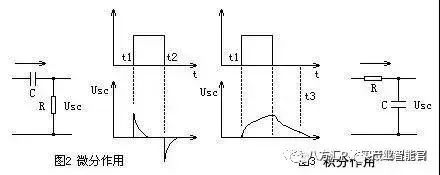
　微分：　

从电学原理我们知道，见图2，当脉冲信号通过RC电路时，电容两端电压不能突变，电流超前电压90°，输入电压通过电阻R向电容充电，电流在t1时刻瞬间达到最大值，电阻两端电压Usc此刻也达到最大值。随着电容两端电压不断升高，充电电流逐渐减小，电阻两端电压Usc也逐渐降低，最后为0，形成一个锯齿波电压。这种电路称为微分电路，由于它对阶跃输入信号前沿“反应”激烈，其性质有加速作用。

　积分：　

我们再来看图3，脉冲信号出现时，通过电阻R向电容充电，电容两端电压不能突变，电流在t1时刻瞬间达到最大值，电阻两端电压此刻也达到最大值。电容两端电压Usc随着时间t不断升高，充电电流逐渐减小，最后为0，电容两端电压Usc也达到最大值，形成一个对数曲线。这种电路称为积分电路，由于它对阶跃输入信号前沿“反应”迟缓，其性质是“阻尼”缓冲作用。

PID控制器参数整定的一般方法：

现在一般采用的是临界比例法。利用该方法进行 PID控制器参数的整定步骤如下：(1)首先预选择一个足够短的采样周期让系统工作；(2)仅加入比例控制环节，直到系统对输入的阶跃响应出现临界振荡，记下这时的比例放大系数和临界振荡周期；(3)在一定的控制度下通过公式计算得到PID控制器的参数。

在PID参数进行整定时如果能够有理论的方法确定PID参数当然是最理想的方法，但是在实际的应用中，更多的是通过凑试法来确定PID的参数。

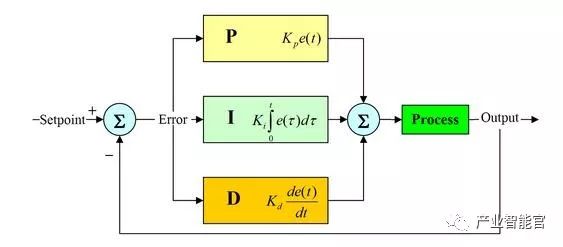
深度理解PID算法

PID控制器调节输出，保证偏差(e)为零，使系统达到稳定状态。偏差(e)是设定值(SP)和过程变量(PV)的差。PID控制的原理基于下面的算式；输出M(t)是比例项、积分项和微分项的函数。

其中：

M (t) 是作为时间函数的回路输出

K C 是回路增益

e 是回路误差(设定值和过程变量之间的差)

M initial 是回路输出的初始值

为了能让数字计算机处理这个控制算式，连续算式必须离散化为周期采样偏差算式，才能用来计算输出值。数字计算机处理的算式如下：

其中：

M n 是在采样时刻n，PID回路输出的计算值

K C 是回路增益

e n 是采样时刻n的回路误差值

e n -- 1 是回路误差的前一个数值(在采样时刻n--1)

e x 是采样时刻x的回路误差值

K I 是积分项的比例常数

M initial 是回路输出的初始值

K D 是微分项的比例常数

从这个公式可以看出，积分项是从第1个采样周期到当前采样周期所有误差项的函数。微分项是当前采样和前一次采样的函数，比例项仅是当前采样的函数。在数字计算机中，不保存所有的误差项，实际上也不必要。

由于计算机从第一次采样开始，每有一个偏差采样值必须计算一次输出值，只需要保存偏差前值和积分项前值。作为数字计算机解决的重复性的结果，可以得到在任何采样时刻必须计算的方程的一个简化算式。简化算式是：

其中：

M n 是在采样时间n时，回路输出的计算值

K C 是回路增益

e n 是采样时刻n的回路误差值

e n -- 1 是回路误差的前一个数值(在采样时刻n--1)

K I 是积分项的比例常数

MX 是积分项的前一个数值(在采样时刻n -- 1)

K D 是微分项的比例常数

CPU实际使用以上简化算式的改进形式计算PID输出。这个改进型算式是：

其中：

Mn 是在采样时间n时的回路输出的计算值

MP n 是在采样时间n时回路输出比例项的数值

MI n 是在采样时间n时回路输出积分项的数值

MDn 是在采样时间n时回路输出微分项的数值

工业互联网

产业智能官 AI-CPS

加入知识星球“产业智能研究院”：先进产业OT（工艺+自动化+机器人+新能源+精益）技术和新一代信息IT技术（云计算+大数据+物联网+区块链+人工智能）深度融合，在场景中构建状态感知-实时分析-自主决策-精准执行-学习提升的机器智能认知计算系统；实现产业转型升级、DT驱动业务、价值创新创造的产业互联生态链。