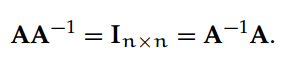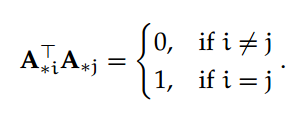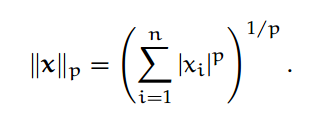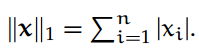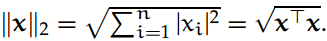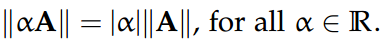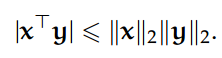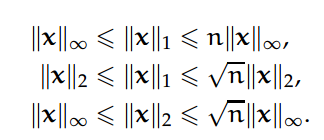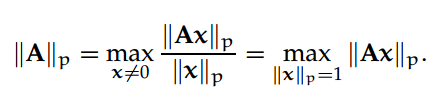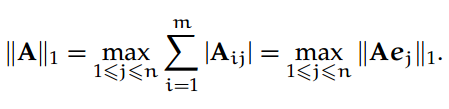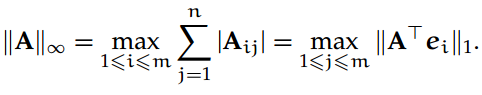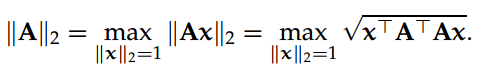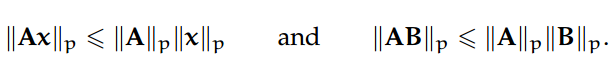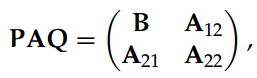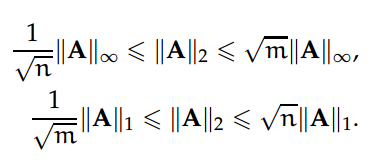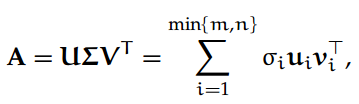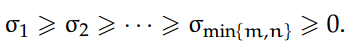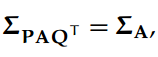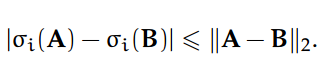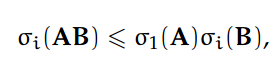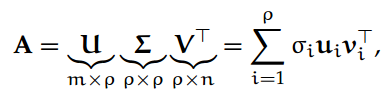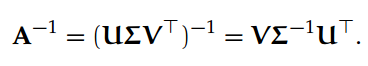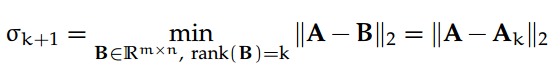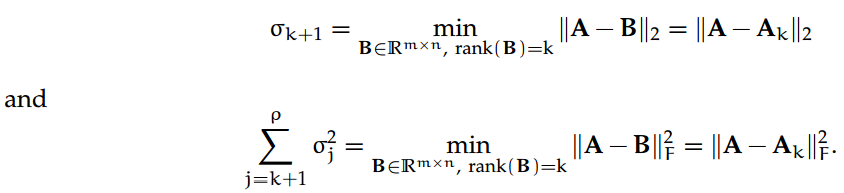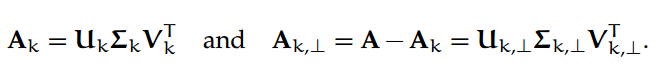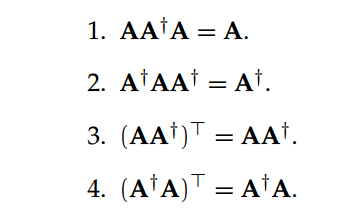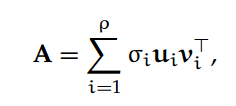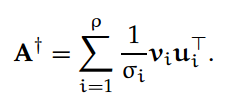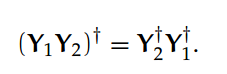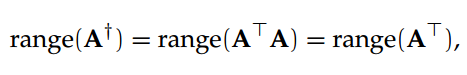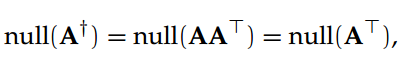开发者必读：计算机科学中的线性代数

选自arXiv

作者：Petros Drineas、Michael W. Mahoney

机器之心编译

参与：李泽南、刘晓坤、蒋思源

矩阵计算在计算机科学中占有举足轻重的地位，是每个开发者都需要掌握的数学知识。近日，来自普渡大学的 Petros Drineas 与 UC Berkeley 的 Michael Mahoney 提交了一篇概述论文《Lectures on Randomized Numerical Linear Algebra》可以作为线性代数知识的参考资料，本文将对其中的部分内容（主要为第二章：线性代数）进行简单介绍。

论文链接：https://arxiv.org/pdf/1712.08880.pdf

简介

矩阵在计算机科学、统计学和应用数学中占有独一无二的地位。一个 m×n 矩阵可以对 m 个对象（每个对象由 n 个特征描述）在有限单元网格中的离散微分算子信息进行描述；一个 n×n 正定矩阵可以编码所有 n 对象配对之间的相关性，或者网络中所有 n 节点对之间的边连通性等等。受科学和计算机技术发展的影响，近年来我们见证了矩阵算法理论和实践上令人兴奋的发展。其中最值得注意的是随机化的使用——通常假设由于生成机制的原因，输入数据存在噪声——它可以作为算法或计算资源用于开发和提升基础矩阵问题如矩阵乘法、最小二乘（LS）近似、低阶矩阵近似等算法。

随机数值线性代数（RandNLA）是一个跨学科的研究领域，利用随机化作为计算资源来开发用于大规模线性代数问题的提升算法。从基础的角度来看，RandNLA 源自理论计算机科学（TCS），并与数学有着很深的联系（凸面分析、概率论、度量嵌入理论），也与应用数学相关（科学计算、信号处理、数值线性代数）。从应用层面来看，RandNLA 是机器学习、统计和数据分析的重要新工具。很多精心设计的实现已经在大量问题上超越了高度优化的软件库，如最小二乘回归，同时也具有相当的扩展性、平行计算和分布能力。此外，RandNLA 为现代大规模数据分析提供了良好的算法和统计基础。

这一章将作为对三种基本 RandNLA 算法的独立的入门介绍，分别是随机矩阵乘法（randomized matrix multiplication）、随机最小二乘解算器（randomized least-squares solvers），以及用一个随机算法计算矩阵的低秩近似。因此，这一章和很多应用数学的领域有非常强的联系，特别是它和这一卷的其它许多章节都有很强的联系。最重要的是，其中分别包含了 G. Martinsson 的工作，他利用这些方法开发了改进的低秩矩阵近似解算器 [2]；R. Vershynin 的工作，他开发了概率论工具用于分析 RandNLA 算法 [3]； J. Duchi 的工作，他以互补的方式利用随机方法求解更通用的优化问题 [4]；以及 M. Maggioni 的工作，他以这些方法作为更复杂的多尺度方法的基础模块 [5]。

本论文将在第二节中概述基本的线性代数知识；在第三节概述离散概率的基本知识；在第四节介绍矩阵乘法的随机算法；在第五节介绍最小二乘回归问题的随机算法；在第六节介绍低秩近似的随机算法。最后我们还介绍了两个其它关于 RandNLA 的导论资源 [6,7]，供感兴趣的读者参考。

2 线性代数

在这一节，我们将简要概述基本的线性代数属性和在这一章中将用到的数学符号。我们假定读者具备线性代数的基础（例如，向量的内积和叉积，基本矩阵运算如加法、标量乘法、转置、上/下三角矩阵，矩阵-向量乘法，矩阵乘法，矩阵的迹等）。

2.1 基础

我们将完全聚焦于线性空间中的矩阵和向量。我们使用符号 x ∈ R^n 表示 n 维向量，注意向量都是以粗体小写字母书写。这里假定所有的向量都是列向量，除非特别说明。所有元素为零的向量用 0 表示，所有元素为 1 的向量用 1 表示（类似 Broadcasting）；维度会隐含在上下文中或显式地用下标表示。

我们将使用粗体大写字母表示矩阵，例如 A ∈ R^mxn 表示一个 mxn 阶的矩阵；用 A_i* 表示 A 的第 i 行的行向量，用 A_*i 表示 A 的第 i 列的列向量。单位矩阵表示为 I_n，其中 n 是矩阵的行数和列数。最后，我们用 e_i 表示 I_n 的第 i 列，即第 i 个规范基。

逆矩阵：如果存在一个逆矩阵 A^-1 ∈ R^mxn 满足以下条件，那么矩阵 A ∈ R^mxn 被称为非奇异的或可逆的：

如果 A 的所有列向量（或行向量）线性无关，那么 A 是可逆的。换句话说，不存在一个非零向量 x ∈ R^n 使得 Ax=0。可逆矩阵的标准性质有： (A^−1 )^⊤ = (A^⊤)^−1 = A^−⊤（A 逆的转置等于 A 转置的逆）和 (AB)^−1 = B^−1* A^−1（A 左乘 B 的逆等于 B 逆左乘 A 逆。注：微信表达式展示不便，准确表达式请查看原材料）。

正交矩阵：如果矩阵 A ∈ R^n×n 满足 A^⊤=A^−1，则称 A 为正交矩阵。等价地说，对所有 i , j 属于 [1,n]，正交矩阵满足：

对于 A 的行向量，上述性质同样满足。即 A 的所有列（或行）向量都是两两正交或互成法向量。

QR 分解：任意的矩阵 A ∈ R^n×n 都可以分解成一个正交矩阵和一个上三角矩阵的乘积：A=QR

其中 Q ∈ R^n×n 是正交矩阵，R ∈ R^n×n 是上三角矩阵。QR 分解在求解线性方程组的时候很有用，它的计算复杂度为 O(n^3)，并且是数值稳定的。为了用 QR 分解求解线性方程组 Ax=b，我们首先对等式两边同时左乘一个 Q^⊤，即 Q^⊤QRx = Rx = Q^⊤b。然后，我们用反向代入求解 Rx = Q^⊤b。

2.2 范数

范数（Norms）被用于度量矩阵的大小，或者相应地，度量向量的长度。范数是一个函数，它将 R^mxn（或 R^n）映射到 R。形式地说：

定义 1：任何函数满足 || · ||: R^m×n → R 和下列性质，则称为一个范数：

• 非负性：|| A ||≥0；|| A ||=0 当且仅当 A=0；

• 三角不等律：|| A+B ||≤|| A ||+|| B ||；

• 标量乘法律：|| αA ||=|α| || A ||，α∈R。

可以很容易地证明以下两个性质：

• || A ||=|| -A ||

• | || A ||-|| B || | ≤ || A-B ||

第二个性质被称为倒三角型不等式。

2.3 向量范数

若给定 n 维向量 x 和一个整数 p > 1，我们可以定义向量 p-范数为：

最常见的向量 p-范数为：

• 1-范数：

• 欧几里德（2）范数：

• 无穷（最大）范数：

若给定 n 维向量 x、y，我们可以使用 p-范数作为内积的上确界，即 Cauchy-Schwartz 不等式可以写为：

一般来说，该不等式给定了两个向量的欧几里德范数可以作为它们内积的上确界，Holder 不等式表明：

以下向量 p-范数的不等式性质可以轻易的证明：

2.4 归纳矩阵范数

给定一个 m×n 阶矩阵 A，和一个 p > 1 整数，我们定义矩阵的 p-范数为：

一般我们最常用的矩阵 p-范数为：

• 1-范数，取矩阵列加和绝对值的最大值：

• 无穷范数，取矩阵行加和绝对值的最大值：

• 2-范数，

这一系列的范数被称为「归纳（induced）」，因为它们是通过不取决于 A 和 p 的非零向量 x 而实现的。因此，一般存在一个单位范数向量（p-范数中的单位范数）x 令||A||p = ||Ax||p。归纳矩阵 p-范数遵循以下 submultiplicativity 法则：

此外，矩阵 p-范数对于矩阵的初等变换是不变的，即||PAQ||p = ||A||p，其中 P 和 Q 为对应维度的初等变换矩阵。同样，如果我们考虑矩阵分割：

那么子矩阵的范数就和全部矩阵的范数相关：即||B||p <= ||A||p。矩阵 p-范数间的以下关系可以相对简单地证明。若给定一个 m×n 阶矩阵，

此外，||A^T||1 = ||A||∞，||A^T||∞ = ||A||1。其中转置影响了矩阵的无穷范数和 1-范数，而不影响 2-范数，即||A^T||2 = ||A||2。同样，矩阵 2-范数并不会受到矩阵 pre(post)- multiplication 操作的影响，其中它的列（或行）为正交向量：||UAV^T||2 = ||A||2，其中 U 和 V 为对应维度的正交矩阵（U^T*U = I and V^T*V = I）。

2.6 奇异值分解

我们知道方阵可以分解为特征值与特征向量，但非方阵的矩阵并没不能实现特征值分解。因此奇异值分解（SVD）是每个矩阵中最重要的矩阵分解方式，因为不是所有的矩阵都能进行特征分解，但是所有的矩阵都能进行奇异值分解。

定义 6. 给定一个矩阵 A ∈ R^m×n，我们定义全 SVD 为：

其中 U ∈ R^m×m 和 V ∈ R^n×n 分别是包含 A 的左、右奇异向量的正交矩阵，Σ ∈ R^m×n 是对角矩阵，其中 A 的奇异值在主对角线上递减。

我们经常使用 u_i（或 v_j），i=1,..., m（或 j=1,..., n）来表示矩阵 U（或 V）的列。同样，我们将使用σ_i，i = 1,..., min{m, n} 来表示奇异值：

A 的奇异值是非负的，其数目等于 min{m, n}。A 的非零奇异值个数等于 A 的秩。由于正交不变性，我们得到：

其中 P 和 Q 是对应维度上的正交矩阵（P^TP = I 且 Q^TQ = I）。或者说，PAQ 的奇异值与 A 的奇异值相同。

涉及矩阵 A 和 B 的奇异值的以下不等式是非常重要的。首先，如果 A 和 B 都在 R^m×n 上，对于所有 i = 1, ... , min{m, n}，

第二，如果 A ∈ R^p×m 和 B ∈ R^m×n，对于所有 i = 1, ... , min{m, n}，

其中σ_1(A) = ||A||_2。我们经常对于仅保持非零奇异值和相应的（矩阵 A 的）左、右奇异向量感兴趣。给定矩阵 A ∈ R^m×n 和 rank(A)=ρ，我们可以定义它的稀疏 SVD。

定义 9. 给定矩阵 A ∈ R^m×n，秩为ρ ≤ min{m, n}，我们定义稀疏 SVD 为：

其中 U ∈ R^m×ρ和 V ∈ R^n×ρ是包含对应于非零奇异值的左、右奇异向量的两两正交列（即 U^TU = I 且 V^TV = I）的矩阵；Σ ∈ R^ρ×ρ是 A 的非零奇异值在对角线上递减的对角矩阵。

如果 A 是非奇异矩阵，我们可以使用 SVD 计算它的逆：

（如果 A 是非奇异的，那么它是方形和满秩的，在这种情况下，稀疏 SVD 和全 SVD 是一样的）众所周知，SVD 非常重要，任何矩阵的最佳 k 秩近似都可以通过 SVD 来计算。

定理 10. 让 A = UΣV^⊤ ∈ R^m×n 作为 A 的稀疏 SVD；设 k < rank(A) = ρ为整数，让

随后，

换句话说，上述定理指出，如果我们寻找一个矩阵 A 的 k 秩近似，使得「误差」矩阵的 2-范数或 Frobenius 范数最小化（即 A 和它的近似之间的差异最小化），随后我们需要保留 A 的最前 k 个奇异值和相应的左、右奇异向量。

我们会经常使用这些符号：让 U_k ∈ R^m×k（或 V_k ∈ R^n×k）表示矩阵 A 的最前 k 个左（或右）奇异向量的矩阵；让 Σ_k ∈ R^k×k 表示包含 A 的最前 k 个奇异值的对角矩阵。同样的，让 U_k,⊥ ∈ R^m×(ρ−k)（或 V_k,⊥ ∈ R^n×(ρ−k)）表示 A 的底部ρ-k 个非零左（或右）奇异向量的矩阵；然后令Σ_k,⊥ ∈ R^(ρ−k)×(ρ−k) 表示包含 A 的底部ρ-k 个奇异值的对角矩阵。然后，

2.9 Moore-Penrose 伪逆

对于非方矩阵而言，其逆矩阵是没有定义的。而一种非常出名的推广型矩阵求逆方法 Moore-Penrose 伪逆在这类问题上取得了一定的进展。形式上来说，若给定 m×n 阶矩阵 A，那么如果矩阵 A† 满足以下属性，它就是矩阵 A 的 Moore-Penrose 伪逆：

给定一个秩为ρ的 m×n 阶矩阵 A，它的稀疏奇异值分解可以表示为：

它的 Moore-Penrose 伪逆 A† 的稀疏奇异值分解可以表示为：

如果 A 为 n×n 阶满秩矩阵，那么 A† 就等于矩阵 A 的逆。如果 A 为 m×n 阶列满秩矩阵，那么 A†A 就等于 n 阶单位矩阵，AA†为矩阵 A 列上的投影矩阵。如果 A 为满行秩矩阵，那么 AA†就为 m 阶单位矩阵，A†A 为矩阵 A 行上的投影矩阵。

关于两个矩阵乘积的伪逆，有如下特别重要的属性：对于 m×p 阶矩阵 Y1 和 p×n 阶矩阵 Y2，且满足 Rank(Y1)=Rank(Y2)，即秩相等，[9, Theorem 2.2.3] 表明：

（我们强调秩相等的条件是非常重要的：因为两个矩阵相乘的逆总是等价于矩阵逆的相乘，但这个推断对于一般的 Moore-Penrose 伪逆 [9] 是不满足的）此外，Moore-Penrose 伪逆的基空间和所有实际的矩阵都有联系。给定一个矩阵 A 和 A 的 Moore-Penrose 伪逆 A†，A†的列空间可以定义为：

A†的列空间和零空间（null space）正交，A†的零空间可以定义为：

本文为机器之心编译，转载请联系本公众号获得授权。

✄------------------------------------------------

加入机器之心（全职记者/实习生）：hr@jiqizhixin.com

投稿或寻求报道：content@jiqizhixin.com

广告&商务合作：bd@jiqizhixin.com