天行见物理之三:浑行无穷
|作者:李轻舟 (《大学科普》编辑部)
驯乎玄,浑行无穷正象天。
—— 《太玄·玄首序》
济济京城内,赫赫王侯居。
冠盖荫四术,朱轮竟长衢。
朝集金张馆,暮宿许史庐。
南邻击钟磬,北里吹笙竽。
寂寂扬子宅,门无卿相舆。
寥寥空宇中,所讲在玄虚。
言论准宣尼,辞赋拟相如。
悠悠百世后,英名擅八区。
——左思《咏史·其四》
汉成帝永始二年( 公元前15年), 年近不惑的蜀郡扬雄( 字子云),北上长安,游于京师,经当国辅政的大司马车骑将军王音(出身魏郡元城王氏,王政君的堂兄弟)推荐,待诏承明殿。此后一年多的时间内,扬雄效仿蜀中前贤司马相如(南朝刘勰在《文心雕龙》中将二人并称“马扬”),连上《甘泉》《河东》《羽猎》三赋,讽劝成帝,遂“除为郎,给事黄门”(《汉书·扬雄传》),“得观书于石室”(扬雄《答刘歆书》),又结识了彼时尚在禁中校书的刘歆以及宿卫皇宫的新都侯王莽。
茂陵他日求遗稿,犹喜曾无封禅书。
——林逋《自作寿堂因书一绝以志之》
与贵为宗室的好友刘歆不同,扬雄并没有搭上外戚王莽崛起的顺风车,虽历经成、哀、平诸朝,“三世不徙官”(《汉书·扬雄传》)。直到王莽称帝的始建国元年(公元9年),年逾六旬的扬雄才凭“耆老久次”(年高德劭却久居下位)这等尴尬至极的理由升任中散大夫,还得依司马相如故事(遗稿《封禅》),上《剧秦美新》一篇叩谢天恩,极尽歌功颂德之能事——历仕四朝(南梁、北齐、北周、隋)的颜之推斥之为“ 德败《美新》”(《颜氏家训·文章》,刘歆则被颜氏抨击为“反覆莽世”),南宋朱熹更是在《通鉴纲目·汉纪》中以春秋笔法直书“莽大夫扬雄死”对其大加讥讽[1]。
图1 成都郫都区农科村的扬雄塑像
纵是难免卑躬屈节之嫌,暮年的扬雄仍旧仕宦不显,其身贫居陋室,其志恬淡自守,寂寂孤立于汉新禅代之际群小竞进的风潮之中——“冠盖满京华,斯人独憔悴”(《梦李白·其二》),数百年后杜甫感怀李白的名句,竟也是扬雄寄寓长安三十余年的生动写照。
阖天谓之宇,辟宇谓之宙。
—— 《太玄·玄摛》
扬雄少时在蜀中从游于道家高士严遵(字君平,本姓庄,《汉书》避明帝刘庄讳,改为严),继承了老庄学派世代传续的立身风范与形上追求,“为人简易佚荡,口吃不能剧谈,默而好深湛之思,清静亡为”(《汉书·扬雄传》)。在大汉帝国行将倾颓之际,本该悠游林泉的扬雄,舍弃巴山蜀水间的逍遥自在,投身魏阙丹陛下的波诡云谲——若非心有所系,何苦来哉?
图2 成都君平街今貌(周虹拍摄)
相较于朝堂之上的衮衮诸公,扬雄对权势总是若即若离。帝都的重重宫阙之内,扬雄念兹在兹,唯有兰台万卷——深藏禁中秘府的秦火孑遗。三十余年的宦海沉浮,扬雄之职守,一言以蔽之,“校书天禄阁上”(《汉书·扬雄传》)。
或问:“吾子少而好赋。”曰:“然。童子雕虫篆刻。”俄而曰:“壮夫不为也。”
——扬雄《法言·吾子》
这位未来将跻身汉赋四家的文豪,甚至不屑作以文辞见幸的司马相如第二。他有更大的“ 野心”——“张子侯曰:‘扬子云西道孔子也,乃貧如此。’吾应曰:‘子云亦东道孔子也。昔仲尼岂独是鲁孔子?亦齐楚圣人也。’”(桓谭《新论·启寤》)——其心之所系,乃是一个比同道刘歆的《三统历》体系更恢宏的“宇宙”。
古言天者有三家,一曰盖天,二曰宣夜,三曰浑天。
—— 《晋书·天文志》
在中国古人观念中,“天”兼具了灵性( 或者说神性) 和物性, 而“宇宙”(偏重于“宇”)往往可作“物性之天”的同义词。古来论天的诸派学说,其实就是宇宙学说。归结起来,不过宣夜、盖天和浑天三家。这三家学说,虽然常在典籍中并立,却不可等量齐观。
三家之一的宣夜说,到南朝祖暅(祖冲之之子)的时代,已沦落到“未尝闻也”(祖暅《天文录》,残篇见《太平御览》)的地步。据《晋书·天文志》记载,“宣夜之书亡,惟汉秘书郎郗萌记先师相传云:天了无质,仰而瞻之,高远无极,眼瞀精绝,故苍苍然也。譬之旁望远道之黄山而皆青,俯察千仞之深谷而窈黑,夫青非真色,而黑非有体也。日月众星,自然浮生虚空之中,其行其止皆须气焉。是以七曜或逝或住,或顺或逆,伏见无常,进退不同,由乎无所根系,故各异也。故辰极常居其所,而北斗不与众星西没也。摄提、填星皆东行,日行一度,月行十三度,迟疾任情,其无所系著可知矣。若缀附天体,不得尔也。”可知,“天”是由茫茫无形的“气”构成的,日月星辰浮于其中。这种观念可以归为朴素的自然哲学(也就是没有Principia Mathematica 的Philosophiæ Naturalis), 虽上承先秦道家(《庄子》《列子》等),下启宋明气学(张载、王夫之等),始终没有发展出可推演的数理结构以及可操作的观测模式,实难与盖天说和浑天说并称为系统的宇宙模型——最贴切的评价, 或许是泡利(W. Pauli) 的那句“Not even wrong”。相较而言,盖天与浑天两家是当得起泡利的一个“wrong”的。
地势极而南溟深,天柱高而北辰远。
——王勃《滕王阁序》
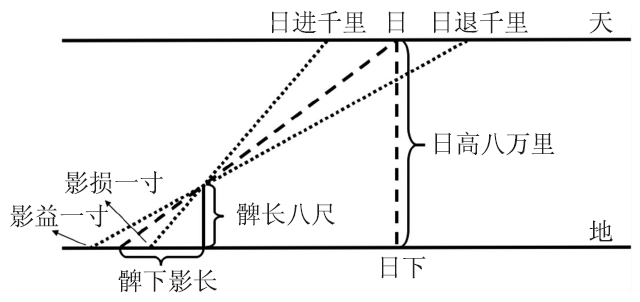
祖暅在《天文录》中将盖天说分成三派,“一云天如车盖,游乎八极之中;一云天形如笠,中央高而四边下;一云天如欹车盖,南高北下。”大致成书于两汉的《周髀算经》为盖天说建立了一个几何化的数理结构(故盖天说也可以称为周髀说),所谓“天象盖笠,地法覆盘。天离地八万里,冬至之日虽在外衡,常出极下地上二万里”(《周髀算经·卷下》)。在这样一个宇宙模型中,天(“盖笠”)与地(“覆盘”)是两个相互平行的平面,二者相距八万里。“八万里”这个数据当然不会来自实测,它是根据“周髀长八尺,勾之损益寸千里”(《周髀算经·卷上》)的假设(类似于欧氏几何的“公设”)推导而来的[2],其中蕴含的数理正是两个相似直角三角形的边长成比例——在地面立一个长为八尺的“髀”测日影(即立表测影之法),以髀下日影长为“勾”,髀长为“股”,构成一个小直角三角形。此时的“日高”即为天地距离,以“日下”(日在地面的投影点) 到髀下日影末端的距离为“勾”,以日高为股,又构成一个与前述小直角三角形相似的大直角三角形。“勾之损益寸千里”,即髀下日影损益一寸对应于日在天上进退一千里(即两个直角三角形的相似比为1 寸:1000 里),据此可得日高或天地相距八万里。又“勾股各自乘,并而开方除之”(《周髀算经·卷上》, 即运用“ 勾股定理”),还可求得髀下日影末端到日的距离。
图3 据“勾之损益寸千里”求日高的示意图(作者绘制)
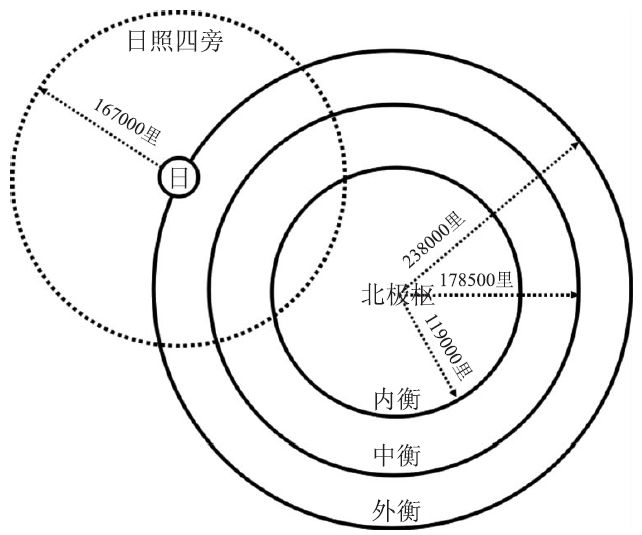
《周髀算经》为天上日行设置了“七衡六间”,即一组以“北极枢”(“天之中央”、北天极)为圆心的同心圆日道。夏至日道为“内衡”,冬至日道为“外衡”,春分和秋分的日道则在“中衡”,各依时节而定。按照这些设定,太阳永远在地平面上运动(日高恒为八万里)。为了解释昼夜交替,《周髀算经》不得不假设“日照四旁各十六万七千里”(《周髀算经·卷上》),在这个日照极限(也是人的目视极限,一个半径为167000 里的球)内为白昼,外为黑夜,其余天体的隐现亦同此理。对此,东汉王充给出了一个基于透视原理的解释,“日随天而转,非入地。夫人目所望,不过十里,天地合矣;实非合也,远使然耳。今视日入,非入也,亦远耳。”(《晋书·天文志》)
图4 日道与外衡日照极限的示意图(作者绘制)
北极枢之下(“极下”)有“璇玑”(或许是天旋之枢机),“其地高人所居六万里, 滂沱四颓而下”(《周髀算经·卷下》),即一个高出地面60000 里的锥状物,而天之中央的北极枢“ 亦高四旁六万里”(《周髀算经·卷下》)。在盖天模型中,北极枢和璇玑所在的中轴,是天上日月星辰轨道的圆心,也是天地或宇宙的中枢。这个大地中央的璇玑犹如天柱,好似上古传说中的“ 不周山” ——《淮南子·天文训》载“ 昔者共工与颛顼争为帝,怒而触不周之山, 天柱折,地维绝。天倾西北,故日月星辰移焉; 地不满东南,故水潦尘埃归焉。” 神话里, 共工怒触不周山,以致“ 天倾西北”,竟又与祖暅所谓“ 天如欹车盖, 南高北下”暗合了。
汉末,扬子云难盖天八事,以通浑天。
——《隋书·天文志》
《周髀算经》中的盖天宇宙模型出乎数理,却不合于天文(天象),甚至连日食和月食都解释不了。[3]扬雄本来信奉盖天说,“因众儒之说,以天为盖,常左旋,日月星辰随而东西。乃图画形体行度,参以四时历数,昏明昼夜,欲为世人立纪律, 以垂法后嗣” (《新论·离事》)。经过与桓谭的几番论辩(其中最有趣的一次是二人在宫内白虎殿廊庑下晒太阳,桓谭向扬雄生动地揭示了盖天说设定的太阳水平运动无法解释实际日影的明显变化),扬雄最终改旗易帜,作《难盖天八事》(见《隋书·天文志》),皈依浑天说……
谁能书阁下,白首《太玄经》。
——李白《侠客行》
扬雄后来在仿《论语》而作的《法言》中写道,“或问浑天,曰:落下闳营之,鲜于妄人度之,耿中丞象之,几乎!几乎!莫之能违也”(《法言·重黎》),指明了浑天说的渊源——《太初历》的制定与校验(落下闳和鲜于妄人各自在其中扮演了重要角色)。
历不能无差。今之学历者,但知历法,不知历理。能布算者,落下闳也;能推步者,甘石公也。落下闳但知历法,扬雄知历法又知历理。……扬雄作《玄》,可谓见天地之心者也。
——邵雍《皇极经世·观物外篇》
《周髀算经》中几何化的盖天模型,偏重空间(轨道)周期性,颇具古希腊风格。而《太初历》蕴含的宇宙体系,更偏重时间周期性,与之关系密切的浑天说,至少到扬雄的时代,其几何图像并不明显。浑天之“浑”,在扬雄等人的心目中,未必仅是可见的浑圆状貌,更可能是寓意抽象的周期轮回乃至宇宙的生生不息——“生生之谓易”(《易传·系辞》),为了阐发宇宙无穷(生化无穷而非时空无限), 刘歆援《易》而制《三统》,扬雄仿《易》而作《太玄》。
立志弃绝“丽靡之辞”后,扬雄转入了《太玄》(后亦称《太玄经》) 的创作。《玄首序》开宗明义,“驯乎玄,浑行无穷正象天。”扬雄以之为纲领,“大潭思浑天,参摹而四分之,极于八十一。旁则三摹九据,极之七百二十九赞,亦自然之道也”(《汉书·扬雄传》),推演出了八十一玄首的形式系统(比照《周易》的六十四卦):每首从上到下分方、州、部、家四重,每重有三种变化(即一、二和三,用短横的个数来表示),共有八十一(34=81)首;每首有九赞,共七百二十九赞。
八十一玄首自有一套生成模式,即“家,一置一,二置二,三置三;部,一勿增,二增三,三增六;州,一勿增,二增九,三增十八;方,一勿增,二增二十七,三增五十四”(《太玄·玄数》),用数学式可以表达为:
玄首之次序=家数×30+(部数-1)×31+(州数-1)×32+(方数-1)×33。
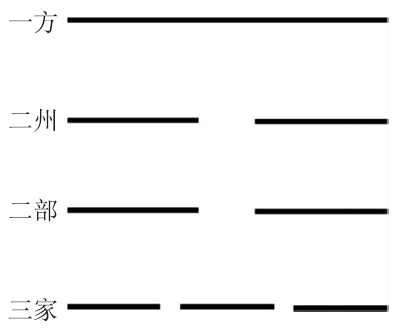
以图5 中的玄首“ 达” 为例, 将“一方二州二部三家”代入上式得15,即玄首达的次序。如果将一、二、三替换为0、1、2,上式可修正为:
玄首之次序=家数×30+部数×31+州数×32+方数×33。
据此,就可以将八十一玄首表示为一个简单的三进制序列,依次生成,连绵不断。这便是《太玄》体系内在的数理结构,也是扬雄版本的“万物皆数”——近代西方思想巨匠莱布尼兹(G. W. Leibniz)用二进制阐释的伏羲先天六十四卦亦有类似的生成模式。[4]
图5 玄首“达”的示意图
刘歆的《三统历》是对《太初历》的推广,扬雄的《太玄经》则是对《太初历》的抽象,“其用自天元推一昼一夜阴阳数度律历之纪, 九九大运, 与天终始。故《玄》三方、九州、二十七部、八十一家、二百四十三表、七百二十九赞,分为三卷,曰一二三,与《太初历》相庆, 亦有颛顼之历焉”(《汉书·扬雄传》)。玄首依次对应一岁时节,构成了一部抽象的历法[5],“八十一首岁事咸贞”(《太玄·玄首序》),周而复始,浑行无穷。扬雄将五德( 行)、五方、四季、干支、五音、五色、五味、五嗅、五形、五时、五脏、五侟、五性、五情、五事、五帝、五神等等悉数纳入“太玄”之中,先秦以降种种“天人图式”趋于综合,成就一个比《三统历》体系更恢宏的“宇宙”。
相如逸才亲涤器,子云识字终投阁。
——杜甫《醉时歌》
《太玄》在数理结构和表述形式上模仿《周易》,文辞艰深晦涩,内容庞杂纷繁,难为时人理解,招致不少讥嘲,扬雄专门为此写了《解嘲》和《解难》。甚至是同道刘歆也要来当面戏谑,“空自苦!今学者有禄利,然尚不能明《易》,又如《玄》何?吾恐后人用覆酱瓿也”(《汉书·扬雄传》),口吃的扬雄只好默而不语,一笑了之——“仆诚不能与此数公者并,故默然独守吾《太玄》。”(《解嘲》)
始建国三年(公元11 年),朝局的动荡终于波及天禄阁上,垂垂老矣的扬雄欲默守《太玄》而不得。国师刘歆的儿子刘棻因擅自造作符命触怒王莽,曾教授刘棻奇字(先秦古文的异体)的扬雄受到牵连。治狱使者前来捕拿之际,走投无路的扬雄,自天禄阁上纵身一跃……这一跃惊动了“故人”王莽,在他亲自过问下,不知情的扬雄得以免罪,逃过一劫。在这场有数百人死于非命的风波中,扬雄最终活了下来,“投阁几死”却传为笑柄……
惟寂寞,自投阁;爰清静,作符命。
—— 《汉书·扬雄传》所引京师流传的讥讽之语
一千三百多年后,罗贯中还要借舌战群儒的诸葛亮之口揶揄一番:“夫小人之儒,性务吟诗,空书翰墨;青春作赋,皓首穷经;笔下虽有千言,胸中实无一物。且如汉扬雄,以文章为状元,而屈身仕莽,不免投阁而死,此乃小人之儒也;虽日赋万言,何足道哉!”(嘉靖壬午本《三国演义》)——的确,对一个创造过“宇宙”的人,身后是非,何足道哉?
参考文献
[1]“莽大夫”后来成了对扬雄的特指,亦是屈膝变节者的代名词;又据《礼记·曲礼下》,“天子死曰崩,诸侯曰薨,大夫曰卒,士曰不禄,庶人曰死”,参见(东汉)郑玄注,(唐)陆德明释文. 宋本礼记(第一册). 北京:国家图书馆出版社,2017. 55
[2] 江晓原.《周髀算经》——中国古代唯一的公理化尝试. 自然辩证法通讯,1996,18(3):43
[3] 薄树人. 再谈《周髀算经》中的盖天说——纪念钱宝琮先生逝世十五周年. 自然科学史研究,1989,8(4):297
[4] Leibniz G,Explication de l'Arithmétique Binaire. Die Mathematische Schriften,ed. Gerhardt C. Berlin,1879. vol.7,p.223
[5] 黄开国.《太玄》与西汉天文历法.江淮论坛,1990,(2):61
本文选自《物理》2019年第3期