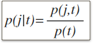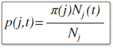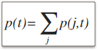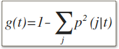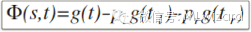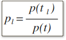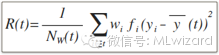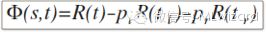决策树家族工具包代码实现（二）

2015 年 12 月 11 日 机器学习深度学习实战原创交流 塔拉夏的守护

距离上篇决策树的文章已经有段日子了,这次我们来聊聊CART和Random forest。之所以把CART和Random forest放在一起，完全是因为在rf的原文献中Leo breiman使用cart作为基树，其实我们完全可以使用任意一种决策树作为基树，例如，基于python的机器学习插件orange使用的就是c4.5。

既然原作者使用CART作为基树，那么我们在这里也把cart和rf的实现放在一起。首先来看看cart，cart的全称classification and regression tree分类回归树,是一个既能分类也能预测的强大工具。cart和id3、c4.5的最大区别是其本身是一个二叉树，每一个节点只分裂成左右两颗子树。同样，节点的分裂标准也不相同，id3、c4,5分别使用信息增益和信息增益比率来选择最佳特征值进行节点分裂而CART则使用impurity不纯度来进行节点分裂。对于目标变量分别为离散和连续时，不纯度的计算公式分别为：

Gini index:

节点t的Gini index g(t) 定义为：

其中i和j分别为待分裂离散特征的取值i和j(其他取值others),且：

其中：

: 为目标变量在取值j时的先验概率；

: 为节点t下目标变量取值j时的样本数量；

: 为根节点下目标变量取值j时的样本数量；

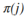
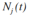
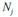
gini index也可以写成：

根据这个公式我们可以看出当目标变量的可能取值均匀分布时，gini index取得其在该节点上的最大值1-1/k, 其中k 为目标变量的可能取值个数。当所有样本的目标变量取值都相同时，则gini index取得最小值0。

据此，我们可以进一步定义离散目标变量的节点分裂指标：

公式一：

其中:

:节点t分裂后，分布到左子节点的样本比例；

:节点t分裂后，分布到右子节点的样本比例；

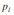
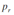
因此，分裂的标准是选取能使公式一的取值最大化，既最大化降低impurity统计量！

Least Squared Deviation:

对于连续类型的目标变量，使用least squared deviation(LSD) impurity统计量来进行节点分裂。

其中：

:节点t的加权样本数；

:样本i的权值；

:目标变量重复出现的频率；

:目标变量值；

:节点t下样本目标变量的加权平均；

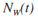
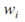
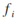
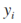
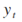
据此，我们可以进一步定义连续目标变量的节点分裂指标：

公式二：

怎么理解purity纯度和impurity不纯度这两个词呢？

我们可以把purity理解为样本间目标变量的相似程度，在一个完全纯的树节点上所有样本的目标变量具有相同的值。

CART的建树步骤如下：

1.对于每一个特征，寻找最佳分裂点：

连续特征：首先对该特征的所有取值进行从小到大排序，然后依次选取每一个值作为分裂点并根据公式二来计算分裂后的左右子节点的impurity统计量，最后选取使得节点分裂后impurity统计量下降最大的值作为该特征的最佳分裂点；
离散特征：首先对该离散特征的每一个取值进行去重并罗列，依次选取每一个取值作为分裂点，其余取值统统当作“others”来对待，换而言之原样本在该特征维度上被划分为两个子集subset。然后计算每一个取值作为分裂点后左右自节点的impurity统计量，最后选取使得节点分裂后impurity统计量下降最大的值作为该离散特征的最佳分裂点；

2.确定节点的最佳分裂点：

综合所有特征的最佳分裂点，选取使得impurity统计量下降最大的特征的最佳分裂点作为节点的最佳分裂点；

3.检查停止条件：

如果不触发停止条件，则节点被2中的方法分裂为两个子节点；

4.递归。

对每一个子节点，使用3进行节点分裂。

停止条件：

停止条件决定如何停止节点分裂，CART算法会持续进行树的生长直到所有的叶子节点都满足至少一种停止条件！

节点纯度100%，该节点下所有样本的目标变量值都相同；
节点下所有样本的待选特征都具有相同的值；
当前节点所处的深度达到树的指定最大深度；
节点下的样本数量少于指定的最小父节点/样本量；
节点分裂后产生的子节点下的样本数量少于指定的最小子节点/样本量；
节点分裂后产生的impurity统计量下降小于指定的最小impurity差；

代码实现(Python):

#首先引入相关模块，numpy是python 的一个第三方模块，提供多种高效的线性代数计算。注意到，引入了上一篇中的c45模块，主要是为了使用其中的训练集和测试集生成函数。

import bumpy as np

import operator

import C45

import copy

＃初始化必要参数，对于离散特征，存储其唯一取值对于后续计算会很方便

''will implement CART'''

class CART:

def __init__(self,target_type,features):

self.targetType=target_type

self.N=0

'''for classification only,unique values of all features, including the class'''

self.uniqueDiscValue={}

'''description of the features used for constructing tree'''

self.features=features

'''features used for constructing tree'''

self.featurUniqueDiscValue={}

＃从文本文件加载原始数据，对连续特征和离散特征分别进行相应处理

'''return dataSet, continues features are treated as floats'''

'''discrete features are encoded as ints, ex:1,2,3'''

def loadFromFile(self,filename):

dataSet=[]

'''store the discrete feature mapping,each unique discrete feature will have a unique key'''

'''{feature_n:[A,B,C]}, each discrete value in the data set will be replaced by the index of the unique set'''

dis_dic={}

f=open(filename,'r')

contiSet=[i for i in range(len(self.features)) if self.features[i][1]=="continuous"]

discSet=[i for i in range(len(self.features)) if self.features[i][1]=="discrete"]

for idx in range(len(self.features)):

dis_dic[idx]=[]

'''the class column's index is len(features)'''

dis_dic[len(self.features)]=[]

'''{feature_n:[A,B,C]}'''

for line in f:

t=line.strip('.\n').split(',')

for idx in range(len(t)):

'''generate unique value list of features'''

if (t[idx]!="?" and t[idx] not in dis_dic[idx]):

dis_dic[idx].append(t[idx])

self.uniqueDiscValue=copy.deepcopy(dis_dic)

f=open(filename,'r')

for line in f:

t=line.strip('.\n').split(',')

if "?" not in t:

d=[dis_dic[idx].index(t[idx]) for idx in range(len(t))]

if len(t)!=0:

dataSet.append(d)

return dataSet

＃根据特征取值当前节点下的样本数据集分裂，产生左右两个节点分别包含两组子数据集

'''this function assumes that the dataSet is formed using numpy array'''

def binSplitDataSet(self,dataSet,feature,value,feature_type):

mat0=None;mat1=None

if feature_type=="continuous":

mat0=dataSet[np.nonzero(dataSet[:,feature]>value)[0],:][0]

mat1=dataSet[np.nonzero(dataSet[:,feature]<=value)[0],:][0]

elif feature_type=="discrete":

mat0=dataSet[np.nonzero(dataSet[:,feature]==value)[0],:][0]

mat1=dataSet[np.nonzero(dataSet[:,feature]!=value)[0],:][0]

else:

print "illegal feature type!!"

return None,None

return mat0,mat1

＃对于离散类型的目标变量，每个节点都应该有一个决策分类，这样才符合mdl（minimum descriptive length）最小描述长度准则。因此，我们使用该节点下最常见的类标签作为输出

def majorityCnt(self,classList):

classCount={}

for vote in classList:

if vote not in classCount.keys():

classCount[vote]=0

classCount[vote]+=1 sortedClassCount=sorted(classCount.iteritems(),key=operator.itemgetter(1),reverse=True)

return sortedClassCount[0][0]

'''return the majority count of class labels'''

def claLeaf(self,dataSet):

return self.majorityCnt(dataSet[:,-1].T.tolist()[0])

＃对于连续类型的目标变量，使用该节点下样本目标变量取值的平均值作为输出

'''the mean of last column'''

def regLeaf(self,dataSet):

return np.mean(dataSet[:,-1])

＃当目标变量为离散类型时，使用gini index来计算impurity统计量

'''calculate gini index'''

def GiniIndex(self,dataSet):

m,n=np.shape(dataSet)

Gini=0

p_c_t_list=[]

if len(set(dataSet[:,-1].T.tolist()[0]))==1:

return 0

for c in set(dataSet[:,-1].T.tolist()[0]):

N_t=len(dataSet[np.nonzero(dataSet[:,-1]==c)[0],:][0])

p_c_t=float(N_t)/m

p_c_t_list.append(p_c_t)

sigma_p=0

for p in p_c_t_list:

sigma_p+=p*p

Gini=1-sigma_p

return Gini

＃当目标变量为连续类型时，使用总方差（为简单起见原公示二中权重和频率参数都用1来代替）来计算impurity统计量

'''最后一列的总方差'''

def regErr(self,dataSet):

return np.var(dataSet[:,-1])*np.shape(dataSet)[0]

＃计算最佳分裂点

def chooseBestSplit(self,dataSet, leafType, impurity, ops=(0.1,1)):

tolS=ops[0];tolN=ops[1]

if len(set(dataSet[:,-1].T.tolist()[0]))==1:

return None, leafType(dataSet)

m,n=np.shape(dataSet)

if n==1:

print "no more feature to split!"

return None, leafType(dataSet)

g=impurity(dataSet)

bestS=np.NINF;bestIndex=0;bestValue=0

for featIndex in range(n-1):

for splitVal in set(dataSet[:,featIndex].T.tolist()[0]): mat0,mat1=self.binSplitDataSet(dataSet,featIndex,splitVal,self.features[featIndex][1])

if (np.shape(mat0)[0]<tolN) or (np.shape(mat1)[0]<tolN):

continue

p_l=(float)(np.shape(mat0)[0])/m

p_r=(float)(np.shape(mat1)[0])/m

phi=g-p_l*impurity(mat0)-p_r*impurity(mat1)

if phi>bestS:

bestIndex=featIndex

bestValue=splitVal

bestS=phi

mat0,mat1=self.binSplitDataSet(dataSet,bestIndex,bestValue,self.features[bestIndex][1])

if (np.shape(mat0)[0]<tolN) or (np.shape(mat1)[0]<tolN):

return None, leafType(dataSet)

return bestIndex, bestValue

＃递归建树

def createTree(self,dataSet, ops=(0.1,1)):

leafType=None

impurity=None

if self.targetType=="reg":

leafType=self.regLeaf

impurity=self.regErr

elif self.targetType=="cla":

leafType=self.claLeaf

impurity=self.GiniIndex

else:

raise Exception("illegal feature type exception!")

classList=[str(c) for c in dataSet[:,-1].T.tolist()[0]]

cases=np.shape(dataSet)[0]

feat,val=self.chooseBestSplit(dataSet, leafType, impurity, ops)

if feat==None: return (str(val),str(cases)+"/"+",".join(classList))

Tree={}

Tree["spInd"]=str(feat)

Tree["spVal"]=str(val) lSet,rSet=self.binSplitDataSet(dataSet,feat,val,self.features[feat][1])

Tree["spCasesLeft"]=str(np.shape(lSet)[0])

Tree["spCasesRight"]=str(np.shape(rSet)[0])

Tree["spClassListLeft"]=",".join([str(c) for c in lSet[:,-1].T.tolist()[0]])

Tree["spClassListRight"]=",".join([str(c) for c in rSet[:,-1].T.tolist()[0]])

Tree["left"]=self.createTree(lSet,ops)

Tree["right"]=self.createTree(rSet,ops)

return Tree

以上就是CART算法的基本思路，如果以CART为基树可以在其基础上构造随机森林。随机森林Random Forest的作者也就是CART之父Leo Breiman在其文章中声称rf不会产生过拟合overfitting, 这也是rf大受欢迎的原因之一。

首先，rf是一种组合学习算法，其本质是一类算法的统称，既遵循以下几个条件的：

模型包含一组决策树；
tree growing 有特定的生长机制：1.以CART做基树为例，树的生长如前所属，每个节点分裂后产生两个子节点；2.每棵基树生长的过程具有随机性，随机主要体现在a.随机选取训练样本；b.随机选取用于节点分裂的特征；
tree combination 树组合：树组合主要是指使用多棵基树模型来产生一个更可靠的最终结果，对于离散目标变量会使用投票的方式，对于连续型的目标变量对应会使用平均值；
self testing 自测试：每棵基树都随机选用部分训练样本进行建树，例如63%的原始训练样本，剩余的37%来计算oob（out of bag）错误率，因此整个过程有点类似cross-validation;
post-processing 后处理:rf引入了一个样本距离这个概念，如果两个样本越相似那么这两个样本就越容易落入同一个叶子节点，在基树个数很大的情况下，通过计算样本落在相同叶子节点的频率可以对样本进行相似度的计算，既对样本空间进行聚类；

Random Forest的算法步骤如下：

所需参数：

N: 基树的个数

features:特征描述

type：目标变量的数据类型，离散或连续

1.选取基树个数N，将特征空间和样本空间随机划分为N份；

子特征空间和子样本空间的随机挑选都遵循random with replacement，既不同的基树所分配的子特征空间和子样本空间可以有重叠；
子特征空间的大小一般为原始特征空间大小的平方根；
子样本空间的大小一般为原始样本空间大小的2/3，既0.67，另外1/3的样本用做oob测试；

2.根据CART算法训练N棵基树，对应使用1中随机生成的子特征空间和子样本空间；

每一棵基树的训练过程不需要剪枝pruning，因为随机的引入已经在最大程度上保证了不会产生过拟合；

3.计算oob error，对每一棵基树进行out of bag测试；

4.对新的待分类样本，分别使用N棵基树进行输出，汇总输出结果。

代码实现(Python):

＃首先引入相关模块，上面的CART实现将作为基树模块来使用

import math

import CART

import random

import C45

import numpy as np

import operator

＃初始化算法参数，N为基树的个数，features为原始特征空间，subFeature为子空间的大小，可以取原特征空间大小的平方根也可以人为指定

class randomForest:

def__init__(self,N,features,target_type,uniqueDiscValue,subFeature=0):

self.N=N

self.features=features

self.type=target_type

self.uniqueDiscValue=uniqueDiscValue

self.N_feat=subFeature

＃将样本空间和特征空间随机采样为N个子空间，一一对应

'''split data into N random samples'''

def randomSplit(self,dataSet):

'''will return both N-sample list and feature subspace'''

N_list=[]

subFeatures_list=[]

for l in range(self.N):

'''random feature subspace'''

f=self.features[:]

subFeatures=[]

for i in range(self.N_feat):

v=random.choice(f)

subFeatures.append(v)

f.remove(v)

'''实际上这里的序号和原始self.features里的序号是一致的。same oder with original feature space'''

subFeatures_idx=[self.features.index(i) for i in self.features if i in subFeatures]

'''random sample with replacement'''

tt=C45.splitTT(dataSet, 0.67)

subdataset=([],[])

'''train boosTrap'''

for i in tt[0]:

row=dataSet[i]

train_row=[row[f_idx] for f_idx in range(len(row)) if f_idx in subFeatures_idx]

train_row.append(row[-1])

subdataset[0].append(train_row)

'''test dataSet left out'''

for i in tt[1]:

test_row=dataSet[i]

subdataset[1].append(test_row)

N_list.append(subdataset)

subFeatures_list.append((subFeatures_idx,subFeatures))

‘’'返回格式为：(N_list[(train,test)],subFeatures_list[([subFeatures_idx],[subFeature])])'''

return (N_list,subFeatures_list)

＃随机森林训练，生成N棵基树

def trainForest(self,N_list,subFeatures):

'''using CART without pruning to train, return N-tree list'''

forest=[]

for i in range(self.N):

d=N_list[i][0]

f=subFeatures[i][1]

f_idx=subFeatures[i][0]

dataSet=np.mat(d)

dt=CART.CART(self.type,f)

dt.uniqueDiscValue=self.uniqueDiscValue

'''generate unique discrete feature values of subFeatures, for the use of substitute process since the index of sub-features is different with original feature space'''

for idx in range(len(f_idx)):

dt.featurUniqueDiscValue[idx]=dt.uniqueDiscValue[f_idx[idx]]

tree=dt.createTree(dataSet, ops=(0.1,1))

newTree=dt.substitute(tree)

forest.append(newTree)

return forest

#对每一个基树，计算oob错误率

def accuracy(self,test,tree):

oob_error=0

for testVec in test:

t=[self.uniqueDiscValue[i][testVec[i]] for i in range(len(testVec))]

predictedClass=self.classify(tree, testVec)

if predictedClass!=t[-1]:

oob_error+=1

return float(oob_error)/len(test)

＃投票产生最终分类结果（仅针对目标变量为离散的分类问题）

def forestClassify(self,forest,testVec):

'''will return the majority votes'''

votes=[]

for i in range(self.N):

r=self.classify(forest[i], testVec)

t=[self.uniqueDiscValue[j][testVec[j]] for j in range(len(testVec))]

votes.append(r)

bestClass=self.majorityCnt(votes)

return bestClass

关于基树个数的选择：

基树个数的设定一直都是rf研究的一个点，在阅读了一些资料后也提出几个粗浅的认识供参考：

理论上基树的个数越多，组合学习的准确率就越高，当基树个数增加到一定数字时性能的提升会越来越小而训练的代价会越来越大，这个时候就应该适时停止增加基树的个数从而保证performance/cost之间的平衡；
基树的个数和特征空间的大小成正比；
基树的个数和样本空间的大小成正比；

关于rf不会过拟合的说法：

在实际应用中，数据集往往存在不可预知的噪声，Mark R. Segal (April 14 2004. "Machine Learning Benchmarks and Random Forest Regression." Center for Bioinformatics & Molecular Biostatistics)在他的研究中发现在一些含有噪声的数据集中rf会过拟合！
因此更有必要将基树的个数作为参数，记录performance/cost之间的tradeoff

登录查看更多