【2023新书】解释模型分析:探索、解释和检验预测模型，327页pdf

2023 年 4 月 10 日 专知

解释模型分析探索、解释和检查预测模型是一套方法和工具，旨在建立更好的预测模型，并监测其在不断变化的环境中的行为。今天，预测建模的真正瓶颈既不是缺乏数据，也不是缺乏计算能力，也不是不充分的算法，也不是缺乏灵活的模型。它是缺乏模型探索(提取模型学习到的关系)、模型解释(理解影响模型决策的关键因素)和模型检查(识别模型弱点和评估模型性能)的工具。本书介绍了一系列与模型无关的方法，可用于任何黑盒模型以及分类和回归问题的实际应用。

https://www.routledge.com/Explanatory-Model-Analysis-Explore-Explain-and-Examine-Predictive-Models/Biecek-Burzykowski/p/book/9780367693923#:~:text=Explanatory%20Model%20Analysis%20Explore%2C%20Explain%20and%20Examine%20Predictive%20Models%20is,behaviour%20in%20a%20changing%20environment.

预测模型用于根据某个感兴趣变量的值来猜测(统计学家称之为预测)某个感兴趣变量的值。例如，基于历史数据的销量预测，基于患者特征的心脏病风险预测，基于Facebook评论的政治态度预测。预测模型在整个人类历史中都被使用。例如，古埃及人利用对天狼星上升的观察来预测尼罗河的洪水。两个多世纪前，勒让德(Legendre)和高斯(Gauss)分别于1805年和1809年发表了一种更严格的模型构造方法——最小二乘法。随着时间的推移，在经济学、医学、生物学和农业方面的应用数量不断增加。回归(regression)这个词是由Francis Galton于1886年提出的。最初，它指的是生物应用，而今天它被用于各种允许预测连续变量的模型。名义变量的预测被称为分类，它的开始可以归因于罗纳德·费雪(Ronald Fisher)在1936年的工作。

在上个世纪，已经开发了许多可用于预测目的的统计模型。这些模型包括线性模型、广义线性模型、分类和回归树、基于规则的模型等。在我们已经进入的“大数据”时代，个人计算机计算能力的增强和大数据集的可用性推动了预测模型的数学基础的发展。随着人们对预测模型需求的不断增长，模型的灵活性、内变量选择或特征工程能力以及预测的高精度成为人们关注的焦点。为了获得鲁棒的模型，使用模型的集成。bagging、boosting或model stacking等技术将数百或数千个更简单的模型组合成一个超级模型。大型深度神经模型可能有超过10亿个参数。

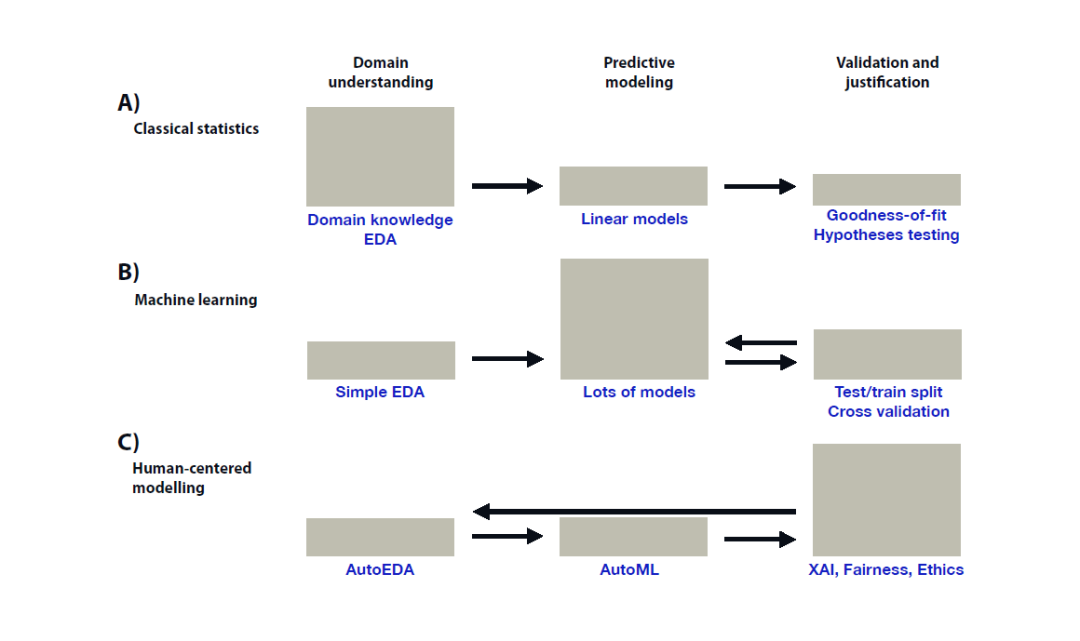
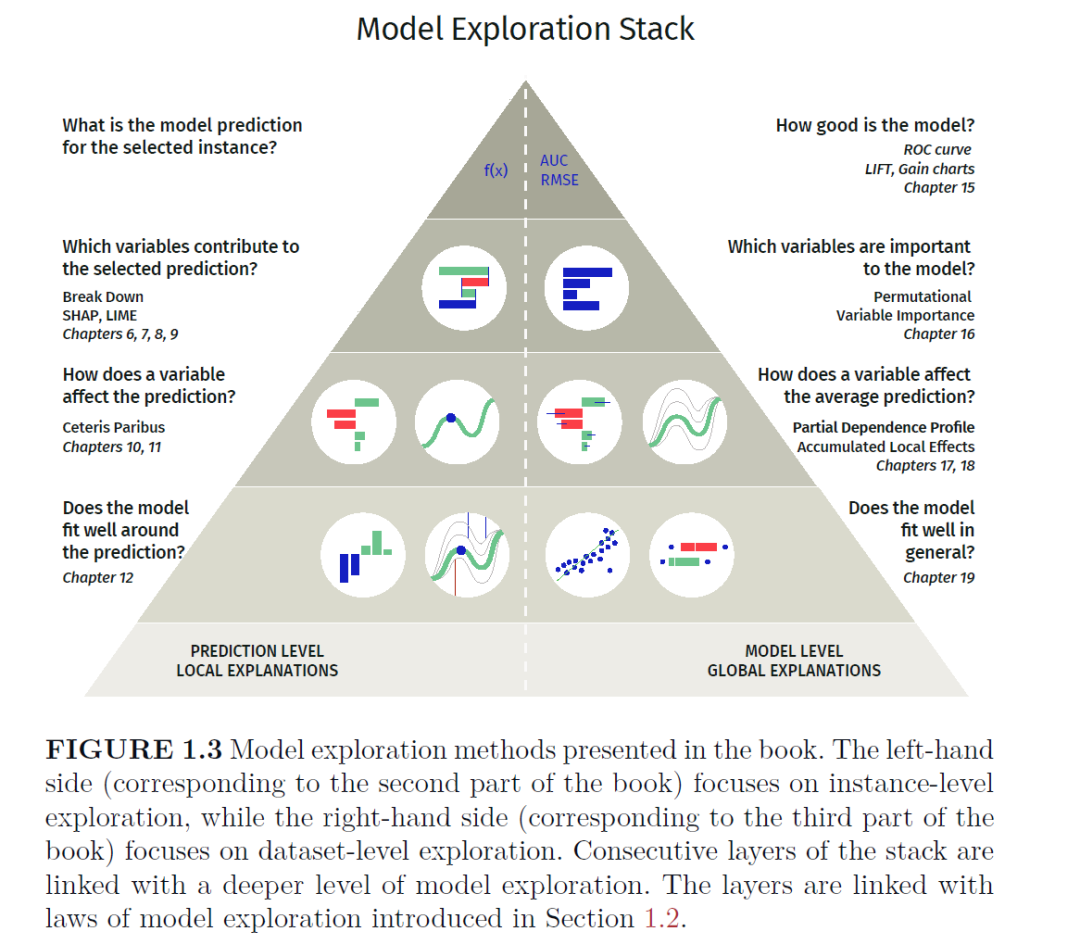
这本书分为四个主要部分。在第一部分的引言中，我们介绍本书中使用的符号、数据集和模型。在第二部分，实例级探索中，我们介绍了探索和解释模型对单个观察的预测的技术。在第三部分，数据集级别的探索，我们将介绍探索和解释整个数据集的模型的技术。在第四部分，用例中，我们将前几部分中介绍的方法应用于一个想要评估足球运动员价值的例子。第二部分和第三部分的结构如图1 - 3所示。本书第一部分由第2 ~ 4章组成。在第2章中，我们将简要介绍数据探索和模型构建的过程，以及后续章节中使用的关键概念的表示法和定义。此外，在第3.1章和第3.2章中，我们会简要介绍R和Python的工具和包，这些工具和包是实现本书结果所必需的。最后，在第4章中，我们会介绍两个数据集，这两个数据集贯穿全书，用来说明本书介绍的方法和工具。

本书第二部分的重点是实例级的解释器，由第6 ~ 13章组成。第6-8章介绍了将模型的预测分解为每个解释变量对应的贡献值的方法。特别地，第6章介绍了预测模型的加法属性分解(BD)方法，而第7章将该方法扩展到包含交互的属性。第8章描述了Shapley加性解释(SHAP) (Lundberg和Lee, 2017)，这是一种分解模型预测的替代方法，与Shapley值密切相关，最初由Shapley(1953)为合作博弈开发。第9章将介绍另一种解释单实例预测的方法。它是基于一个更简单的玻璃盒模型的黑盒模型的局部近似。在本章中，我们将讨论局部可解释的模型无关解释(LIME)方法(Ribeiro等人，2016)。这几章对应于图1 - 3所示的栈的第二层。

在第10-12章中，我们将介绍基于CP (ceteris-paribus)概要的方法。图中展示了由10引起的基于模型预测的变化，而第11章展示了基于cp -profile的度量，总结了选定变量对模型预测的影响。该测度可用于确定模型探索中变量的顺序。对于具有大量解释变量的模型来说，这一点尤为重要。第12章重点介绍模型诊断。它描述了局部稳定性图，对研究某个特定的单一观测的不良预测的来源很有用。第二部分的最后一章(第13章)比较了实例级探索的各种方法。第三部分由第14 ~ 19章组成，侧重于数据集层面的探索。这几章介绍方法的顺序与图1 - 3中右侧的顺序相同。第15章特别介绍了用于评估预测模型整体性能的方法。第16章介绍了评估解释变量重要性的有用方法。第17章和第18章介绍了探索变量效应的单变量部分依赖和累积依赖方法。这些方法对应图1 - 3所示的栈右侧的第三层(从最上面算起)。这一部分的最后一章是第19章，总结了基于模型残差的诊断技术。本书在第21章结束，介绍了一个模型开发过程的例子，在这个例子中，我们应用了本书第二部分和第三部分讨论的所有方法。

专知便捷查看