【2023新书】机器学习集成方法，354页pdf

现在是学习集成方法的最佳时机。本书介绍的模型主要分为三类。 https://www.manning.com/books/ensemble-methods-for-machine-learning

基础集成方法——每个人都听说过的经典方法，包括历史集成技术，如bagging、随机森林和AdaBoost * 最先进的集成方法——现代集成时代经过试验和测试的强大工具，它们构成了许多现实世界中生产中的预测、推荐和搜索系统的核心 * 新兴的集成方法-最新的方法的研究代工厂处理新的需求和新兴的优先级，如可解释性

每一章将介绍一种不同的集成技术，使用三管齐下的方法。首先，你将通过逐步可视化学习实际是如何进行的，了解每种集成方法背后的直觉。其次，你将自己实现每个集成方法的基本版本，以完全理解算法的具体细节。第三，你将学习如何实际应用强大的集成库和工具。 大多数章节都有自己的案例研究，这些案例来自手写数字预测、推荐系统、情感分析、需求预测等应用。这些案例研究在适当的情况下解决了几个现实世界的问题，包括预处理和特征工程，超参数选择，高效的训练技术和有效的模型评估。 本书分为三部分，共九章。第1部分是集成方法的简单介绍，第2部分介绍并解释了几个基本的集成方法，第3部分涵盖了高级主题。 第1部分，“集成的基础”，介绍集成方法以及为什么你应该关注它们。这一部分还包含本书其余部分将介绍的集成方法的路线图。 第1章讨论了集成方法和基本的集成术语。它还引入了适应性与复杂性的权衡(或者更正式的叫法是偏差-方差权衡)。你将在本章中构建第一个集成。 第2部分，“基本集成方法”，介绍了几个重要的集成方法族，其中许多被认为是“基本的”，在现实世界的应用中广泛使用。在每一章中，你都将学习如何从零开始实现不同的集成方法，它们的工作原理，以及如何将它们应用于实际问题。

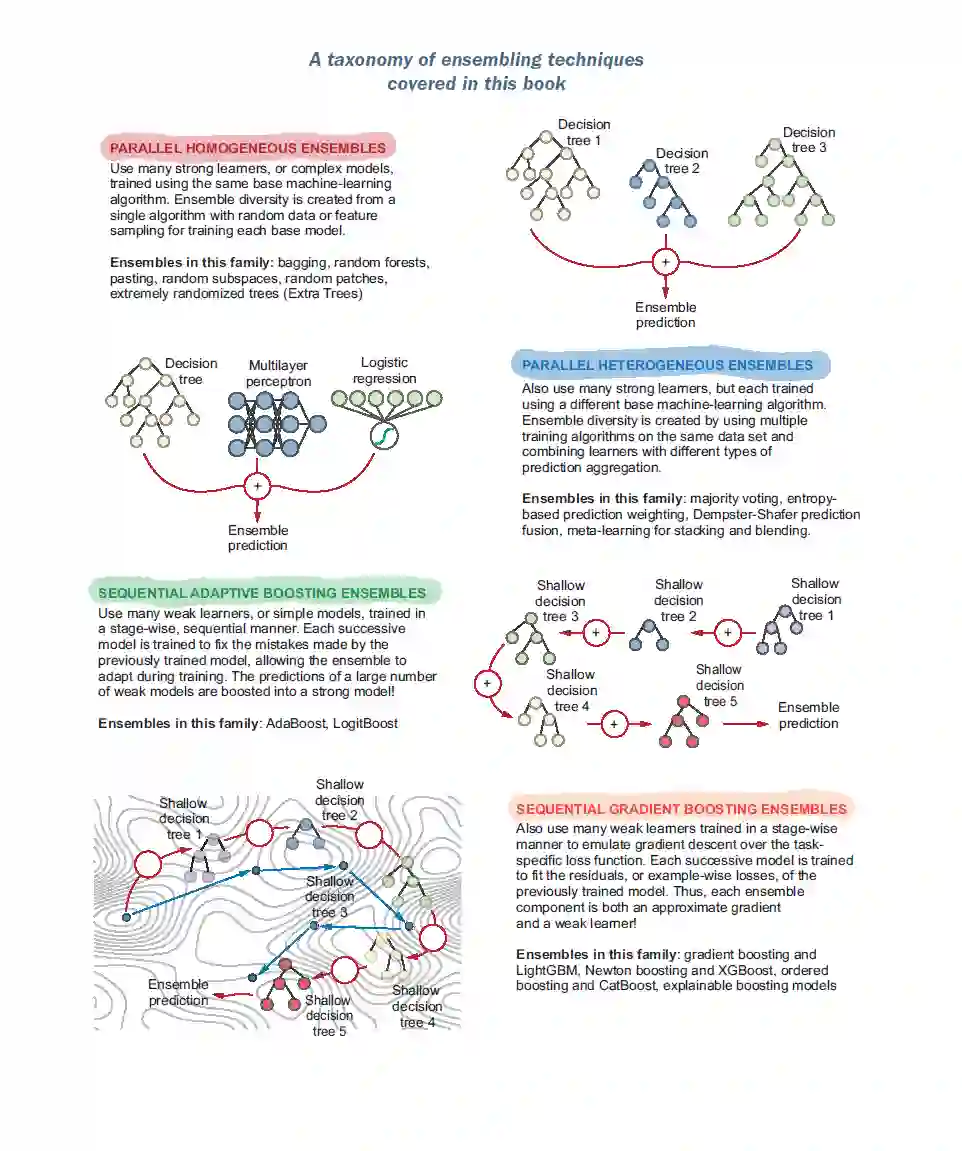
第2章开始我们的旅程，平行集成方法，特别是平行同质集成。集成方法包括bagging、随机森林、粘贴、随机子空间、随机补丁和额外的树。 第3章继续介绍更多并行集成，但本章的重点是并行异构集成。介绍的集成方法包括通过多数投票组合基础模型、通过加权组合、使用Dempster-Shafer进行预测融合以及通过堆叠进行元学习。 第4章介绍了另一类集成方法——顺序自适应集成——特别是将许多弱模型提升为一个强大模型的基本概念。介绍的集成方法包括Ada- Boost和LogitBoost。 第5章建立在boosting的基本概念之上，并涵盖了另一种基本的序列集成方法，梯度boosting，它将梯度下降与boosting相结合。本章将讨论如何使用scikit-learn和LightGBM训练梯度增强集成。 第6章继续探索牛顿boosting的序列集成方法，牛顿boosting是梯度boosting的有效扩展，结合了牛顿下降和boosting。本章将讨论如何使用XGBoost训练Newton boosting集合。 第3部分“实际应用中的集成:使集成方法适用于数据”向您展示了如何将集成方法应用于许多场景，包括具有连续和计数型标签的数据集以及具有分类特征的数据集。你还将学习如何解释集合以及它们的预测: 第7章展示了我们如何为不同类型的回归问题和广义线性模型训练集成，其中训练标签是连续的或计数的。本章涵盖了线性回归、泊松回归、伽马回归和Tweedie回归的并行和顺序集成。 第8章确定了使用非数值特征学习的挑战，特别是分类特征，以及将帮助我们为此类数据训练有效集成的编码方案。本章还讨论了两个重要的实际问题:数据泄漏和预测偏移。最后，我们将看到如何使用ordered boosting和CatBoost克服这些问题。 第9章从集成方法的角度涵盖了新兴的非常重要的主题可解释人工智能。本章将介绍可解释性的概念以及它的重要性。还讨论了几种常见的黑盒可解释性方法，包括排列特征重要性、部分依赖图、代理方法、局部可解释的模型无关解释、Shapley值和Shapley加性解释。介绍了玻璃盒集成方法、可解释增强机和InterpretML包。 结语以其他主题结束我们的旅程，以供进一步探索和阅读。