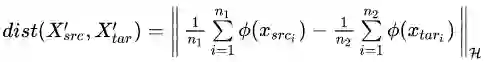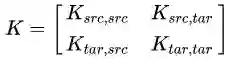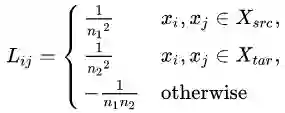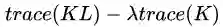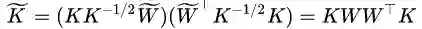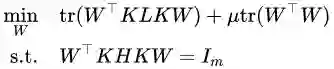迁移成分分析 (TCA) 方法简介

2017 年 9 月 15 日 AI研习社 王晋东

本文原作者王晋东不在家，本文原载于知乎专栏——机器有颗玻璃心。AI 研习社已获得转载授权。王晋东 (不在家)，中国科学院计算技术研究所博士生，目前研究方向为机器学习、迁移学习、人工智能等。

之前整理总结迁移学习资料的时候有网友评论，大意就是现在的类似资料大全的东西已经太多了，想更深入地了解特定的细节。从这篇文章开始我将以《小王爱迁移》为名写一系列的介绍分析性的文章，与大家共享迁移学习中的代表性方法、理论与自己的感想。由于我的水平有限，请各位多多提意见，我们一起进步。今天第一篇必须以我最喜爱的杨强老师的代表性方法 TCA 为主题！（我的第一篇文章也是基于 TCA 做的）

【我刚整理重写好的加速版 TCA 代码（matlab）：http://t.cn/RazheBv】

问题背景

机器学习中有一类非常有效的方法叫做降维（dimensionality reduction），用简单的话来说就是，把原来很高维度的数据（比如数据有 1000 多列）用很少的一些代表性维度来表示（比如 1000 多维用 100 维来表示）而不丢失关键的数据信息。这些降维方法多种多样，比如：主成分分析（PCA，principal component analysis）、局部线性嵌入（LLE,locally linear embedding）、拉普拉斯特征映射（Laplacian eigen-map）等。这些方法的过程大体都是一个大的矩阵作为输入，然后输出一个小矩阵。那么在迁移学习中，有没有这样的方法，通过降维来达到数据维度减少，而且能达到迁移学习目的呢？答案是显然的，就是我们要说的迁移成分分析（TCA，transfer component analysis）。看，名字就跟 PCA 很像。

TCA 最早是由香港科技大学杨强教授团队提出，首次出现在 AAAI-09 上，后来整理丰富成了一篇期刊文章，发表在 11 年的 IEEE Trans. Neural Network（现在这个期刊名字后面多了 and Learning System）上。这个方法是迁移学习领域经典性的文章，从 2011 年到现在接近 6 年过去，在 Google scholar 上引用量为 569 次，并且在持续增长。

简介

TCA 属于基于特征的迁移学习方法。那么，它做了一件什么事呢？用通俗的语言来说，跟 PCA 很像：PCA 是一个大矩阵进去，一个小矩阵出来，TCA 呢，是两个大矩阵进去，两个小矩阵出来。从学术角度讲，TCA 针对 domain adaptation 问题中，源域和目标域处于不同数据分布时，将两个领域的数据一起映射到一个高维的再生核希尔伯特空间。在此空间中，最小化源和目标的数据距离，同时最大程度地保留它们各自的内部属性。直观地理解就是，在现在这个维度上不好最小化它们的距离，那么我就找个映射，在映射后的空间上让它们最接近，那么我不就可以进行分类了吗？

我一直强调，任何问题都要看它的本质，TCA 本质是什么呢？完成迁移学习的要求。迁移学习的要求是什么呢？让源域和目标域距离尽可能小呗。

方法

有许多种方法都在试图减小源域和目标域的距离，那么，TCA 的贡献在哪里？以我的理解，TCA 将这个计算距离的方法变得通用而简单，这就是它最大的贡献。下面我以自己的理解介绍 TCA 方法的基本流程。

假设

任何方法都基于一定的假设。胡适说过，大胆假设，小心求证。但是他那个时候没有计算机，我们搞计算机的人则是，大胆假设，更大胆求证。为啥？我们就算失败了也没有什么嘛，最多把电脑搞崩溃了我再重装系统么。所以，搞学术一定不要怕假设。假设是学术成功的基石呢！

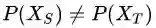
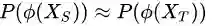
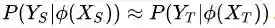
TCA 的假设是什么呢？很简单：源域和目标域的边缘分布是不一样的，也就是说，，所以不能直接用传统的机器学习方法。但是呢，TCA 假设存在一个特征映射 $\phi$，使得映射后数据的分布，更进一步，条件分布。这不就行了么。好了，我们现在的目标是，找到这个合适的 $\phi$，一作映射，这事就解决了。

具体

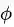
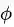
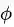
但是世界上有无穷个这样的，也许终我们一生也无法找到这样的。庄子说过，吾生也有涯，而知也无涯，以有涯随无涯，殆已！我们肯定不能通过穷举的方法来找的。那么怎么办呢？

回到迁移学习的本质上来：最小化源域和目标域的距离。好了，我们能不能先假设这个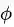是已知的，然后去求距离，看看能推出什么呢？

更进一步，这个距离怎么算？世界上有好多距离，从欧氏距离到马氏距离，从曼哈顿距离到余弦相似度，我们需要什么距离呢？TCA 利用了一个经典的也算是比较 “高端” 的距离叫做最大均值差异（MMD，maximum mean discrepancy）。这个距离的公式如下：

看着很高端（实际上也很高端）。MMD 是做了一件什么事呢？简单，就是求映射后源域和目标域的均值之差嘛。

事情到这里似乎也没什么进展：我们想求的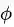仍然没法求。

TCA 是怎么做的呢，这里就要感谢矩阵了！我们发现，上面这个 MMD 距离平方展开后，有二次项乘积的部分！那么，联系在 SVM 中学过的核函数，把一个难求的映射以核函数的形式来求，不就可以了？于是，TCA 引入了一个核矩阵：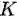

以及:

这样的好处是，直接把那个难求的距离，变换成了下面的形式：

trace 是矩阵的迹，用人话来说就是一个矩阵对角线元素的和。这样是不是感觉离目标又进了一步呢？

其实这个问题到这里就已经是可解的了，也就是说，属于计算机的部分已经做完了。只不过它是一个数学中的半定规划（SDP，semi-definite programming）的问题，解决起来非常耗费时间。由于 TCA 的第一作者 Sinno Jialin Pan 以前是中山大学的数学硕士，他想用更简单的方法来解决。他是怎么做的呢？

他想出了用降维的方法去构造结果。

这里的 W 矩阵是比 K 更低维度的矩阵。最后的 W 就是问题的解答了！

求解

好了，问题到这里，整理一下，TCA 最后的优化目标是：

这里的 $H$ 是一个中心矩阵，.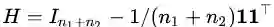

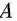
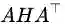
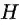
这个式子下面的条件是什么意思呢？那个 min 的目标我们大概理解，就是要最小化源域和目标域的距离，加上 W 的约束让它不能太复杂。那么下面的条件是什么呢？下面的条件就是要实现第二个目标：维持各自的数据特征。TCA 要维持的是什么特征呢？文章中说是 variance，但是实际是 scatter matrix，就是数据的散度。就是说，一个矩阵散度怎么计算？对于一个矩阵，它的 scatter matrix 就是。这个就是上面的中心矩阵啦。

解决上面的优化问题时，作者又求了它的拉格朗日对偶。最后得出结论，W 的解就是的前 m 个特征值！简单不？数学美不美？然而，我是想不出的呀！

小结

好了，我们现在总结一下 TCA 方法的步骤。输入是两个特征矩阵，我们首先计算 L 和 H 矩阵，然后选择一些常用的核函数进行映射（比如线性核、高斯核）计算 K，接着求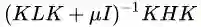的前 m 个特征值。仅此而已哦。然后，得到的就是源域和目标域的降维后的数据，我们就可以在上面用传统机器学习方法了。

总结

怎么样，到此为止我们把 TCA 方法介绍完了。我们回顾一下，它的最核心工作是什么呢？我认为有两点：一是把问题转化成数学问题转化得很彻底；二是最优化求解方法很厉害。我们能从中学习什么呢？求解问题的方法感觉是学不来了，我们又不是数学出身。我们只能照猫画虎，学习人家对问题的转化方式，怎么就能很好地把一个问题转化成数学表示？这也是机器学习和人工智能相关方向研究生最重要的能力！关于 TCA 的 Python 和 Matlab 代码可以参考我的 Github：https://github.com/jindongwang/transferlearning。

最后说一个 TCA 的优缺点。优点是实现简单，方法本身没有太多的限制，就跟 PCA 一样很好用。缺点就是，尽管它绕开了 SDP 问题求解，然而对于大矩阵还是需要很多计算时间。主要消耗时间的操作是，最后那个伪逆的求解以及特征值分解。在我的电脑上（i7-4790CPU+24GB 内存）跑 2000*2000 的核矩阵时间大概是 20 秒。

References

[1] TCA 原版文章：S. J. Pan, I. W. Tsang, J. T. Kwok and Q. Yang, "Domain Adaptation via Transfer Component Analysis," in IEEE Transactions on Neural Networks, vol. 22, no. 2, pp. 199-210, Feb. 2011.doi: 10.1109/TNN.2010.2091281

[2] Scatter matrix: Scatter matrix | Wikiwand（http://t.cn/RpQjLo0）